- HOME
- 『問題解決力を鍛える！アルゴリズムとデータ構造』出版記念講演会
2020年10月13日 18:00
2020/11/05 17:00 追記
出版記念講演会はご好評のうちに終了しました。アンケートでご要望の多かった動的計画法に関する内容など、本講演の続編の開催を検討中です。乞うご期待！
アルゴリズム本、出しました！
NTTデータ数理システムでアルゴリズムの探究をしている大槻です。このたび、今話題のアルゴリズムについて、丁寧に解説した書籍を上梓させていただくことになりました！
私はこれまで3年間にわたって、プログラマのための情報共有サービスである Qiita にて、アルゴリズムの面白さを伝える記事を多数投稿してきました。本書は、これらの記事を有機的にまとめ上げ、さらに多数のトピックを追加したものとなっています。
- アルゴリズムとは何か！？
- 計算量オーダーの求め方を総整理！
- 動的計画法超入門！
- 再帰関数を学ぶと、どんな世界が広がるか
- スタックとキューを極める！
- ソートを極める！
- DFS（深さ優先探索）超入門！
- 実世界で超頻出！二部マッチングの解法を総整理！
出版記念講演会、やります！
NTTデータ数理システムでは、アルゴリズム書籍出版を記念して、講演会を開催することを決定いたしました。拙著に込めたメッセージとともに、現代社会を生き抜くためにアルゴリズムを学ぶ意義や、アルゴリズムの面白さについてお伝えできればと思います。
日時
出版記念講演会は終了しました。
2020/10/29（木） 15:00-16:00
場所
- 会場(20名まで)
株式会社NTTデータ数理システム セミナールーム（信濃町）
https://www.msi.co.jp/company/location.html - 同時配信
Zoom Webinar
講演概要
本講演では、アルゴリズム本出版を記念して、問題解決のためのアルゴリズム的思考法についてお話しします。
近年、小学校におけるプログラミング教育の必修化などの改革もあり、アルゴリズム的思考（プログラミング的思考）の重要性が広く認識されてきています。アルゴリズムを学ぶことで身に付く問題解決力は、プログラミングを仕事としている方はもちろん、あらゆる方にとって役立つものといえます。また、アルゴリズムを考えることは、パズルのように楽しいものでもあります。楽しみながら試行錯誤することが、問題解決力を伸ばす有効な方法といえるでしょう。
拙著『問題解決力を鍛える！アルゴリズムとデータ構造』では、刺激的で楽しい問題を多数解説しました。本講演では、それらの問題の舞台裏についても紹介していきます。アルゴリズム的思考の果たす役割、楽しさについてお伝えできればと思います。
参加申込
出版記念講演会は終了しました。
- 2020/10/29（木）15:00-16:00：講演会場
- 2020/10/29（木）15:00-16:00：Webinar
※申し込むをクリックすると、当社が契約する株式会社パイプドビッツの情報管理システム「スパイラル」のページへリンクします。
注意事項
感染症拡大を避けるため、講演会場でご参加いただく方には以下のお願いをいたします。
- 会場入り口での検温（体温が37.5℃以上の方は入場をお断りします）
- 会場入場時の手指消毒
- 会場内でのマスクの着用（マスクはご自身でご用意ください）
上記およびその他の理由で感染症拡大防止にご協力いただけないと会場スタッフが判断した場合には、ご退場いただく場合があります。あらかじめご了承ください。
なぜ、アルゴリズムか
現代社会では至るところで AI という言葉を耳にするようになりました。それに関連して「アルゴリズム」という言葉を聞いたことのある方も多いでしょう。しかし、そもそもアルゴリズムとはなんでしょうか？それを学ぶことにどんな意味があるのでしょうか？講演会では、それらの疑問にお答えいたします。ここでは簡単に、アルゴリズムを学ぶ意義をいくつか紹介します。
アルゴリズムは「問題解決の道具」
まず、アルゴリズムとは問題解決のための手順のことです。世の中には解決すべき問題がたくさんあります。アルゴリズム的思考法は、AI やデータサイエンスをはじめとして、マーケティング、広告、製造業、シフトスケジューリング、金融、そして日常生活に至るまで、あらゆる分野で横断的に活躍するものです。
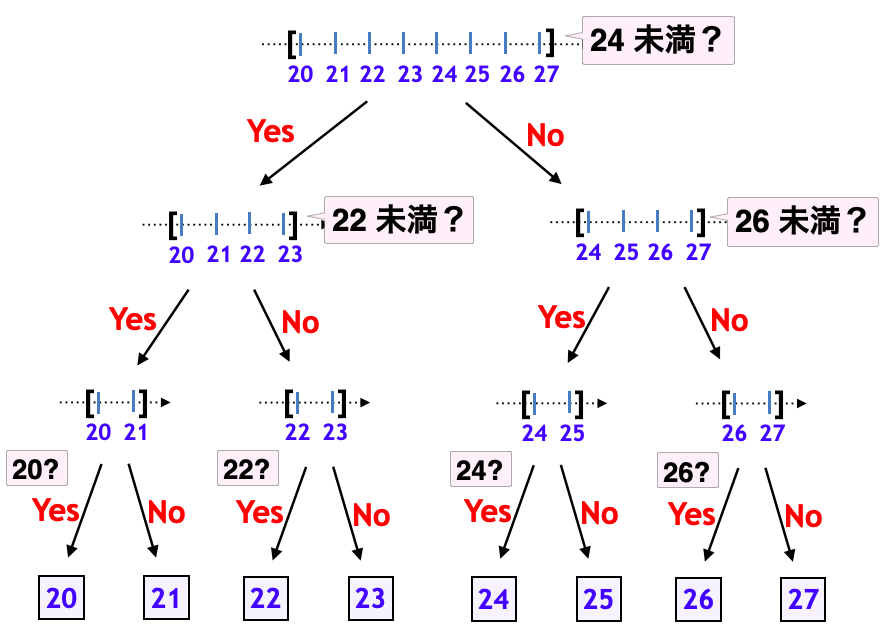
一例として「二分探索法」と呼ばれるアルゴリズムを取り上げてみましょう。まずは日常的な問題（数当てゲーム）から考えてみます。A さんに「20以上28未満の数」を一つ思い浮かべてもらいます。あなたは今から A さんに「Yes / No で答えられる質問」を3回だけ行います。それによって A さんの思い浮かべた数を当てることはできるでしょうか？
できるだけ効率よく選択肢を狭めていきたいところです。1回目の質問では「24未満ですか？」と聞いてみましょう。そうすると、
・ Yes の場合：A さんの思い浮かべた数は20以上24未満であると判明
・ No の場合： A さんの思い浮かべた数は24以上28未満であると判明
というふうになります。どちらの答えであったとしても、8通りあった選択肢が4通りに半減するのです。以下同様に、下図に示す手順によって、3回の質問で A さんの年齢を当てることができます。このように、選択肢を徐々に半減させていく方法を二分探索法と呼びます。
二分探索法はさまざまな分野で活躍します。たとえばプログラムの1〜200行目の間にバグがあることが判明した場合、100行目までが正常かどうかを判定することで、バグのある範囲を絞ることができます。
他にもスケジューリング問題への応用もあります。たとえば業務平準化の要望から「最も働いている人の月間労働時間を最小に抑えてください」という問題を解きたいとします。そして最も働いている人の労働時間が120〜180時間の範囲内であったとします。まずは「全員の労働時間を150時間以内に抑えることが可能かどうか」という問題を解いてみましょう。この答えが Yes であれば、全員の労働時間をさらに抑え込むことが可能かどうかを検討します。No であれば、制約を緩和することを検討します。
以上のように、選択肢を半減させていくという二分探索法は、さまざまな分野の問題の解決に活用できます。二分探索法だけではありません。アルゴリズムという分野では、幅広い分野の問題の解決に寄与する手法が多数開発されてきました。冒頭の書籍は、そのようなアルゴリズム設計技法を最大限に重視し、「活きた問題解決能力を身につけて欲しい」という願いを込めて執筆しました。
アルゴリズムを学ぶと世界が変わる
大袈裟な表現かもしれませんが、アルゴリズムを学ぶと世界の見え方が大きく変わります。筆者自身も、アルゴリズムを学ぶ以前は、問題を解決するという行為を、高校数学における「公式」のようなものを与えることである、というイメージでとらえていました。つまり、その問題に対する解を具体的に得ることが問題解決であるというイメージでした。しかしアルゴリズムを学んでからは、具体的な解を書き下すことができなくても、解を得るための「手順」を与えることができればよい、という見方ができるようになり、問題解決手段が大きく拡がったのです。
たとえば、現在駅から目的駅まで最短で行きたいとします。最短ルートが求められる公式は存在するでしょうか？もし、以下の「二次方程式の解の公式」のような公式が存在して、現在駅と目的駅を代入すれば答えが出てくるならば、とても便利です。
[[x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}]]
現実はそこまで甘くはありません。このような公式があるとはとても思えません。しかし、最短ルートを導出するための「手順」を与えることはできるのです！公式に代入すれば一発とまでは行きませんが、手順に沿って計算すれば最短ルートを求めることができます（具体的な手順は本書の14章で解説しています）。手で計算するのは大変ですが、現代社会にはコンピュータがあります。
このように、アルゴリズム的思考法を身につけると、問題解決手段が大きく拡がります。しかもあらゆる分野で活用できるものです。アルゴリズム的思考法は AI や IoT といった分野の流行に依らない、一生モノのスキルとなります。
明快なロジックが考えられるようになる
多くの方にとって、この効果が最も重要かもしれません。アルゴリズムを設計するとは、「手順」を突き詰めることに他なりません。つまりアルゴリズムを学ぶと、単に知識が身に付くだけではなく、手順・ロジックを明快かつシンプルにする能力が磨かれるのです。手順をシンプル化することは、プログラミングの手間を減らすだけでなく、余計なバグを混入させるリスクも軽減できます。
近年、AtCoder などを中心として開催されているプログラミングコンテストによって、アルゴリズム人材の価値が急速に認識されてきています。その理由は、単にアルゴリズム知識が豊富な人材が必要とされているだけでなく、明快なロジックを考案する能力が重宝されていると言えるでしょう。
書籍出版記念講演に向けて
本書を執筆するにあたっては、1つの信念がありました。それは「アルゴリズムは実際の問題の解決に活かしてナンボである」ということです。クイックソートといった、既存のアルゴリズムをわかりやすく解説するのみに終始せず、アルゴリズムの組み立てのもとになっている数理をしっかりと解説し、動的計画法などのアルゴリズム技法を詳しく解説するように試みました。それによって、上に述べたような「生きた問題解決能力」を身につけていただけたならば、大きな喜びです。
本講演では、アルゴリズム的思考法について、さらに掘り下げた内容をお話します。ここまで「問題解決のための道具」などと言ってきましたが、結局はアルゴリズムは楽しいと思っていただけたら望外の喜びです。
