逆問題解析とは
通常のシミュレーションは、「支配方程式」と「種々の条件」から「応答」を求めるものです。
この際に課す条件には、初期条件、境界条件、負荷があります。例えば、熱伝導シミュレーションでは、構造体内部に熱源を設定した上(負荷)で熱伝導方程式を解き、構造体表面の温度分布(応答)を得ることができます。
その一方で、あらかじめ「応答」が分かっていて、それから「支配方程式」や「種々の条件」を求めたい場合もあります。
例えば、構造体表面の温度分布が観測データとして取得できていて(応答)、それから構造体内部のどの位置に熱源があるのか(負荷)を特定する問題があります。
このような問題は、通常のシミュレーションとは入力と出力が逆になっており、逆問題解析と呼ばれます。逆問題解析は、熱源特定の他にも、非破壊検査、最適形状作成、最適制御にも適用できます。
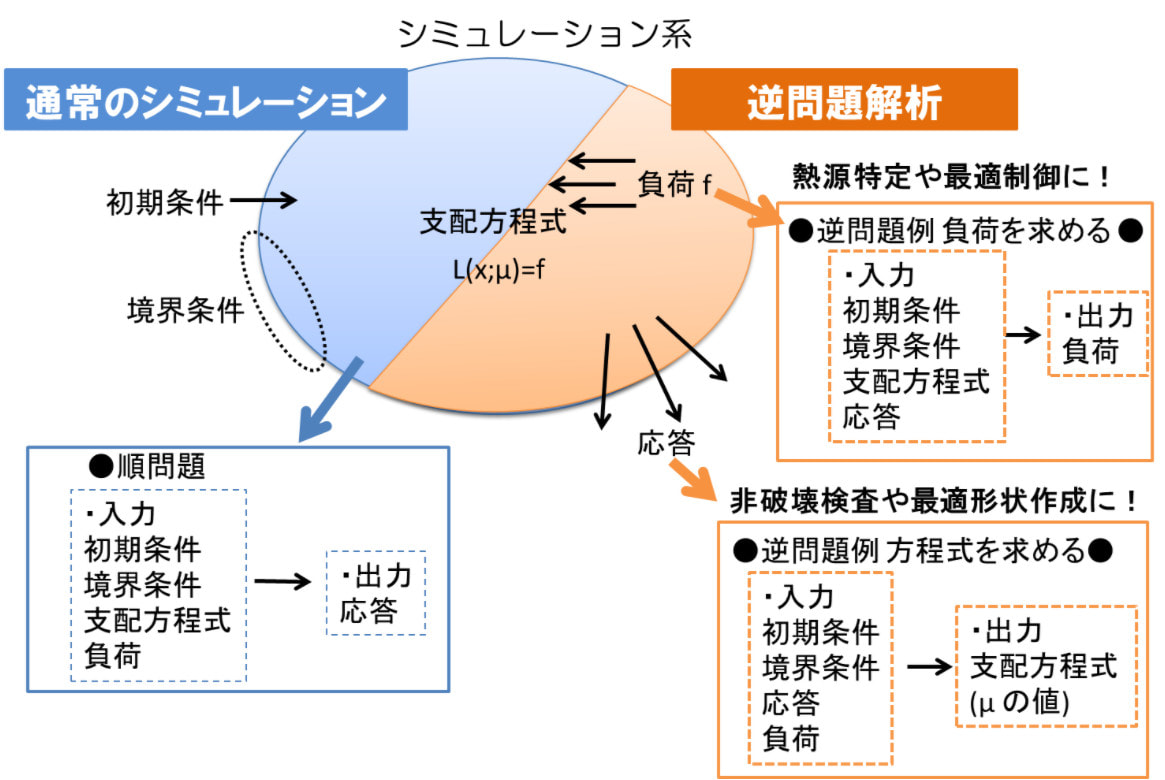
逆問題解析と通常のシミュレーションの違い
最適化を用いた逆問題解析
逆問題解析の実現方法の一つとして、「最適化アルゴリズム」と「シミュレーション技術」を連携させる方法があります。
従来の取り扱いでは、「最適化ソルバ」と「シミュレータ」の間でデータのやり取りを行うことで求解を行っていました。
しかしながら、昨今、偏微分方程式制約付き最適化(PDE constrained optimization、PCO)という枠組みが提案されるようになり、「最適化ソルバ」が「シミュレータ」を取り込む形に拡張できるようになりました。
このような手法は all at once 法と呼ばれます。一方で、従来の取り扱いは、black box 法と呼ばれます。
- all at once 法
「最適化ソルバ」が「シミュレータ」を取り込む形で実現され、両方の計算が一括して行われます。
シミュレータに手を入れることが出来るため、様々な問題に対して、柔軟な対応が可能です。
- black box 法
「最適化ソルバ」と「シミュレータ」が独立で、それらの間でデータのやり取りを行うことで求解します。
既存のシミュレータをそのまま使うことができます。
当社には、各種の最適化アルゴリズムを備えた汎用ツール、およびシミュレーションの豊富な実績がありますので、どちらの方法にも対応できます。
お客様が解かれたい問題を分析した上で,その特性にあった手法をご提案致します。
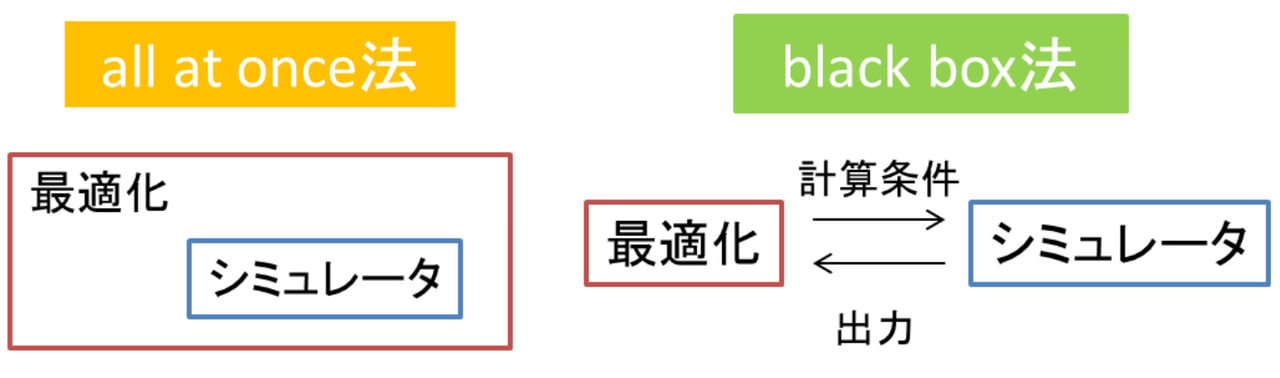
最適化アルゴリズムとシミュレーションの連携手法
all at once 法
従来より用いられてきた black-box 法では、既存のシミュレータをそのまま使える反面、問題によっては計算時間に課題がありました。この点に対処できるのが、all at once 法です。
この手法では、離散化された支配方程式が制約に加わり、パラメータと物理量を同時に解きます。
そのため、(black box 法では扱われることのない)物理的に意味のない領域まで経路を広げることや、問題の構造を考慮した解法を用いることで、black box 法より早く最適解を求めることができます。
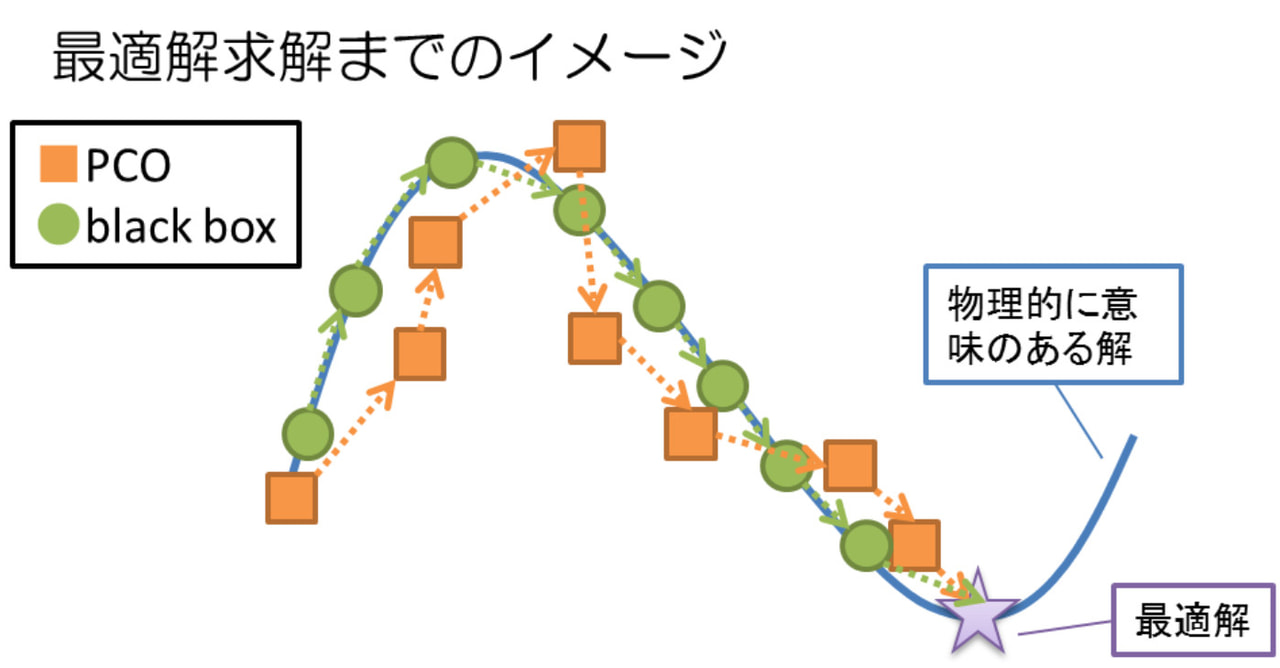
all at once 法の利点
black box 法
black box 法は、シミュレーション中の変数(順問題変数)とシミュレーション中のパラメータ(逆問題変数)を交互に変化させる手法です。
通常、商用シミュレータの詳細な実装内容は明らかではありません。black box 法の中には、このようなシミュレータに対しても適用できる手法もあります。
この場合、「最適化ソルバ」と「シミュレータ」が独立で、それらの間でデータのやり取りを行うことで求解します。
最適化を行うには目的関数を与える必要があります。しかし、シミュレータがブラックボックスであれば、目的関数の数式表現(目的関数の微分値等の取得)は困難です。
このような場合に用いられる最適化アルゴリズムの一つに、Derivative Free Optimization(DFO)があります。
モデル関数の構築
逆問題解析の事例
[ all at once 法]表面データを用いた内部構造の推定
局所的に性質の異なる媒質が設定された対象に対して、外部から粒子を注入し、周囲に置かれた観測器でデータを取得します。
そのデータから、内部構造(媒質の分布)を推定いたしました。本解析には、all at once 法を用いました。
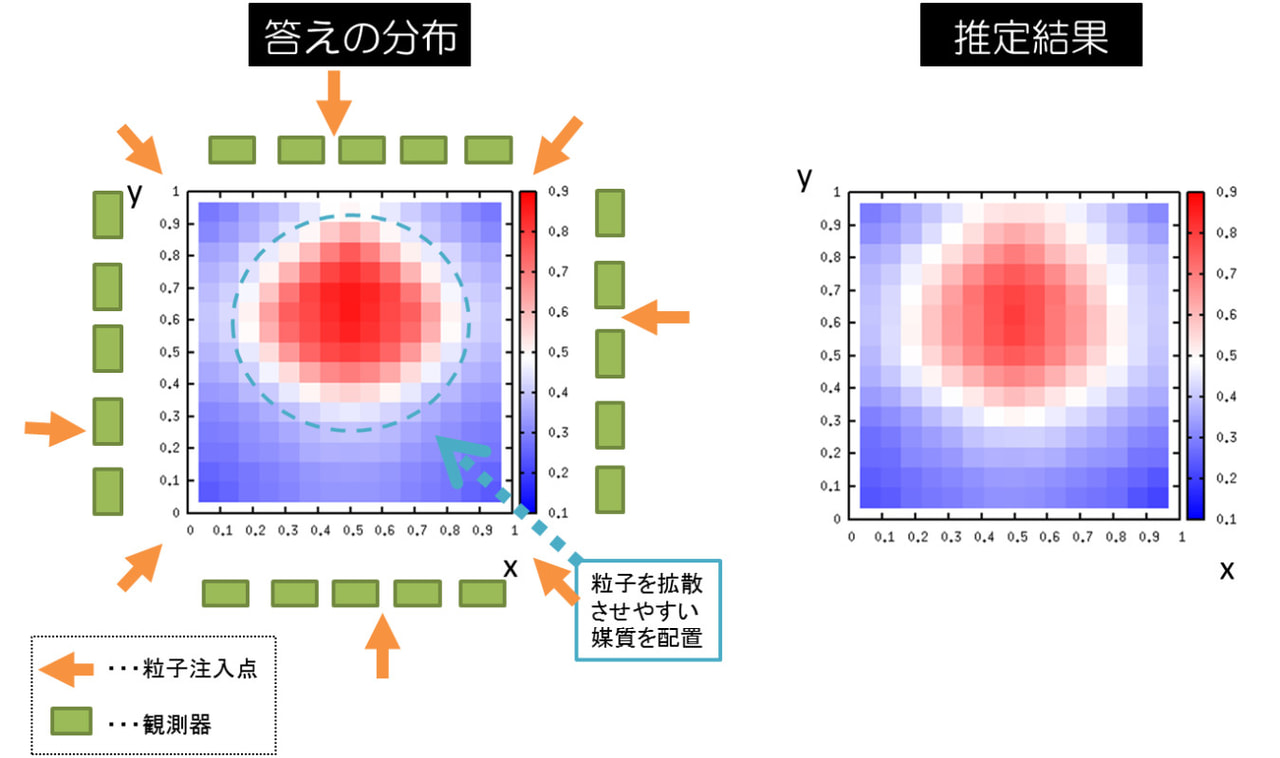
内部構造の推定結果(右)と正解分布(左)の比較
[ black box 法]形状パラメータの自動決定
圧電材料は「電圧」を「機械的な歪み」に、もしくは「機械的な歪み」を「電圧」に変換可能な材料です。
ここでは、前者の性質を用いた振動子を対象として、所望の振動波形になるような形状パラメータを自動決定しました。
細長く加工した Si の上に圧電薄膜(PZT)を積層させ、その上下電極に電圧を加えると、圧電膜に歪みが発生し、厚み方向に撓みます。正弦波電圧を加えると、構造体(片持ち梁)が振動します。
本解析では、振幅1V、周波数1kHzの正弦波電圧を入力した場合、所望の振動波形になるように、Si および圧電膜(PZT)の厚みの値を自動決定いたしました。
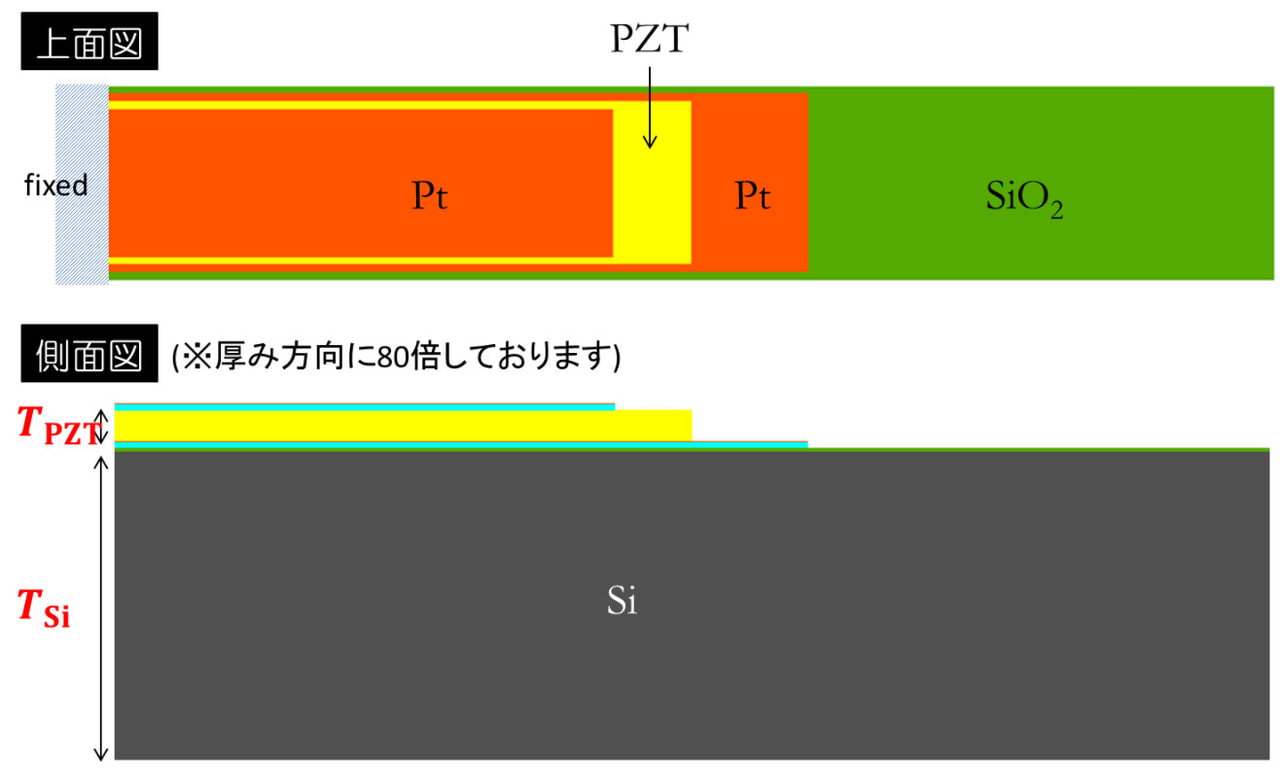
解析モデル(左)と抽出結果(右)の比較
ここでは、black box 法 を用いました。
最適化ソルバとして Nuorium Optimizer を用いた DFO アプローチ、シミュレータとしてマルチドメインシミュレータ MEMSpice を用いました。
両者を繋ぐために、目的関数値の計算プログラムを作成し、「所望の波形」と「シミュレーションで得られた波形」から、差分(ここでは、波形の各点の Euclid距離の平均)を計算するようにしました。
このように最適化部分とシミュレータ部分を独立に用意し、black box 法による逆問題解析が実現できます。
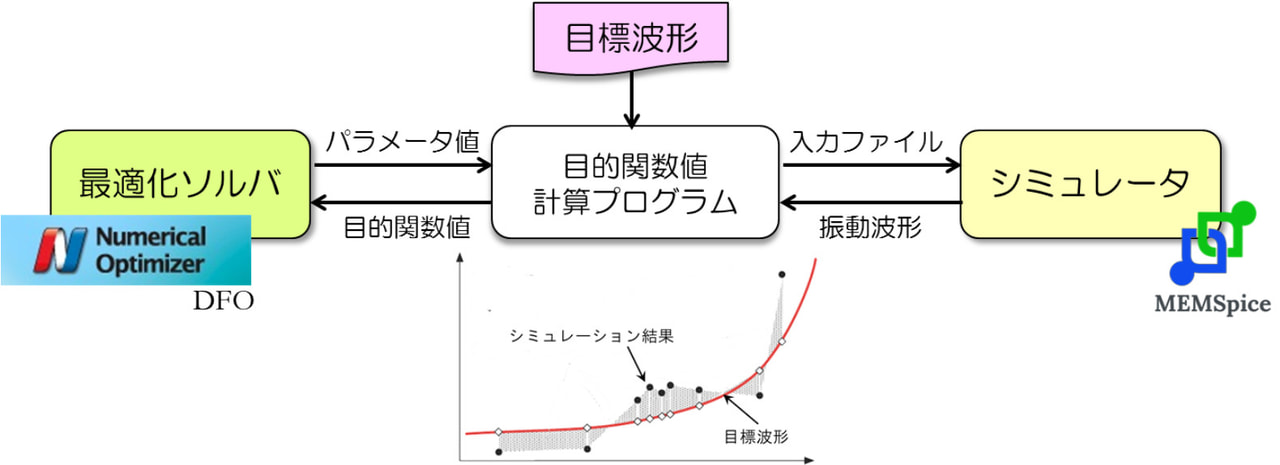
black box 法の実装例
システム化
当社の汎用最適化パッケージ『Nuorium Optimizer』を用いたラピッドプロトタイピングで、システムを構築・課題の洗い出しを行います。それをもとに、扱いたい問題に合わせたシステムを構築いたします。
システム化のフロー
お問い合わせ
株式会社NTTデータ数理システムでは、長年にわたり科学技術計算の業務に携わってきた専門スタッフを数多く擁しており、この経験と知識を皆様の研究開発、設計、製造のために役立てたいと願っております。様々なご相談をお待ちしております。
ご相談はこちら
