数理最適化におけるパラドックス：No-wait Flow-shop Paradox のご紹介

直感と反する結果や受け入れがたい結論が得られる事をパラドックスと言います。 有名なパラドックスとして誕生日のパラドックスやモンティホール問題などがありますが、 数理最適化の分野でもパラドックスが発生します。 本記事では「機械の能力値を改善しても全ての仕事が完了するまでの所要時間が悪化する」という 直感に反した結果が得られる no-wait flow-shop paradox を紹介します。 最初に flow-shop problem とその定式化について紹介し、 その後に flow-shop problem の派生である no-wait flow-shop problem を紹介し、 最後に no-wait flow-shop paradox [1] の具体例を紹介します。

Flow-shop Problem

全てのジョブが同じ工程順序で処理されるような生産スケジューリングを flow-shop スケジューリングと言います。 工程順序が同じという前提から様々な製品を扱うことはできませんが、少品種大量生産に向いた生産方式です。 具体的な問題を見ていきましょう。

次の表にはジョブ J0 から J6 に対して工程 M0 から M3 までの処理時間が与えられています。 J は Job の頭文字です。M は Machine の頭文字です。 工程には一つの機械が対応していると考えて工程と機械を同一視しています。

工程＼仕事	J0	J1	J2	J3	J4	J5	J6
M0	54	83	15	71	77	36	53
M1	79	3	11	99	56	70	99
M2	16	89	49	15	89	45	60
M3	66	58	31	68	78	91	13

全てのジョブは工程 M0, M1, M2, M3 の順に処理されます。 このとき、全てのジョブが完了するまでの所要時間（メイクスパン） を最小化するようなジョブの投入順序及び処理開始時間を求めましょう。

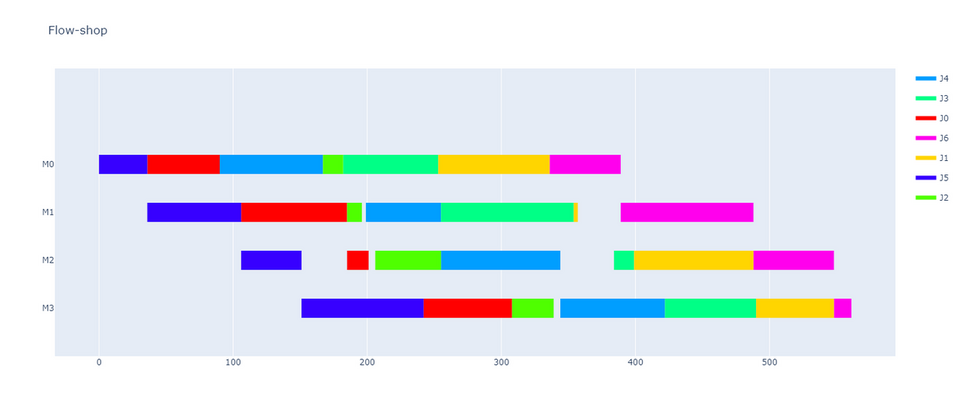
この後に紹介する定式化によって混合整数線形計画問題（MIP）として扱い、最適解を求めた結果が次の図です。 工程 M0 においては隙間なくジョブを処理していることが分かります。 他の工程 M1 や M3 でも隙間がほとんど無く、確かにメイクスパンが最小化された計画であると考えられます。 また、ジョブ J0 が工程 M0 から M1 に移る際に待ち時間が発生していることを確認できます。

Flow-shop Problem の定式化

flow-shop problem には様々な定式化が考えられます。 パラドックスを体験するために最適解が必要となるため、disjunctive model [2] と呼ばれる 混合整数線形計画問題（MIP）の定式化を紹介します。 MIP であれば単体法ベースの分枝限定法によって最適解を得ることができます。 注意点として、flow-shop problem と単体法ベースによる分枝限定法の相性は非常に悪く、 小規模なデータでしか最適解が得られません。中規模以上の flow-shop problem を解く場合は 最適解を諦めて、ヒューリスティクスな解法により解を得るのが一般的です。

(1) は最後に処理されたジョブの完了時間（すなわちメイクスパン）を最小化することを意味します。 (2) は工程 i における処理開始時間は工程 i-1 における処理完了時間よりも後であることを意味します。 (3) はメイクスパンを定義しています。 (4) 及び (5) は工程 i におけるジョブ j と k が disjunctive、つまり交わり無く処理されることを意味します。 (6) と (7) は変数の定義域です。

No-wait Flow-shop Problem とその定式化

先ほどの flow-shop problem の例ではジョブ J0 が工程 M0 から M1 に移る際に待ち時間が発生していました。 このような待ち時間を許さない問題を no-wait flowshop problem と呼びます。 定式化は flow-shop problem において (2) 式を等号にすることで待ち時間無しの解を得ることができます。 先ほどと同じデータで待ち時間無しの計画は次のようになります。

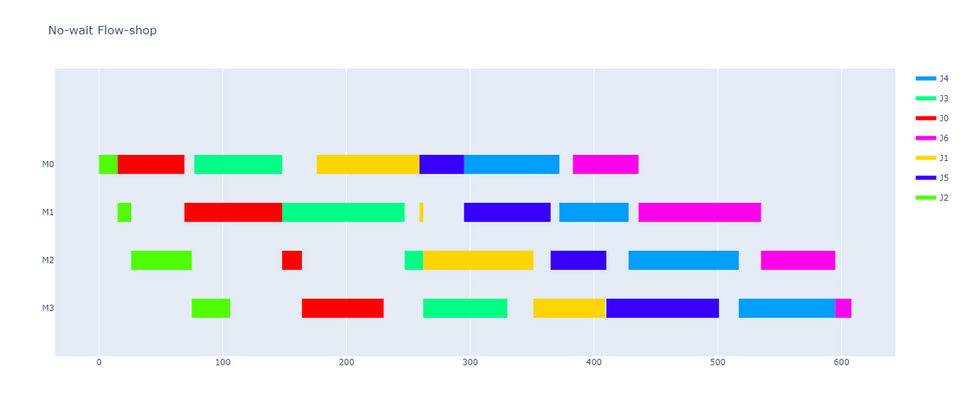
no-wait flow-shop problem の解は flow-shop problem の解です。 一方で flow-shop problem の解は no-wait flow-shop problem の解になるとは限らないため、 no-wait flow-shop problem の方が flow-shop problem よりも目的関数値（メイクスパン）が悪くなります。 「ジョブの待ち時間が無い計画」と聞くだけでとても効率の良い計画のように聞こえますが、 待ち時間を許した方が柔軟な計画が得られるため、メイクスパンが小さくなります。 この時点でやや直感に反した結果が得られている点は面白いです。

PySIMPLE を用いた記述は以下のようになります。

def solve(Jobs, Machines, Times, nowait=False):
    J = Set(value=range(Jobs))     # ジョブの集合
    j = Element(set=J)             # ジョブの添字
    k = Element(set=J)             # ジョブの添字
    M = Set(value=range(Machines)) # 工程（機械）の集合
    i = Element(set=M)             # 工程の添字

    x = Variable(index=(i, j), lb=0) # 工程 i における仕事 j の開始時刻
    Cmax = Variable(lb=0)            # メイクスパン

    problem = Problem()              # flow-shop problem
    problem += Cmax, '(1)'           # 目的関数

    # 処理時間
    p = Parameter(index=(i, j), value=Times)
    i1 = i-1 >= 0
    if nowait:
        problem += x[i1, j] == x[i1-1, j] + p[i1-1, j], '(2)'
    else:
        problem += x[i1, j] >= x[i1-1, j] + p[i1-1, j], '(2)' 

    lasti = Machines-1
    problem += Cmax >= x[lasti,j] + p[lasti,j], '(3)'

    # (4), (5) に必要な添字を定義する
    ijk = Condition((i,j,k), j < k)
    z = BinaryVariable(index=ijk)    # 工程 i においてジョブ j が k よりも先行する
    V = Sum(p[i,j]) # bigM

    problem += x[ijk(0,1)] >= x[ijk(0,2)] + p[ijk(0,2)] - V*z[ijk], '(4)'
    problem += x[ijk(0,2)] >= x[ijk(0,1)] + p[ijk(0,1)] - V*(1-z[ijk]), '(5)'

    problem.solve()

No-wait Flow-shop Paradox 具体例

では文献 [1] で実際に紹介されている具体例を元に no-wait flow-shop paradox を体験しましょう。 次のようにジョブが 3 つ、工程が 3 つの flow-shop problem を考えます。

工程＼仕事	J0	J1	J2
M0	2	2	6
M1	2	6	2
M2	6	2	2

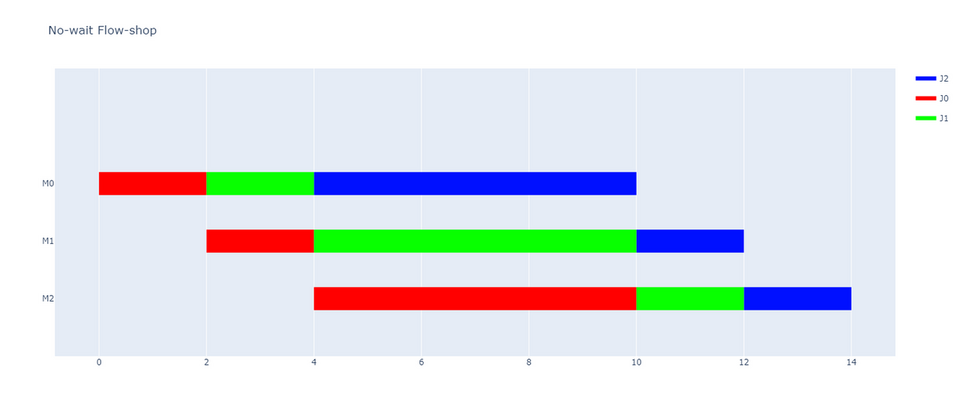
このような入力データの場合、flow-shop problem と no-wait flow-shop problem の最適解が一致し、 メイクスパン = 14 となるガントチャートが得られます。

ではここで、工程 M1 で使用している機械の性能を上げて no-wait flow-shop problem を解くとどのような計画が得られるでしょうか。 「機械の性能を上げればメイクスパンが小さくなる」 という直感が皆さんの頭の中にあるはずです。 実際にやってみましょう。工程 M1 に用いている機械の性能を 2 倍に上げて、処理時間を半分にしてみます。

工程＼仕事	J0	J1	J2
M0	2	2	6
M1	1	3	1
M2	6	2	2

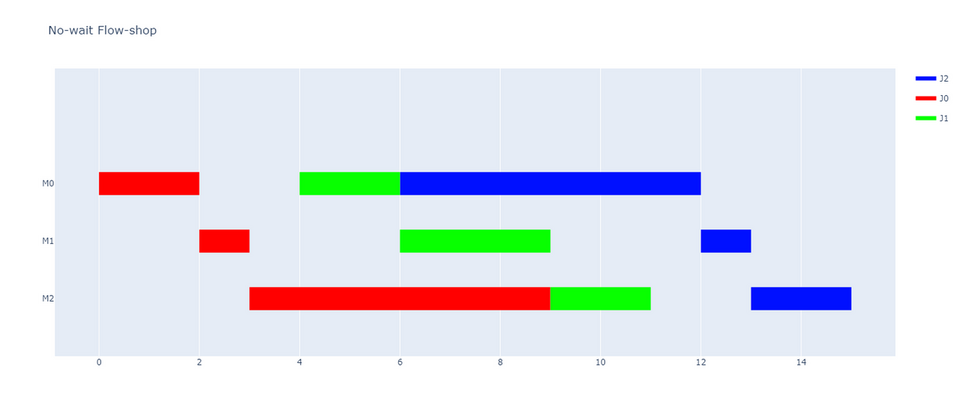
メイクスパン = 15 となる解が得られました。機械の性能を上げているにも関わらずメイクスパンが増えています。

通常の flow-shop problem として解くとメイクスパン = 13 となり、機械の性能を上げるとメイクスパンが減少するという直感通りの結果が得られます。恐らく、no-wait という条件付けがこのようなパラドックスを生む要因だと考えられます。

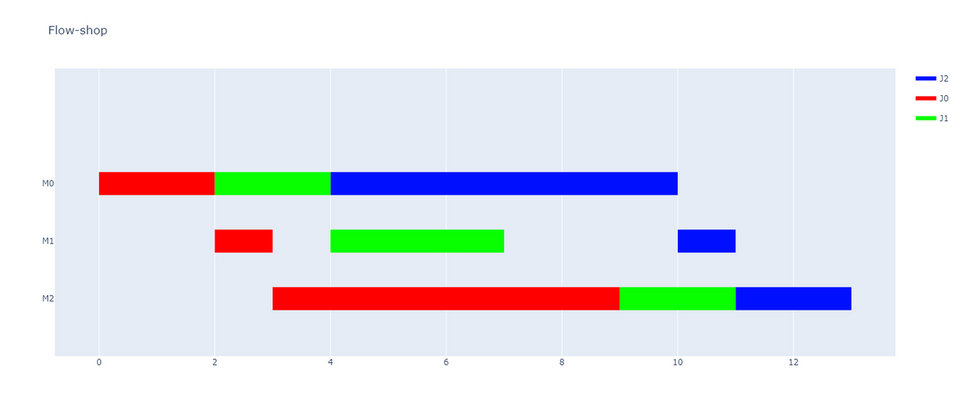
文献 [1] ではいくらでもメイクスパンが悪化するような no-wait flow-shop problem と機械の性能の上げ方が存在することが証明されています。 一方で、パラドックスが発生する条件は解明されていないようです。

終わりに

本記事では数理最適化においてあまり知られていないパラドックスの例を紹介しました。 他には輸送問題でもパラドックスが存在します。そちらではパラドックスが発生する条件も研究されています。 興味のある方は transportation paradox で調べてみてください。

また、今回の例のように直感に基づいた施策をおこなった場合、部分的には改善しているように見えても全体では改善していない（むしろ悪化している）ケースが業務にも存在している可能性があります。 施策を実施する前に一度立ち止まり、数理最適化技術やシミュレーション技術を用いて検証することが大事ですね。

参考文献

[1] Spieksma, Frits CR, and Gerhard J. Woeginger. "The no-wait flow-shop paradox." Operations Research Letters 33.6 (2005): 603-608.

[2] Ku, Wen-Yang, and J. Christopher Beck. "Mixed integer programming models for job shop scheduling: A computational analysis." Computers & Operations Research 73 (2016): 165-173.