ブラックボックス最適化による偏微分方程式の逆問題解析

ブラックボックス最適化 とは、最適化したい関数の内部構造（式・勾配・解析的な形）がわからない、あるいは取得できない場合に、その関数を直接評価することだけを手がかりに最適解を探す手法の総称です。最適化したい対象は「ブラックボックス」として扱われ、入力を与えると関数値を得ることはできますが、内部でどのような計算が行われているかは不明です。

このため、勾配を使う通常の最適化（勾配法・ニュートン法など）が使えない環境で特に威力を発揮するアルゴリズムです。具体的には、

• シミュレーションベースの最適化（目的関数が数値シミュレーションで記述されている）
• 実験データにノイズを含む場合の最適化
• 微分不可能な目的関数の最適化

などに幅広く応用されています。

ここではシミュレーションベースの最適化の例として、近赤外光トモグラフィ の数学的な定式化とブラックボックス最適化アルゴリズムを用いた解析結果について解説します。近赤外光トモグラフィとは、生体に近赤外光を照射して透過してきた光を観測することで、生体内の断層撮影を行う技術です。MRIのように強い磁場を発生させる必要もなく、X線CTのように放射線の被ばくもないことから、安価かつ非侵襲に断層撮影を行うことができる技術として期待されています。生体内部は様々な種類の組織によって構成されており、その種類によって光学特性が異なります。そこで、生体内部での近赤外光の伝搬を記述する輻射輸送方程式の逆問題を解くことでそれぞれの位置での光学特性値を推定し、その光学特性値から組織の種類を推定する、というのが近赤外光トモグラフィの原理です。

問題設定

生体内で近赤外光は生体内部の組織を構成する物質との衝突により、吸収と散乱の影響を受けます。この吸収と散乱の影響を考慮すると、生体内での光の伝搬は次の輻射輸送方程式によって記述されます。

[[ \begin{align*} \frac{\partial u}{\partial t}(t,x,\xi)+\xi\cdot\nabla_xu(t,&x,\xi)+(\mu_s(x)+\mu_a(x))u(t,x,\xi)\\ &= \mu_s(x)\int p(\xi\cdot\xi')u(t,x,\xi')d\xi' \end{align*} ]] [[ t>0, x\in\Omega, |\xi|=1 ]] ここで、$\Omega$は生体を表す領域で$\xi$は光の速度を表します（光の速さを1に正規化しています）。未知関数$u(t,x,\xi)$は時刻$t$、位置$x$における速度$\xi$の光子の密度であり、各項の意味は次の通りです。

• $\frac{\partial u}{\partial t}(t,x,\xi)+\xi\cdot\nabla_xu(t,x,\xi)$ :
  速度$\xi$で運動する光子の動きに沿った密度変化を表すLagrange微分です。
• $(\mu_s(x)+\mu_a(x))u(t,x,\xi)$ :
  散乱や吸収による減少分です。$\mu_s$は散乱の強さ、$\mu_a$は吸収の強さを表す係数です。
• $\mu_s(x)\int p(\xi\cdot\xi')u(t,x,\xi')d\xi'$ :
  散乱されて向きが変わったことにより速度が$\xi$となった光子の増加分です。$p(\xi\cdot\xi')$は位相関数と呼ばれ、散乱により光子の向きが$\xi'$から$\xi$に変換する確率を表します。

以上のことから、光子の密度の変化は「吸収により消滅したもの」「散乱により向きを変えられたもの」を差し引き、「散乱により別の方向から合流してくるもの」を加えたものとして描写されます。

生体内での光の速度は非常に高速であるため、生体に一定の光を照射し続けた際の定常状態を考察の対象とする場合もあります。その場合、上の時間依存の輻射輸送方程式から時間微分の項を落とした次の微分方程式を考えることになります。

[[ \begin{align*} \xi\cdot\nabla_xu(x,\xi)+(\mu_s(x)&+\mu_a(x))u(x,\xi) \\ &=\mu_s(x)\int p(\xi\cdot\xi')u(x,\xi')d\xi' \end{align*} ]] [[ x\in\Omega, |\xi|=1 ]]

以下では、この定常状態を記述する方程式について考えます。

近赤外光トモグラフィでは、生体に外部から光を照射し、生体内部を通過してきた光を観測することになります。このような境界での照射や観測を考慮するために、以下のように内向き・外向きの境界を定義します。

[[ \begin{align*} \Gamma_- & :=\left\{(x,\xi)\ \middle|\ x\in\partial\Omega, |\xi|=1, n(x)\cdot\xi<0 \right\}\\\ \Gamma_+ & :=\left\{(x,\xi)\ \middle|\ x\in\partial\Omega, |\xi|=1, n(x)\cdot\xi>0 \right\}\\\ \end{align*} ]]

ここで、$n(x)$は$x$における単位外向き法線方向ベクトルです。$\Gamma_-$で照射した光を$\Gamma_+$で観測します。したがって、観測を行うことは次の定常輻射輸送方程式の境界値問題を解くことと等価です。

[[ \begin{align*} \xi\cdot\nabla_xu(&x,\xi)+(\mu_s(x)+\mu_a(x))u(x,\xi)\\ &=\mu_s(x)\int p(\xi\cdot\xi')u(x,\xi')d\xi' \quad x\in\Omega, |\xi|=1 \\ u(x,\xi)&=u_-(x,\xi)\quad (x,\xi)\in\Gamma_- \end{align*} ]] この境界値問題を解くことで、外向きの境界$\Gamma_+$における観測値$u_+(x,\xi)=u(x,\xi) \ (x,\xi)\in\Gamma_+$を得ることができます。このように、内部が既知の生体に光を照射して、観測値を求める問題が輻射輸送方程式の順問題となります。

一方、近赤外光トモグラフィでは、未知の内部構造を持つ生体に光を照射し、その観測値から生体内部の構造を推定しなければなりません。また、その観測も有限回しか行うことはできません。すなわち、入射光と透過光の有限個の組$(u_-^i, u_+^i)\ (i=1, \dots, N)$が与えられたとき、この関係から輻射輸送方程式の未知係数$\mu_s(x), \mu_a(x)$を求めよ、という問題を考えることになります。これを輻射輸送方程式の逆問題といいます。生体を構成する組織は種類によって異なる光学特性値$\mu_s(x), \mu_a(x)$を持つと考えられており、逆問題を解いて求めた$\mu_s(x), \mu_a(x)$を可視化することで近赤外光トモグラフィが実現されます。

ブラックボックス最適化による方法

輻射輸送方程式の境界値問題を数値シミュレーションにより解くことができ、入射光$u_-$と吸収係数$\mu_a$、散乱係数$\mu_s$を与えれば透過光$\hat{u}_+$を求められるとし、これらの関係を

[[ \hat{u}_+=F(u_-; \mu_a, \mu_s) ]]

と書くことにします。このようにして求めた$\hat{u}_+$が観測結果$u_+$に最も近くなるような$\mu_a, \mu_s$が最も良い推定結果を与えるものと考えられます。

そこで、推定結果と観測結果の誤差を最小化する次の最小化問題を考えます。

[[ \underset{\mu_a, \mu_s}{\rm minimize}: \sum_{i=1}^N\left\lVert u_+^i-F(u_-^i; \mu_a, \mu_s)\right\rVert ]]

この問題を解くことにより、シミュレーション結果$ \hat{u}_+ $が観測結果$u_+$に最も近くなる$\mu_a, \mu_s$を求めることができます。

この最適化問題において、$F$を具体的な数式として書き下すことは困難です。このように、数式で書くことができない関数を最適化する手法を ブラックボックス最適化 といい、ベイズ最適化 や CMA-ES などのアルゴリズムが知られています。ここでは、輻射輸送方程式の逆問題にCMA-ESを適用した例を紹介します。

CMA-ESによる計算結果

CMA-ES（共分散行列適応進化戦略）は進化戦略の一つです。解候補をサンプリングする多変量正規分布の共分散行列を適応的に更新するアルゴリズムで、ノイズを含む関数に強く、ベイズ最適化と比較して大規模な問題でも解けるという特徴があります。

今回は、位相関数$p(\xi\cdot\xi')$にはHenyey-Greenstein核 [[ p(\xi\cdot\xi'):=\frac{1}{4\pi}\frac{1-g^2}{1-2g\xi\cdot\xi'+g^2} ]] を用い、$g=0.9$としました。また、簡単のため吸収係数$\mu_a$は既知として散乱係数$\mu_s$の推定を行いました。

以下の図は CMA-ES により散乱係数を推定した結果です。

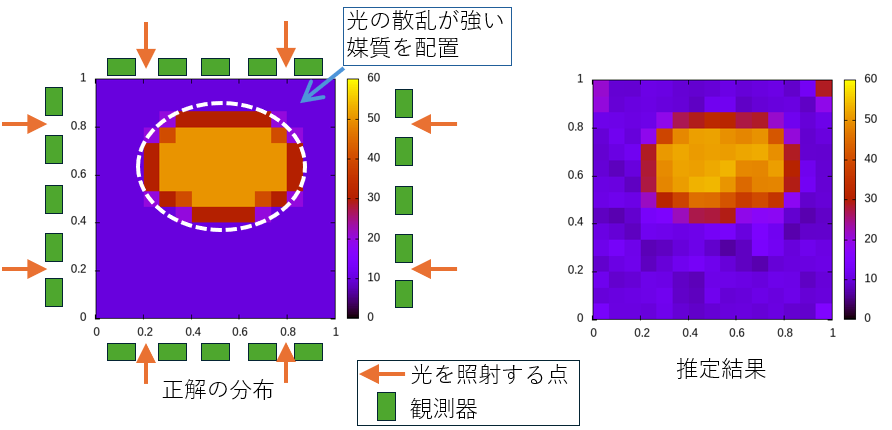
推定された$\mu_s$の値にはややずれはあるものの、散乱が強い媒質が配置された位置についてはほぼ正確に推定できていることがわかります。

終わりに

今回、ブラックボックス最適化の輻射輸送方程式の逆問題への応用事例を紹介しました。ブラックボックス最適化では観測データとモデルの狭間に潜む未知のパラメータや構造を、勾配情報を用いないで推定できるという利点があります。これにより、従来の最適化アルゴリズムでは困難であった領域にも新たなアプローチを提供することができます。

数値シミュレーションの結果を最適化するパラメータ推定は多くの企業の皆様が必要とされているのではないでしょうか。 もしご興味がありましたら株式会社NTTデータ数理システムにお問い合わせください。