講演会を実施しました
NTTデータ数理システムでアルゴリズムの探究をしている大槻です。
先日(2020年10月29日)、拙著『問題解決力を鍛える!アルゴリズムとデータ構造』の出版を記念した講演会を実施しました。おかげさまで、会場と Webinar とを合わせて150名ほどの方にお越しいただきました。
講演に用いた資料は slideshare にアップロードしています。
書籍(Amazonへ)
大槻兼資著、秋葉拓哉監修:問題解決力を鍛える!アルゴリズムとデータ構造 - amazon
講演会の案内と書籍のコンセプト(前回記事へ)
『問題解決力を鍛える!アルゴリズムとデータ構造』出版記念講演会
講演内容
講演会では、主に次の内容について、実体験なども含めてお話しました。
- アルゴリズムの設計技法の紹介
- アルゴリズムの速度性能向上に関する話
アルゴリズムの設計技法
まず、アルゴリズムとは「問題を解くための方法、手順」のことです。アルゴリズムは、実際の問題の解決に活かしてナンボといえます。しかし、実際の問題を解決するアルゴリズムを設計するためには、コツを掴むことが必要です。
そこで書籍では、アルゴリズムを設計するための方法論「設計技法」を重視した構成としました(下図)。書籍の序盤で設計技法を集中的に取り扱っています。そして書籍の後半では、さまざまな典型的アルゴリズムの解説を行なっていますが、設計技法がどのように使われているのかがよくわかるように解説しました。
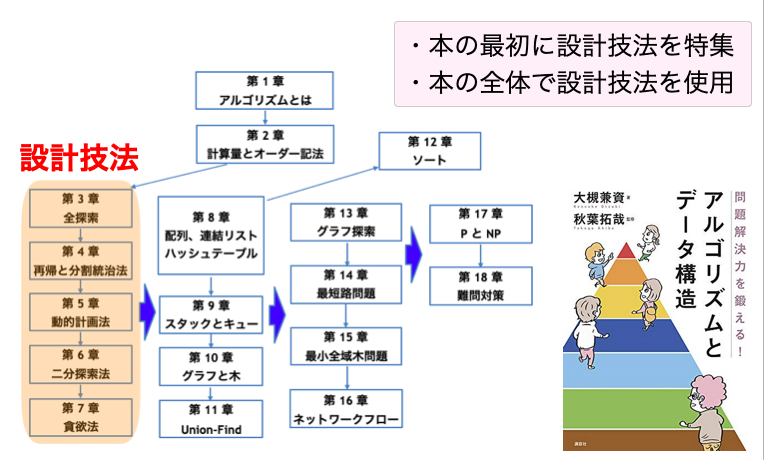 スライド p.9 より
スライド p.9 より
講演では以上の点を踏まえ、さまざまな設計技法を紹介しました。その際には、私が実際に取り組んできた問題に関する話なども含めました。アルゴリズムによる問題解決の臨場感もお伝えできたならば幸いです。
アルゴリズムの速度性能
一般に、同じ問題に取り組んでいても、それを解決するアルゴリズムはいくつも考えられます。そこでアルゴリズムの良し悪しを測るための指標が必要となります。そのような指標として「計算量」が代表的です。計算量とは、問題のサイズに応じてアルゴリズムの計算速度がどのように変化していくかを測るものです。解きたい問題のサイズを $N$ としたとき、次のようになります。
- $O(N)$ の計算量をもつアルゴリズムは、10倍のサイズの問題を解くのに 10倍の時間がかかります。
- $O(N^2)$ の計算量をもつアルゴリズムは、10倍のサイズの問題を解くのに 100倍の時間がかかります。
小さいサイズの問題では、$O(N$) のアルゴリズムも $O(N^2)$ のアルゴリズムも大きな違いはないかもしれません。しかし、問題のサイズが大きくなったときには雲泥の差となって現れます。たとえば、私たちが日常で扱うデータベースも、そのサイズが100,000以上となることはよくあります。その場合、$O(N^2)$ のアルゴリズムを用いては、30分以上の計算時間を要することも少なくありません(下図)。
本講演では、$O(N)$ のアルゴリズムと、$O(N^2)$ のアルゴリズムの違いについて、実体験も交えて紹介しました。とくに、Python のライブラリなどを使用するとき、中身を十分に把握せずに用いると想定よりも大幅に遅いプログラムが出来上がってしまうことが少なくありません。計算量を学ぶことで、世の中に溢れるライブラリなどの速度性能向上の勘所をつかんだり、それらをより上手に応用したりすることができるようになります。
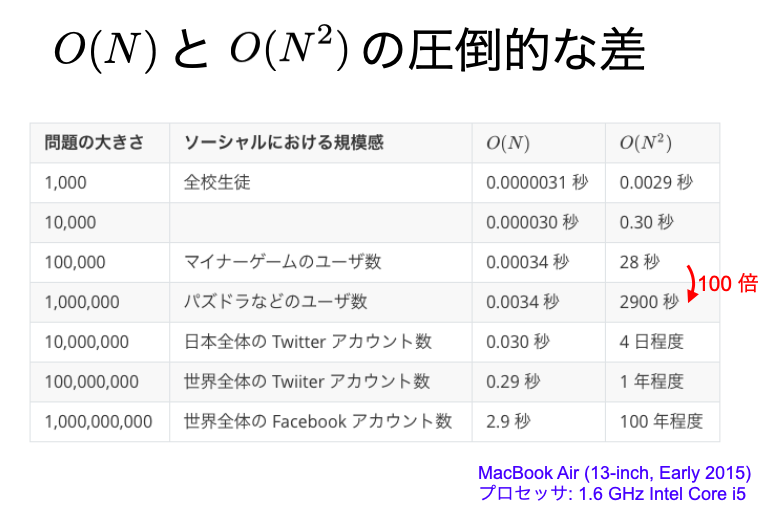 スライド p.89 より
スライド p.89 より
講演会の様子
講演会は開催時間の 15:00〜16:00 のうち、最初の 45 分間を講演に充てて、残りの 15 分を質疑応答に充てました。質疑応答では、
- アルゴリズムの経験を積めば、適切な設計技法が思い浮かぶようになるのか
- どのようにしたら、計算量の見積もりができるようになるのか
- 数独ソルバーを作るときなど、「人間の目の付け所」をアルゴリズムに落とし込むときにはどのような点に注意したらよいか
といった、踏み込んだ内容まで議論することができました。講演会の様子については、後日 YouTube などを通してアップロードさせていただく予定です。
なお、講演会のアンケートでは「動的計画法についても聞きたかった」という意見を多数いただきました。実際に本講演では、時間上の都合から、動的計画法については十分に扱うことができませんでした。そこで現在、講演会の第二弾として、動的計画法を中心に取り上げたものを開催することを検討しております。
おわりに
講演会に参加していただいた皆様のおかげで、大変楽しく有意義な時間を過ごすことができました。改めてありがとうございました。私自身も、アルゴリズムを学ぶ意義について再考するよい機会となりました。
今の時代は、AI や量子コンピューティングが流行となっています。今更アルゴリズムを意義は薄いと感じる方もいらっしゃるかもしれません。しかしアルゴリズム的思考は、分野の流行がどのように移り変わっていったとしても、汎用的に活用できる一生モノのスキルとなります。むしろ現在は、AI を学ぶための強力な下地になるとさえ言えるでしょう。また、インフラ・サービス・金融・物流・製造・公共・ヘルスケアなど、極めて多岐にわたる分野に対して横断的に活用できることも、アルゴリズムの大きな魅力です。
さらに現在は、小学校におけるプログラミング教育必須化や、高等学校における「総合的な学習の時間」が「総合的な探究の時間」へと変遷していく流れを受けて、プログラミング的思考の重要性が広く認識されてきています。アルゴリズムはまさにプログラミング的思考の根幹をなすものです。そして、アルゴリズムは強力なスキルとなるだけでなく、それ自体が純粋に楽しいものです。いつの時代にも通用するアルゴリズム的思考の楽しさを、一人でも多くの方にお伝えできたならば、とても大きな喜びです。
大槻 兼資
株式会社 NTTデータ数理システム 顧問
NTTデータ数理システムに入社し、数理計画部で数理最適化を活用する業務のかたわらで、Qiitaなどでアルゴリズム・競技プログラミングなどの解説記事を執筆し人気を集める。
現在は顧問となり、数理工学・コンピュータ科学のエバンジェリスト活動・執筆活動で活躍。
drken - Qiita