- HOME
- 量子アニーリングを用いた組合せ最適化問題へのアプローチ
この記事では量子力学を用いた計算手法の1つである 量子アニーリング(もしくは断熱量子計算) について紹介します。
量子アニーリングはゲート型の量子計算と異なり、“基本的に” 汎用的な計算能力(ユニバーサリティ)はありません※が、組合せ最適化問題やサンプリングなどいくつかの有用な問題へ適応可能なメタヒューリスティクスです。
組合せ最適化問題は、ビジネスの様々な局面で現れ、NTTデータ数理システムでも多数の案件を扱っています。
参考記事
数理最適化とは?最適化による効果や導入プロセスを紹介
難しくても使いこなす組合せ最適化(1) ー問題例と解き方ー
難しくても使いこなす組合せ最適化(2) ー組合せ問題の「難しさ」とはー
今回は量子アニーリングを用いた組合せ最適化問題へのアプローチと、従来の量子性を用いない古典手法との比較について解説します。
※:後述する拡張によって汎用的な計算能力を持たせられることが知られています。
イジング模型
量子アニーリング(QA)は物理の言葉では イジング模型のエネルギー基底状態を探索する手法 ということになります。
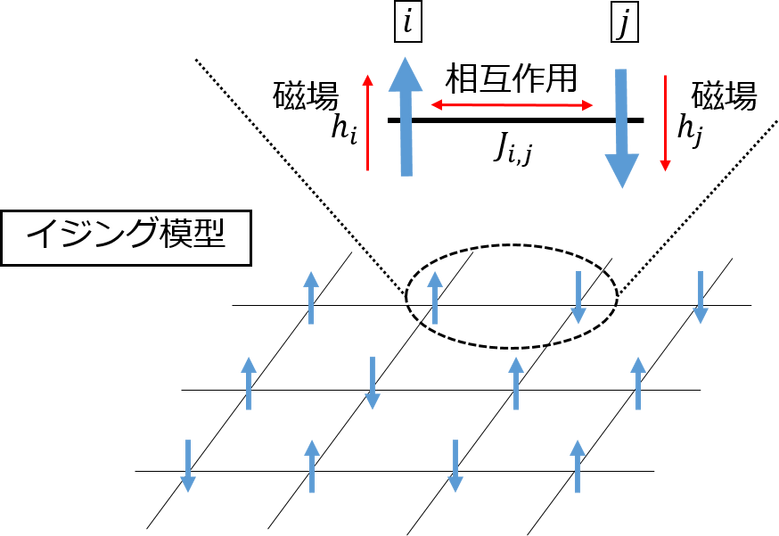
イジング模型 とは物性物理学における磁性体のシンプルな数理モデルです。格子上に並んだ スピン(小さな磁石) 同士が互いに 相互作用 を受けたり、 磁場(バイアス) の影響受けたりしながら各々のスピンが上向き↑下向き↓のどちらを向くべきかを探っています。
イジング模型全体の状態は↑↓↑↓のような各スピンの向きの組合せで定まり、イジング模型ではこれら1つ1つの状態に対して ハミルトニアン(エネルギー関数) が定義されています。そして、エネルギーが最も小さい状態を エネルギー基底状態 といいます。 [[ {\bf イジング模型のハミルトニアン:}H=\sum_{i,j}\underset{{\bf 相互作用}}{J_{i,j}s_is_j}+\sum_i\underset{{\bf 磁場(バイアス)}}{h_is_i} \\ {\bf i番目のスピン:}s_i=\pm1 \ (+1が上向き, -1が下向き) ]]
イジング模型と組合せ最適化の関係
イジング模型のエネルギー基底状態が探索できれば、組合せ最適化問題を解けることが知られています。
具体的には、組合せ最適化問題に対して、以下のような対応関係がとれるように適切にイジング模型の相互作用や磁場の強さを適切に定めます。
| 組合せ最適化問題の要素 | イジング模型への対応のさせ方 |
|---|---|
| 解 | イジング模型の状態(各スピンの上向き・下向きの組合せ)で解を表現する |
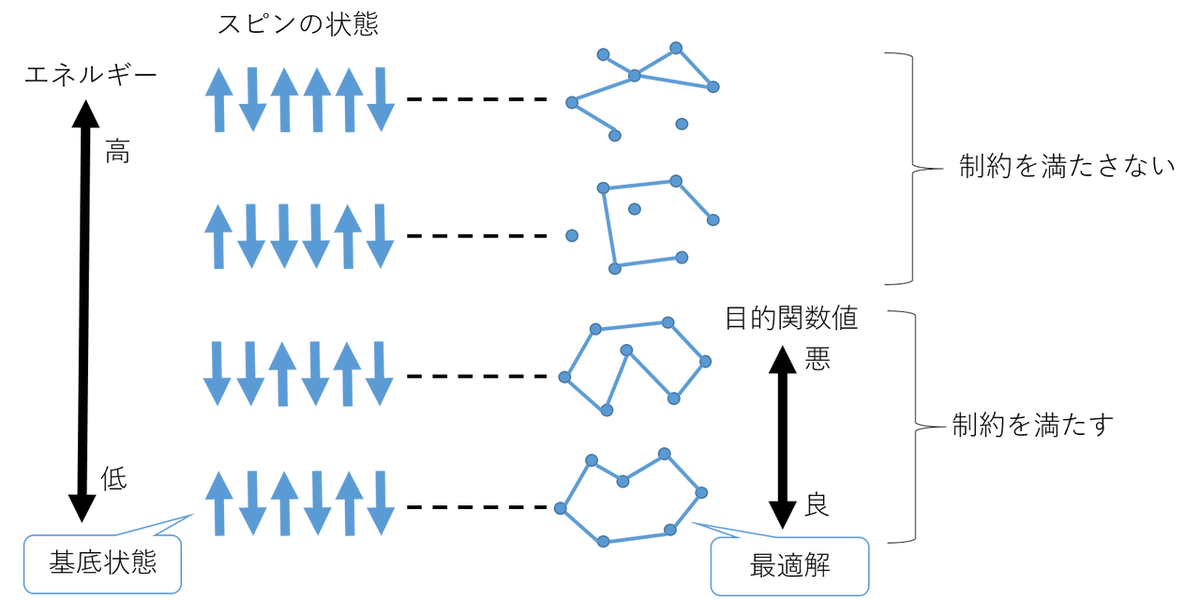
| 目的関数 | エネルギーが低いほど目的関数が良くなるようにする |
| 制約条件 | 制約に違反した解(=スピンの状態)のエネルギーが高くなるようにする |
このように対応づけられれば、イジング模型のエネルギー基底状態を探索することで、組合せ最適化問題の解が得られます。従って、イジング模型の基底状態を高速に探索する手法があれば、組合せ最適化問題を高速に解けることになります。
具体的な問題として例えば、巡回セールスマン問題(TSP)で考えてみます。TSPの場合は、都市を巡回する順番をスピンの向きの組合せで表現します。また、都市間の距離をもとに相互作用や磁場の強さを適切に定めて、巡回経路の長さとエネルギーが比例するようにします。また、制約を満たさない(適切な順回路と対応がつかない)スピンの状態のエネルギーは高くなるようにします。
上は模式図ですが、実際にイジング模型を作成する際は、組合せ最適化問題を一旦 QUBO(Quadratic Unconstrained Binary Optimization) とよばれる 二次形式の制約なし二値変数最適化 問題として定式化することが多いです。QUBOは最適化問題としてみるとイジング模型とほぼ同じ形式であり、相互変換できます。解きたい組合せ最適化問題をQUBOに変換した後、QUBOからイジング模型に変換するという流れです。
量子アニーリング
QAのアルゴリズムはスピンや相互作用といったものを 物理的に 実装した量子デバイス上のイジング模型に対して 量子的な揺らぎ を加え、それを徐々に減らしていきます。そうすること状態を基底状態へと落ち着けるのが狙いです。このように系に対してある種の揺らぎを加えてからそれを徐々に減らす(冷却する)ような操作を、金属加工の手法になぞらえて アニーリング(焼きなまし) と言います。
イジング模型に対して量子揺らぎを加えるにはスピンの上下の向きであるZ方向に対して直交した向き、例えば X方向に磁場をかけること で実現できます。このX方向磁場はイジング模型に元々ある縦磁場と区別するために 横磁場 と呼ばれます。
横磁場をかけただけでは一見するとスピンがX方向に向き揃ってしまうだけのように思えますが、不思議なことにスピンの量子的な性質から、Z軸方向に沿って見たときにはスピンが 上下重ね合わせ状態 となっています。この上下ともとれないような曖昧な状況を指して量子揺らぎを加えている、と表現しています。
こうして加える量子揺らぎですが、QAアルゴリズムの初期段階ではイジング模型のハミルトニアンを無視できてしまうくらい強くかけておきます。 そうすることでスピンは全て強制的にX方向へ向き揃い、Z軸から見ると上下が完全に五分五分で重ね合わさった状態となり、これが横磁場の基底状態となります。 そこから量子揺らぎを徐々に減らして0にしていくのですが、系をまず基底状態にしてからハミルトニアンを 非常にゆっくり時間変化させる と系は基底状態であり続けることが知られています( 断熱定理 )。この時間変化がうまくいくと系の状態は最終的に元のイジング模型の基底状態に辿りつきます。
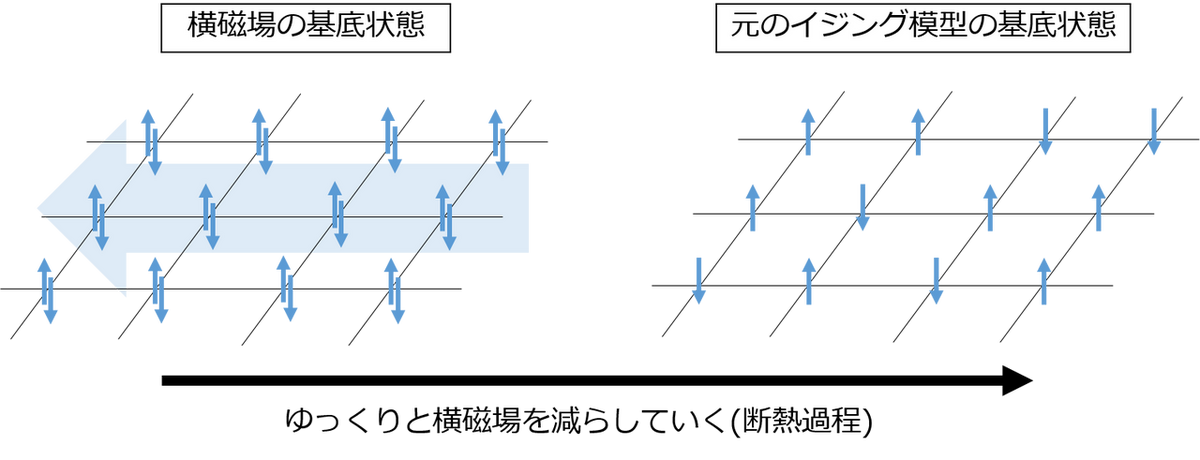
この横磁場の時間変化の スケジューリング はQAの重要な制御パラメータの1つとなっており、解かせる組合せ最適化問題のサイズや構造によって適切なものがあるとされ、それに関する研究が続けられています[1]。またスケジューリングの拡張として、初期状態を重ね合わせ状態でなく適当な局所解とし、そこに量子揺らぎを0から加え、折り返して0へと減らすことで解を改善する(局所解から抜け出す)ことを目的とした リバースアニーリング という手法も提案されています[2]。
古典手法との比較
組合せ最適化問題に対しては古くから様々な手法が考えられてきました。 例えば整数計画問題として定式化できれば、難しくても使いこなす組合せ最適化(2)で紹介したようなアプローチで解くことができますし、他にも様々なメタヒューリスティクスが実際の組合せ最適化問題を解くために使われています。
メタヒューリスティクスの1つとして、熱によるアニーリングを疑似的な乱数に置き換えて数値的にシミュレーションした手法が シミュレーテッドアニーリング(SA) として知られています。SAは量子揺らぎを用いるQAの 古典版 としてよく対比されています。実はQAはSAに対して高速であるという明確な証拠はまだなく、問題に依存して得意不得意が分かれるというのが通説です。QAの量子性の表現としてよく 量子トンネル効果 が挙げられます。一般的に組合せ最適化問題を表現したイジング模型のエネルギーランドスケープは谷(局所解)と山(障壁)が入り混じった複雑な構造を取ります。SAでは探索の過程で、そうした山を登っていくことで向こう側の谷へと行きつくのに対して、QAでは山をトンネルを掘ったかのようにして通り抜けることができます。ただし、これは必ずしもQAに利点があるわけではなく山の幅が広すぎるとトンネル効果はうまくいきませんし、山の高さが低いなら通り抜けるより登り切ってしまう方が効率的な場合があります。実問題のエネルギーランドスケープは急な山と緩やかな山が複雑に入り混じっており、どちらが一方のみが有利な問題というのは人為的に作成しない限りは中々存在しません。
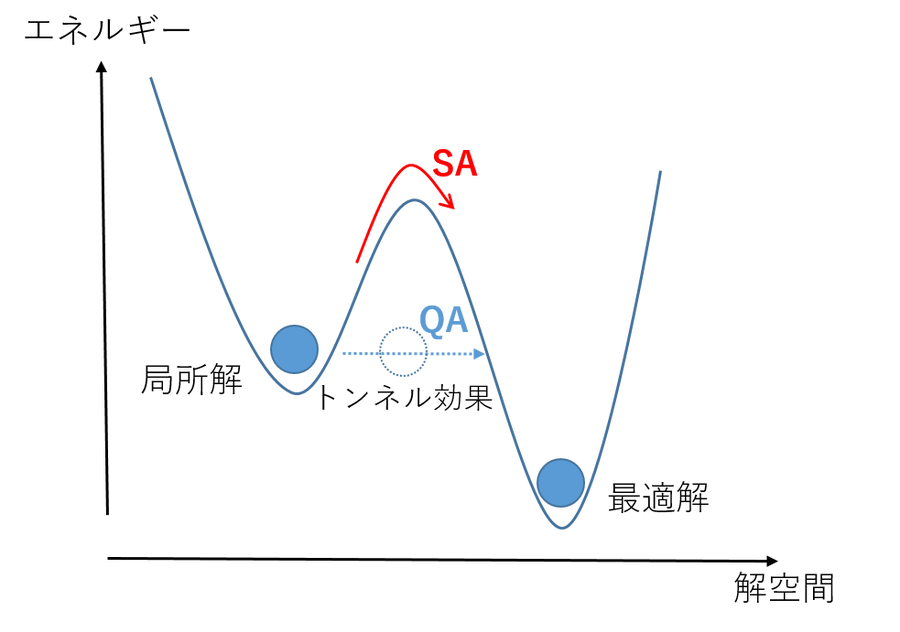
従って、SAを含む何らかの古典手法を用いて問題から部分的な構造を抜き出し、その一部をQAに解かせることで量子の特性を活かし、解精度を向上させる目的の量子-古典ハイブリッドアルゴリズムが活発に研究されています[3]。
もう1つ、 量子モンテカルロ法(QMC) は量子系の時間発展ダイナミクスを古典的にシミュレートする方法で、QAの数値シミュレーションとして、SAとともによく比較に用いられます。QMCの問題サイズに対する計算時間のスケールリングはオーバーヘッドを除いてQAと同等であるとされています。
基本的なQAアルゴリズムはQMCで古典的にシミュレート可能ですが、横磁場の他にXX項(X方向の相互作用)を追加拡張した 非疑似古典(non-stoquastic) ハミルトニアンによるQAはQMCで古典的にシミュレートできないことが知られており( 負符号問題 )、横磁場のみのQAと比べてより強い量子性とそれによる量子加速が期待されています[4]。またこのように拡張したQAにはゲート型量子計算のような汎用的な計算能力(ユニバーサリティ)を持たせることができることが知られています。
おわりに
この記事では、量子アニーリング(QA)を用いた組合せ最適化問題へのアプローチと、従来の量子性を用いない古典手法との比較について紹介しました。
組み合わせ最適化問題をQUBOという形に置き換えることでQAにより最適解を探索することができます。またその探索過程には量子の性質が働き、古典的な手法よりも高速に解が求まる場合があります。メタヒューリスティクスの選択肢の1つとして従来の手法と併用し、量子の長所を生かすことでより高速に解を探索できる期待があります。
QAを実際に実行するには専用の量子デバイスが必要となりますが、この分野ではカナダのベンチャー企業D-Wave Systemsが2011年から超伝導回路を用いたQAマシンの実機を市場に投入しており、日本でも実用化がすでに進められています。
量子性による探索加速の検証や、実問題への適用実験が精力的に進められており、今後その応用事例が増えることが期待されます。
参考文献
- Khezri, Mostafa, et al. "Customized quantum annealing schedules." Physical Review Applied 17.4 (2022): 044005.
- Venturelli, Davide, and Alexei Kondratyev. "Reverse quantum annealing approach to portfolio optimization problems." Quantum Machine Intelligence 1.1-2 (2019): 17-30.
- Chancellor, Nicholas. "Modernizing quantum annealing using local searches." New Journal of Physics 19.2 (2017): 023024.
- Nishimori, Hidetoshi, and Kabuki Takada. "Exponential enhancement of the efficiency of quantum annealing by non-stoquastic hamiltonians." Frontiers in ICT 4 (2017): 2.
http://www.msi.co.jp NTTデータ数理システムができること










