難しくても使いこなす組合せ最適化(1) ー問題例と解き方ー

このコラムは「組合せ最適化問題」という難問、しかし、ビジネスの実務の世界で避けては通れない問題を紹介し、数理最適化という分野の手法でそれを攻略する方法について解説します。まずはこれがどんな感じの問題なのか、習うより慣れろ、簡略化した例題をまずはご覧ください。

組合せ最適化問題の例題

居酒屋ランチ営業バイト募集問題

ある居酒屋でランチ営業を始めることになりました。現場を回すのに必要な人数は大体わかっていて、仕込みの時間では4人、ピークのお昼時には8人は欲しい。時間帯ごとにグラフにすると次のようだとします。

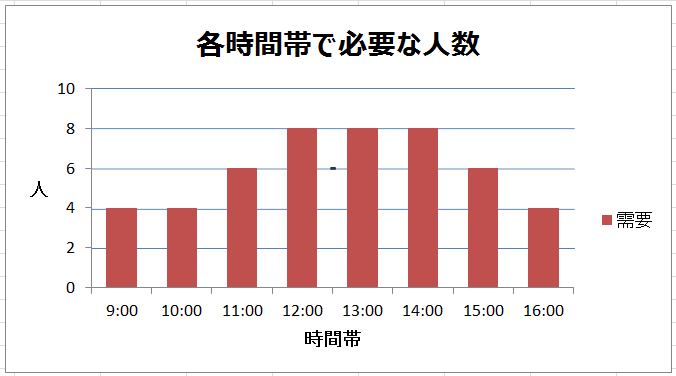
この人数を賄うために、アルバイトを募集するとします。いずれも4時間勤務で9:00スタートから13:00スタートの5パターンのシフトが有り得るとして、それぞれ何人ずつ居てくれたら必要な人数を過不足なく賄えるでしょうか。図の「？」に数字を入れましょう。

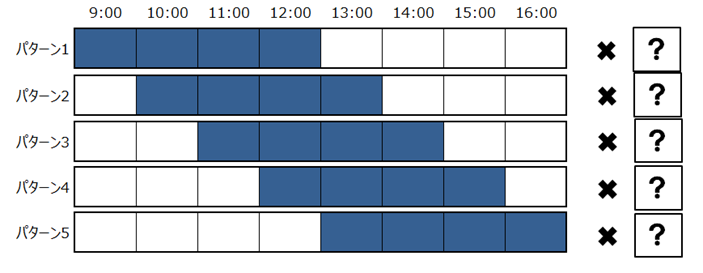
答えは、9:00スタート（一番上）、13:00スタート（一番下）のシフトを4人ずつ、11:00スタート、12:00スタートのシフトを2人ずつ、それぞれ募集すればよいのです。じつは10:00スタートのシフトの募集は不要。

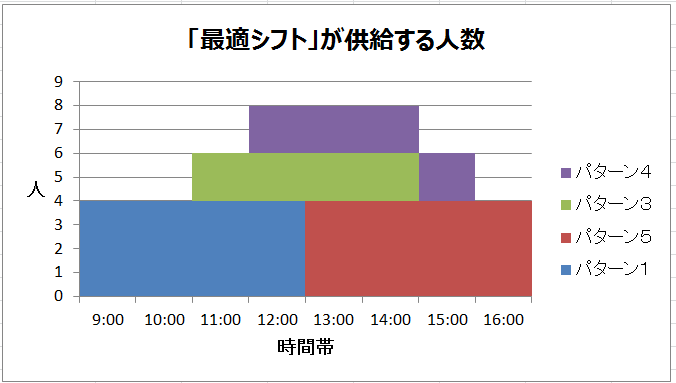
各パターンの人たちがそれぞれ供給する労働力を重ねたグラフを描いてみるとこんな感じ。各時間帯の高さを見ると必要な人数を過不足なく満たしています。これが所望の答えであることは納得せざるを得ないのですが、じゃあ全く白紙の状態から作ってみろと言われてもどうすればよいのかとっかかりが掴みにくい。パターン2が要らないなんて最初からはわからないですね。エクセルにでも向かってとにかく数字をいれてなんとなく調べて答えを出すしかない気がします。

シフトスケジュール問題

これ、なんだかわかるでしょうか。A、B、C、D、E さんの一週間の勤務シフト表です。「日」は日勤、「休」は休暇、「夜」は夜勤、「－」は夜勤の翌日に入る非番を示しています。職場をうまく回すためには日勤は2人以上、夜勤は必ず1人が必要。でも職場の都合だけを優先するわけにもゆかず、みなさん体が辛いので夜勤は一週間で2回以下に抑えることになっています。Eさんは新人なので誰か（この答えではDさん）と一緒に夜勤する、という制約もある。どうでしょう。答えを見せられれば要件を満たせているのはパッと見わかる。エクセルの得意な人なら勤務が足りないところの色が変わるといったシートをあっという間に作ってしまいそうです。ただ、これも全く白紙の状態から出すとなるとやはりあれこれ試行錯誤してみるしかない感じです。

段取り替えコスト最小化問題

4種類の製品を決められた数だけ作ろうとしています。あなたの工場には等しい能力を持つ A から F の6つのラインがあって、どのラインでどの製品を作ることもできる。じゃ適当でよいかというとそうでもなくて、作る製品の「並び」によってはラインの機器の設定を変更したりと結構なコストがかかる、どの程度のコストがかかるかは並びの組み合わせによって違っていて、次のように整理されているとします。

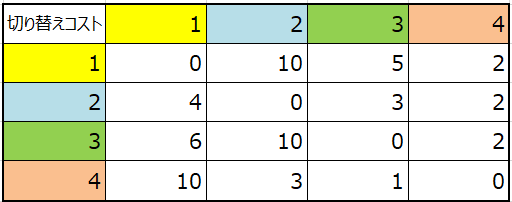
表の記載が親切ではないので、補いましょう。色のついたセルが製品の番号を示していて、表の一番左の列の製品と、一番上の行の製品を並べたときのコストが表の中身の白いセルに書いてあります。表の対角線上に0が並んでいるのは、同じ製品を続けて作れば設定変更などが不要でコストがかからないことを示しています。製品4→製品3を並べたらコストは1だが、製品4→製品1と並べるとコストが10、という具合で、並べ方にはかなり慎重にならねばならないことがわかります。製品を過不足なく作って、製品並びに起因するコストを最小にせよと言われたらどうしますか。

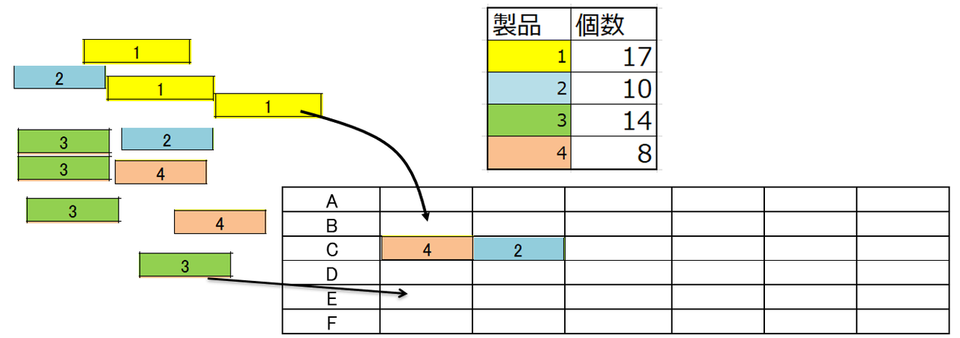
これまでの2つの例に比べてもマス目は多いし、これもどこから手を付けて良いのかわからないですね。でも「1つのラインで一つの製品しか作らない」という方法でコストを最小化する方法はありそうです。例えばこんな風に。

これならばコストゼロです。しかし、どうでしょうかね。一番下のラインFが他と比べてあまりに暇になってしまうのはちょっと受け入れられないかもしれません。例えば各ラインに人が貼りついているのならば各人の稼働の長さにばらつきが出てしまうのは好ましくなく、各ラインの稼働時間（ここでは簡単に製品の割り当て数に等しいとしています）は揃えたいと思うのは自然な要求でしょう。そうすると製品を作る個数がじつに半端な値なので、どこかでコストを支払って違う製品を前後に並べる必要が出てきます。

そろそろ勿体をつけてないで各ラインの稼働を均等化しつつ並びのコストを最小に抑える並べ方の一つを提示しましょう。

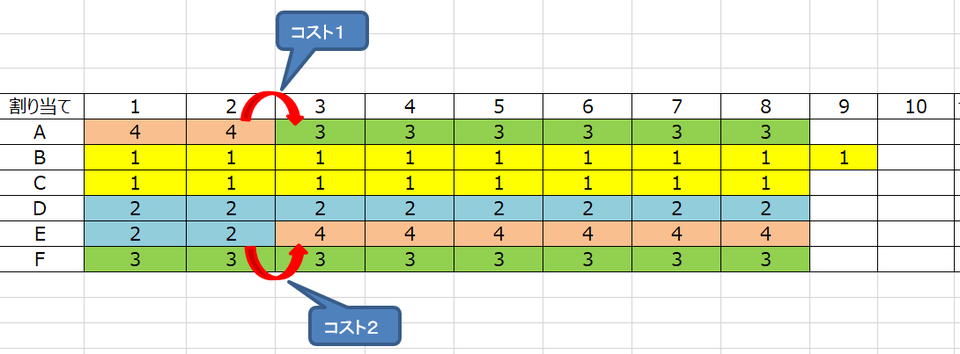
エクセルシート一枚に十分収まる結果でも、見せられると確かに良いのはわかるのですが、いざ作ってみろと言われると手が出ないもどかしさに襲われます。

組合せ最適化問題とは

上に挙げた3例とも、結果は表のセルに適切な数字（0、1、2、3、4）や記号（「日」「休」「夜」「－」）を書き込めば表現できます。すなわちこれらの問題を解くということは、何らかの条件を満たすセルの数字や記号の離散的な組合せを探すことと同じ。このような問題のことを組合せ最適化問題と言います。離散的な組合せを探す、というのは無段階に調整できる「ボリュームスライダー」のようなものを上下に動かすのではなく、ダイヤル式の金庫の鍵のように目盛りのついたところにしか止まらない「デジタル」なつまみを、適切な数字や記号の組合せを求めてカチャカチャ動かす、ということです。この特性を使うと、あり得る答えの組合せの総数を大体計算することができます。

最初の居酒屋のシフトのケースでは、「？」のセルは5つ。入る人数を多めに考えて0人から8人の9通りとすると、すべての組合せは約6万通りになるのでそれなりの膨大さです。一週間のシフト表のケースでは、マス目の数が35、入る記号の種別が4つであることから計算すると、有り得る設定の種類は10の21乗通り。1億を2乗してもまだ足りず、それをさらに10万倍した膨大な通り数になります。ラインへの製品割り当ての問題ではマス目数が60、書き込む製品の種類が何もやらないときを含めて5通り、という大雑把な計算で（左詰めにするという制約を考えるともうすこし小さいですが）シフト表の通り数を2乗しただけの通り数になります。

この「全組合せ数」はセルや書き込む数字の数を増やすとあっという間に膨大な数になる（組合せ爆発、と言います）ので、組合せ問題の難しさを強調するときにはじつに便利な数字であります。「一兆（とかなんとか、とにかく天文学的に大きな数）通り以上の膨大な組合せからアルゴリズムが正解を選び取る」とかいう文言を目にされた方もきっと多いでしょう。

ただ、私の立場から言わせてもらうと、この言い方は全通りをしらみつぶしに調べる（全列挙と言います）という全くもって芸のない探索方法を前提とした一種の「こけおどし」に過ぎません。このような言い方の中には、あり得る組合せの中に良い結果がどの程度の個数含まれているのか（通常「最適解」に限った場合でも実務的な問題設定では答えがかなりの個数あるのが普通で、逆に一つしかない問題設定の方が珍しい、ここは問題を式として表現したり実際に答えを求めたりするのにも重要な着眼だったりするので次回以降で細かく説明します）、あるいは最適解の分布はどうなのか（答えの分布に特徴があるならば効率的な見つけ方を工夫できる余地がある）といった、答えを求める難しさを大きく左右するファクターが欠落しているためです。

そもそもこの手の問題に答えを出してゆかないことには世の中は回りません。この記事を読んでいらっしゃる方にも、これより数段難しい問題をいつも仕事で解いているよ、という方がきっといらっしゃるはず。そんな現場のプロフェッショナルの方々が全列挙を使っているはずはないです。エクセルなどでセルに値を書き込むと組合せの良さを与える補助ツールに向かって、勘と経験であれこれ試行錯誤して、答えを出されているのではないでしょうか。実はこの方法は組合せ最適化の膨大な選択肢に立ち向うための「ヒューリスティクス（heuristics ―　発見的手法という意味）」というアルゴリズムの一つです。人間の経験と勘によるヒューリスティクスはかなり優秀で、何度か似たような問題設定で答えの探索を繰り返していると、「慣れ」てきて、それほど苦労なく比較的満足行く結果の一つや二つ、出すことができます。

でも、普段そうやって出している答えがどの程度良いものなのか、もっと良いものがあるのではないか、考え始めるときりがないのではないでしょうか。今は困ってないにしても埋めるべきマス目の数がもっと増えたら答えを作る労力が増えすぎないかも心配ですよね。その道のプロフェッショナルはこの「どこから手をつけてよいかわからない」問題の解き方を体感で会得されていますが、例えばチームの人数や設備が事業所の合併で倍になった、とかの状況の変化に常に対応できるとは限りません。あくまで「体感」で身に着けたものだからスキル伝承も難しい。

数理最適化という分野は完全ではないながら、こういった困りごとの処方箋となる手法やソフトウエア的道具の追求をテーマとしています。次回以降はもうすこし掘り下げてこの問題が難しい理由や攻略方法のヒント、そして実世界におけるニーズについてお伝えできればと思います。