難しくても使いこなす組合せ最適化(2) ー組合せ問題の「難しさ」とはー

「面倒」と「難しい」の違い

あなたは出勤前の準備をしています。朝食を食べ、ワイシャツにアイロンを掛け、財布を持ち……、やることは多いけど、毎日のことだからそれほど頭を使う必要もない。それぞれの手順にかかる時間も大体「読める」ので、所定の電車に間に合うために、何時に起きればよいかだってわかる。こういうのは「面倒」だけど、「難しい」わけではない。

さて、そこでトラブルが起きます。

いつもの場所に財布がない。

途端にあなたは自動操縦状態を離れて頭を使うことを余儀なくされます。最後に財布使ったのは何時だっけ？昨日の飲み会でお金を払うときだった。それからは定期で帰ったので、財布出してない。ひょっとしてあの店で落としたなんてことは？いやいや、店出てからコンビニで買物したから、財布はそのとき持ってたはずだ。じゃ、家にあるはずだよな。

こうして財布の存在範囲を絞り込んだところで、探索に入ります。ええとスーツのポケットに入れっぱなしだったのか。いやないぞ（探索操作1回目失敗）。ああそうそう上着を着てたんだっけ、あれ、ここにもないぞ（探索操作2回目失敗）。とするとどこだろう、鞄かなあ、おお、いつも使わないポケットに入れてた！（探索操作３回目成功ならびに完了）。……とここまでやっていると、何が起きるでしょう。そう、予定の電車に乗り遅れる。だってたまたま正解につながる探し方を思いつくか、思いついて見つけるまでどれくらいかかるかなんて、あらかじめ読めないですよね。これがどうなるか「読む」のが大変、という「難しい」問題の特徴で、我々が計算機で組合せ最適化を解いているときにまさに経験することなのです。幸い計算機は多少の面倒なら代わりに引き受けてくれて目にも止まらぬ速度で結果を出してくれるので、我々は計算機に解き方の指針を与えて「難しい」問題を「面倒」に変換する技を繰り出すのです。

「読める」、線形計画問題

座標軸を二次元平面にささっと書いて、適当な直線を足します。座標軸も直線の一つだと思って直線で囲われた部分に色付けしましょう。

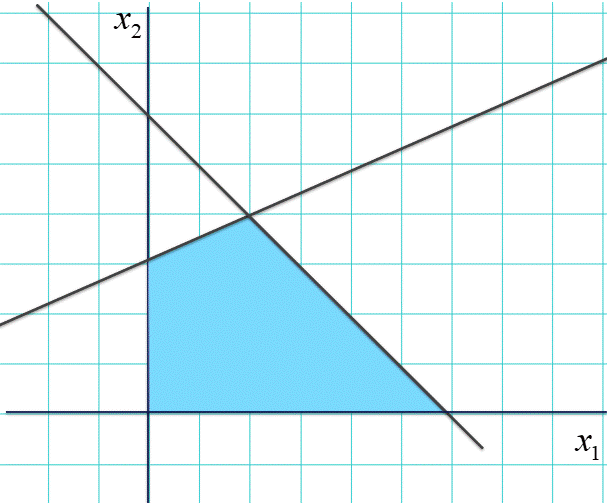
この「池」の中をあなたは好きに動ける。例えば船を漕いで釣りでもしているとしましょう。さて、流れの加減で北の方（絵では上の方）に魚が固まっている、ことを知っているとする。ならば、どこで釣りますか。一番北側の角っこのあたり（下図）ですね。

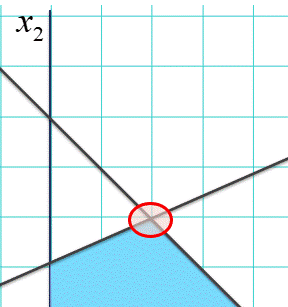
座標で言うと、$(x_1,x_2) = (2,4)$ のあたり。この座標はどうやって出せばよいでしょう。斜めにクロスしている直線二本の交点を求めればよい。この計算（連立方程式を解く）はそれなりに面倒ですが、こういう「面倒」は計算機の大得意ですから、直線の式に現れる数字を入れるだけで、あっという間に交点の座標を求めてくれます。でも、交点の計算はこの問題を解く上で必要だけれど、本質的なものではない。ここで最も重要なのは、「北に行くほど釣れるならば、北にある「角」がよいはずだ」という洞察というか指針、ですね。

この指針はさまざまな状況下で頼りになります。例えば直線が沢山に増えて池に角が増えても大丈夫（下図）。最も釣れそうな場所に赤く印を付けました。

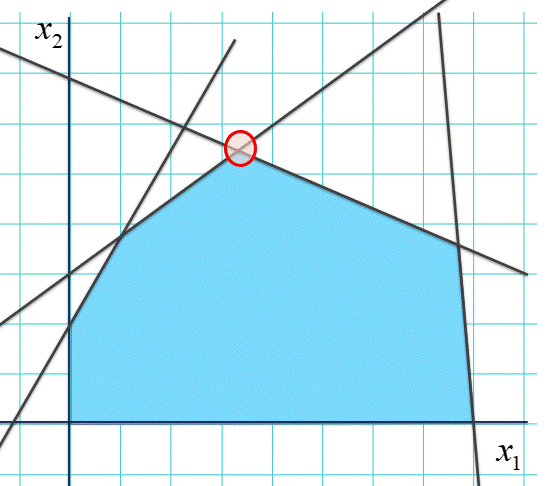
こんなひねくれた形でも大丈夫。

この「指針」はかなり一般的な状況で変わらず有効であることが知られています。具体的には魚のより多く集まる「方角」が分かっていて（とにかく上の方であるほど釣れる）、直線で囲われた形をしている池なら、最良の釣り場は「角」にある（横一線の壁がある池だとその壁一帯すべて最良の釣り場ですが、それでも代表として「角」だけみておけば少なくとも最良の場所を見逃しはしない）。さらに、この場合だと角が少ないのであまり実感はないですが、一般に、ある角を一つ見つけていれば、より魚の居る（少なくとも今より悪くならない）お隣りの角への移動を繰り返すことで最良の釣り場にたどり着けるのです。

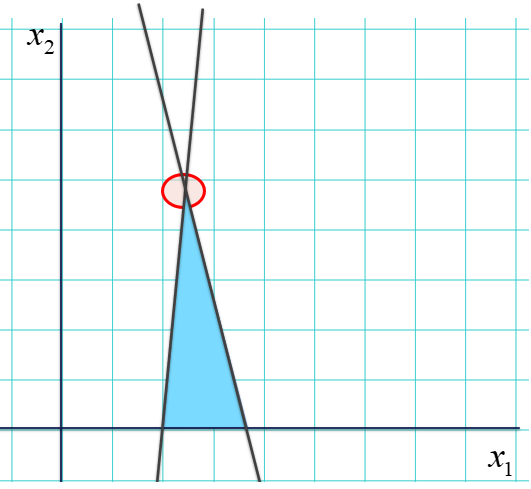
じゃ、もし池がこんな形だったらどうか。

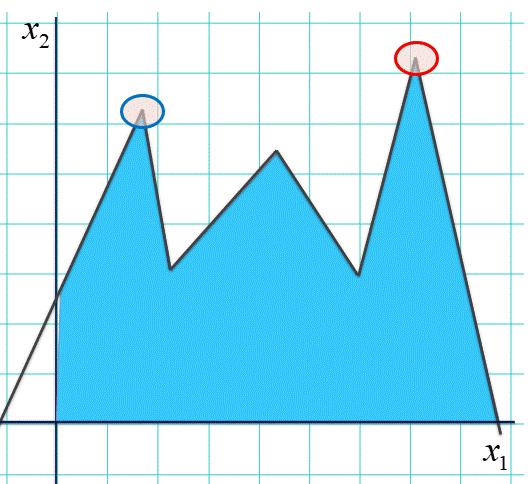
確かにこれだと、青い丸で囲った、そこそこ釣れる左の角を発見しても、釣果が悪くなることを覚悟して一旦南にあるお隣りの角に移る、という勇気を出さねば赤い丸で囲った真の最適な釣り場には到達できません。これは人間でもかなり覚悟が要ることですが、単細胞な計算機には荷が重すぎます。でもご安心を。

ここで前提としているのは池が直線の切れ端である「線分」じゃなくて、どこまでも続く「直線」のみで囲われる領域でしたから、こういう池はそもそ除外できる（池の形は「凸」にしかならない）のです。だから、かならず釣果が悪くならない「お隣りの角」が見つかるし、改善のしようがなくなったら、そこが最適な場所だと断言できる。この理屈は3次元はおろかもっと高い次元でも成り立ちます。

そろそろ種明かしですが、この魚釣り問題は、数理最適化問題の代表的な一つ、「線形計画問題」を絵で描いたものです。線形計画問題は、軍隊への物資の補給方法を決める輸送問題から始まって、石油精製、合金の配合など、産業界において今日に至るまで広く応用されてきました。

この「角（可能基底解）を探せ」という指針は、単体法という線形計画問題の極めて強力な解法の組み立ての基本になっています。産業界での応用では数千個から10万個くらいの変数が現れるのですが、こうなると先程の2次元（2変数）とは違ってもう到底絵には書けない「池」を動きまわることになって、「角」もそれなりに（というか指数的に）多いので何か指針がないととても歯が立ちません。しかし、そんなときにも、どこかの角から始めて、より良い方角に近いお隣りの角を次から次へと手繰ってゆく方法で十分高速に最適な解（「角」）が得られます。 特に計算機とソフトウエアが進歩した最近、例えば5万変数でも1分と待たずに結果が得られるようになった線形計画問題を我々は「難しい」とは認識しません。もちろん、「角」の座標を求めるには、直線（一般次元では平面）の交点を求めるため一次方程式を解かねばならず、様々な「面倒」は起きるのですが、その努力は「読める」範囲になっています。

「読めない」整数制約付き問題

じゃ、「読めない」ってどんなだよ、という話ですね。

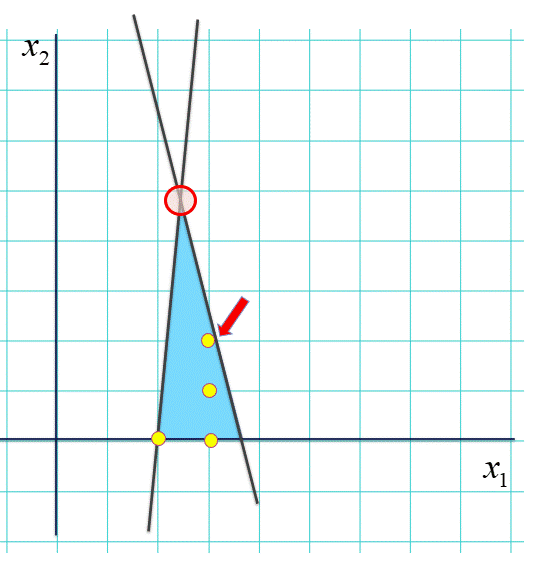
さきほどの魚釣り問題で、船が手漕ぎでどこでも行けるわけじゃなく「自動運転」になったとします。そのために、池の底にビーコンかなんだかが埋まっている場所、うっすら見えていた「マス目」の四隅、すなわち次の図の黄色い点の場所にしか止まれなくなった（答えとして許される座標値に整数制約が付いた）としましょう。すなわち我々は池の中で最も北にある「黄色い点」を求めねばならなくなったとします。最初に使った池の形だとこの図のような感じです。

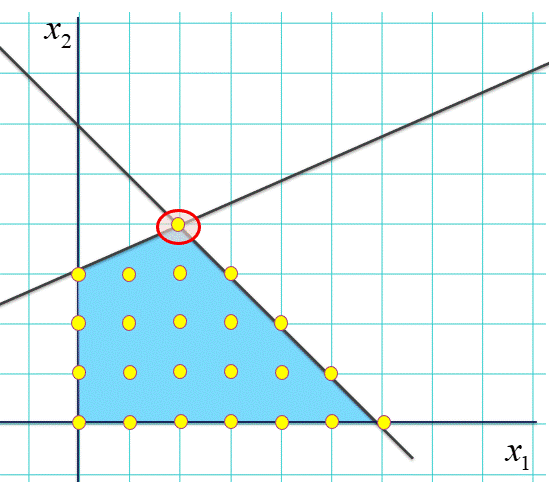
池の形がこれならば、たまたま「角」が黄色の点に一致しているので、手漕ぎの場合の指針に従って最も北にある「角」を辿って探せば、最も北にある黄色の点（すなわち「角」）が自動的に求まる。これは私を含めた津々浦々の数理最適化の実務化が夢見る、「角」を辿って線形計画問題を解くだけで整数制約付きの問題が解けてしまう例の一つ（制約式を定義する行列が特殊な性質（"total unimodularity"）を持つ場合にはこうなることが知られてますので我々は問題の定式化を工夫してなんとかこの状況にならないか工夫したりします）。

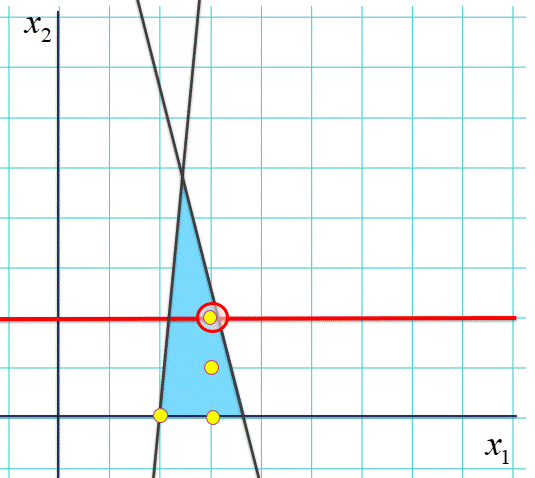
ただ、ご推察の通り、こんなに都合の良いことはいつも起きるわけではない。さきの二つめで使った、線の多いケースだとこんな感じ。

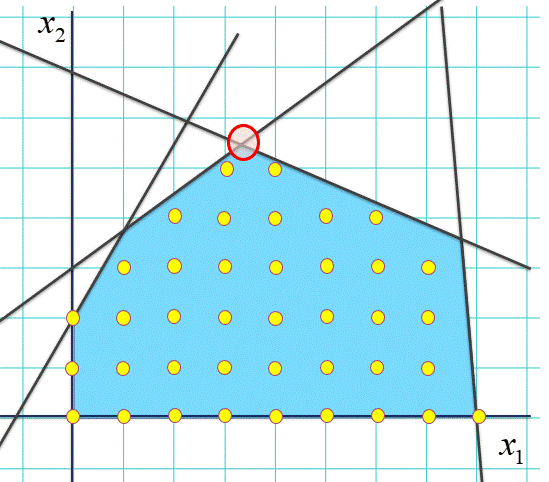
赤いところが「手漕ぎ」の場合の最適な場所でしたが、周囲を拡大してみましょう。

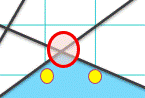
そうなのです。池の「角」は必ずしも船の止まれる黄色の点とは一致しないので、答えになりません。「角」だけ辿っていれば最適解が見つかる先程の状況と打って変わって「読める」とか言って澄まして居られなくなりました。

冒頭の財布探しの話で言えば、居酒屋を出てコンビニで買物するときに定期にチャージしてあったお金を使ってしまったことに気づいて、財布が必ずしも家にない可能性に思いあたったくらいのインパクトと言えましょう。

ま、こんな場合にはすこしもあわてず、「角」の最寄りの、黄色い点を探せばよい（これは、線形緩和と「丸め」によるヒューリスティクス、と呼ばれています）。そうすれば下の図のように、赤い矢印で示した二つの点のどちらかを答えとして出せばよいことはすぐにわかる。

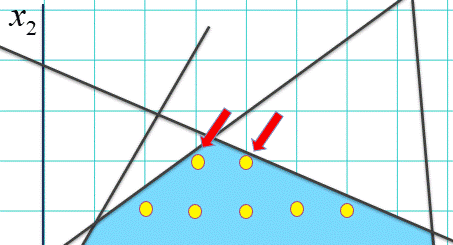
ただ、3つめのひねくれケースだとどうでしょう。

池の形が細長くて、池にある黄色い格子点が少ないため、「角」の最寄りには黄色い点自体が存在しない（「弱い」定式化の整数計画問題）。この場合には、角がどこかなんてあまり気にせず、黄色の点をあれこれ探し回る方法が有利かもしれないですね。

そもそも直線で仕切った領域だけ考えていれば良かったものを、黄色の格子点しか答えにならないとかおかしな制約を導入するからたとえ池の形が同じでもスケールを拡大したり縮小するだけでどこが答えになるか変化してしまう。図形の形とかの性質をうまく使って問題を解くのが数学だよね、こんなの問題の設定自体が不自然じゃないか、とおっしゃる方も居るかもしれません。

ただ、残念ながらこの「自動操縦」ケースの魚釣り、黄色の点でしか止まれない制約（整数制約）付きの問題というのは、現実に避けて通れないくらい沢山現れるのです。

人をどの部署に配属するのか、製品をどのラインで作るのか、限られた枠にどの広告を出すのか、機器のスイッチを入れるのか切るのか、電気を買うのか蓄電池を使うのか……意思決定の問題だと、幾つかの選択肢の中からただ一つだけ選びなさいと迫られる状況が圧倒的に多い。例えば、どの部署でも欲しがるこの人を、三つの部署に "0.3 : 0.2 : 0.5" の比率で割り当てる、とかいう答えでは使えません（実行不可能）。"0 : 1 : 0" （二番目の部署に割り当てる）とか、"1 : 0 : 0" （一番目の部署に割り当てる）とかしか許さない（整数制約）、というのが最適化問題のユーザーサイドの自然な要求として現れます。この要求が、魚釣り問題で言うところの、「黄色の点でしか止まれなくなった」、という状況に相当するのです。

組合せ問題の「難しさ」とは

手漕ぎの魚釣り問題（線形計画問題）は「とにかく池の角を探せばよい」のでしたが、船が自動操縦になって黄色の点でしか止まれなくなったら池の形（問題のデータ）依存でいろんな状況があり得て、効率的に解くには場合に応じてアプローチを工夫する必要がありました。

ああ来たら、こう出るけど、来なかったら、これでしのぐ、とか、解く側に状況次第の臨機応変さを要求するところ、一筋縄でゆかないところが、我々の言う「組合せ問題の難しさ」なのです。決して答えの通り数が何億何兆あるから難しいのではありません（だって池の船が止まれる場所の数は手漕ぎケースの方が無数にありますよね）。

逆に言うと、強面で気難しそうに見える問題も、アプローチ次第であっという間に見通しが良くなって簡単に解ける、という面白さを持つのが組合せ最適化問題で、それが多くの研究者や実務家によって様々な探求が続けられている理由と言えるでしょう。

例えばこの「ひねくれ」ケースですが、自動操縦では行けない（格子点を含まない部分）を切り取る赤い線が、「新たな」池の輪郭として加えられたら、正解の黄色の点のかなり近く、下の図では重なって見えるほどの場所に「角」が現れます。これならば、一旦「角」を見つけておいてその最寄を探す方法が有効になるでしょう。

やりたいことは目で見せられると明らかですが、実際の問題（変数の数が数千とか……）はこんな具合に絵が書けないし、答えを絞り込むのに本当に必要な線を「式」だけ見て割り出さねばならない。というところが難しく、技術開発のし処です。これは我々の最適化ソルバー（Nuorium Optimizer）にも組み込まれ、改良が続けられている切除平面法と呼ばれる技術です。

難しくても向き合う「組合せ最適化」

セールスマンが幾つかの都市をもれなく重複なく回る順路で、経路の総延長が一番短いものを求めなさい、という問題には「巡回セールスマン問題」という名前が付いていて、厳密に解こうとするとどんなに時間があっても足りない、という話を聞いたことがある方もいらっしゃるかもしれません。確かにこれを全列挙（すべての都市の並べ替えをもれなく探索する）という方法で解こうとすると、都市の数が20個でも順路の総数は 100万×100万×100万 くらい、という莫大な数になるので、確かにちょっとしたものです。物流・配送のご相談によく現れる車両巡回問題（ヴィークル・ルーティング）という問題は、この問題をさらに一般化したものに相当します。具体的に言うと「セールスマン（配送車）」が複数になり、「各都市（配送先）」を訪れる時刻に制限（タイムウインドウ）がついて、何かしらのアクション（荷卸しや積み込み）とかもあわせて考え、回る順路を計画する問題ですから一般的に考えればこちらも輪をかけた難問、ということになるでしょう。

でも、だから難しくて解けない、とか、逆にすばらしいソフトウエアや新しいハードウエアが黙っていてもすべて解決してくれるのだ、とかいう言い方は（少なくとも現在のところ）、技術的に誠実な姿勢とは言えません。計算機が多少の「面倒」は引き受けてくれる時代に居る我々ですから、状況次第で臨機応変に工夫する気持があれば付け入る隙はどこかに見つかります。

例えばそれぞれの車が辿る可能性のある経路をあらかじめ列挙しておくとすればどうでしょう。訪問する場所の分布がかたよっていたり、訪問時間の制約がきつかったりすれば、そもそも考慮に値する経路はそれほど多くない。そうして列挙しておいた「出来合い」の経路のどれかを車に「割り当てる」という方法にすれば、この問題はぐっとアタックしやすくなります。もっと細かく言うと巡回経路を求める問題に比べれば、経路の「割り当て」を行うという問題の答えは「角」に近いところにあることが多い（強い定式化の整数計画問題）ので、この性質を有効に使って良い結果を高速に得ることができるのです。

数理計画を生業としている我々の腕の見せどころは、このように組合せ問題の「難しさ」を「面倒」にすることなのです。ぜひご相談ください！ とつい力んで営業口調になってしまうのは、ちょっとした工夫次第で「面倒」にできる問題をただ「難しい」と言って取り組むことなく遠ざけてしまっていることはないかなとちょっと心配しているのです。ここまで強力になった計算機の力や先人の知恵を活用すれば、少なくとも人間が出しているレベルの結果は簡単に、とは言えませんが出せることが普通になってきました。ご相談はどうかお気軽に。

さて、次は架空の魚釣りなんかじゃなく、一つのテーマに基いた組合せ問題を、あれこれ制約を追加しながら数理最適化ソルバーを使って解いてみましょう。そもそもこの手の問題を解いてどんな嬉しさがあるのか、という点にも話を進められればと思います。