難しくても使いこなす組合せ最適化(3) ー数理最適化モデル作りのポイントー

味噌汁メニューとその材料

今回の素材はこの表です。まずはゆっくり眺めてみましょう。

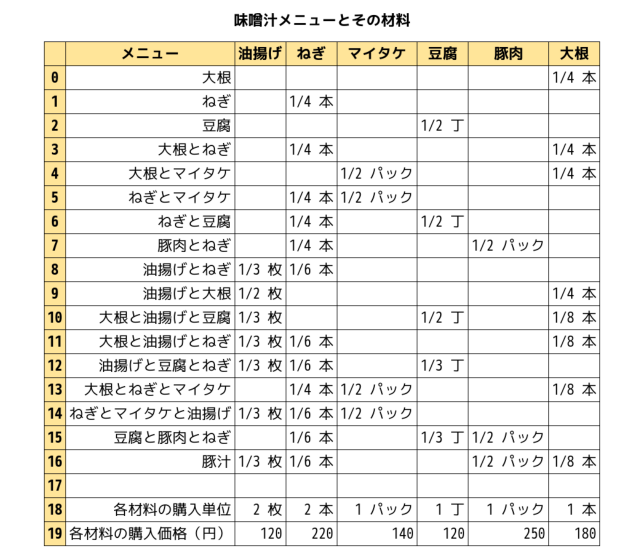
「メニュー」の列に味噌汁メニュー（具の組みあわせ）が17種類（行番号0から行番号16まで）続いていて、各行はメニューに対応しています。右の方の列には、各メニューを作るのに必要な材料の分量が書いてあります。分量の書いてあるところを上に辿ると列の名前から材料の種類もわかるという寸法になっています。

例えば「大根」の味噌汁（行番号0）は大根 1/4 本しか使わない。「豚肉とねぎ」の味噌汁の行（行番号7）を右に見てゆくと、「ねぎ」の列に「1/4本」、「豚肉」の列に「1/2パック」とある。ずっと下の方にある豚汁（行番号16）を見ると、それなりに具沢山な想定です。豚汁にはマイタケを使わないと嫌だ、とかいう議論はまあここでは脇に置いておきます。

分量は3人分くらいを想定していて、使わない材料は空欄のまま。末尾の二行はちょっと毛色が違っていて、材料をスーパーとかで買うとするとどういう単位で売っているのか（購入単位）と、その値段が書かれています。

原因と結果の絡み合いを整理する（組合せ最適化を使う準備）

味噌汁の材料を調達したい、とする。机に向かって買物を計画する..というのはあまりに大袈裟ですかね。この表を大雑把に頭に描いて、スーパーの売場であれこれと考えるのが普通でしょうか。

例えば「油揚げと大根」の味噌汁（行番号9）を作ろうかなとぼんやり考える。じゃ、油揚と大根を買わなくちゃ。でも大根はまるごと1本単位でしか売ってない（最後から2番目の「各材料の購入単位」の行）。この味噌汁だけだと 1/4 本しか使わない（行番号9）から半端だなあ、もうすこし大根を使うメニューを作ろう。同じメニューばかりだと飽きるし、大根を使うメニューはなにがあるかなあ（「大根」の列を縦に見る）、「大根とマイタケ」（行番号4）なら大根も使うし、丁度売ってるのでマイタケも買おう。でもこの味噌汁一回だけだとマイタケも半パック余る。じゃ、「大根とねぎとマイタケ」（行番号13）も作ろう、とかなんとか。

でも、味噌汁の決定は人生の一大事ではないし、悩むのは面倒だし時間もない。何が食べたくなるかなんて今からわからないし、まあ適当に材料を揃えてあとで考えよう。

これが普通の感覚ですよね。しかし、「人生の一大事」でないにしても、もし仕事でこういう種類の決断を迫られたとしたらどうでしょう。判断の根拠をみんなに説明しなければならないし、結果の善し悪しで納期遅れが解消できたり、皆の残業を減らしたりできるとすれば。仕事だから考える時間はたっぷりある。機械（計算機）だって使える。そういうときに頼れる方法、それが組合せ最適化（広くは数理最適化）という手法なのです。

ここで一歩引いて、思考の中身をすこし整理し、機械の力を借りる準備をします。キーワードは「因果関係」。

大根やら油揚げやらの材料を買う、という事象の元を作っている（原因になっている）のは何でしょう。そう、味噌汁メニューとして何を採用するか、という決定です。いやいや、「安売りにつられて大根を大量に買ってしまった」という事象が原因となって「余すのは嫌なので大根を使うメニューを作りまくる」という結果を招くこともあるから逆でしょうか。

いずれにせよ「メニューの選択」と「材料の購入」という二つの事象が絡みあっていて、同時に考えなくてはならない。実はこの「事象の絡み合い」そのものが、我々をして表を縦横に行き来して悩ませる元になっています。数理最適化モデル（数理モデルの1つのカテゴリ）という格好で我々がやりたいことを表現して、我々の意図を機械に伝え、選択肢を探すという作業を手伝ってもらいましょう。

数理最適化モデル作りで一番大切なこと（「変数」を決める原則）

いきなりですが、問題解決を数理最適化に手伝ってもらえるかどうかは、数理最適化モデルを構成する大事な要素である、「変数」というやつが決められるか、ということにかかっています。

「変数」とは、因果関係で絡み合っている事象の中で、「原因」に相当していて、様々な「結果」を招く大元になっているものです。数理最適化とはこの「結果」たちを「いい感じ」に制御するために、「原因」の方をどのように設定すれば良いかを機械に見つけてもらう方法なのです。だから「変数」が大事。まあそれはわかるとして、実際問題として悩むのは「変数」をどうやって探すか、ということです。最適化の教科書とかだといきなり天下り的に与えられたり、「決めたいものを変数と呼べばよい」とか、簡単に片づけられていることが多いので少々細かく説明しましょう。

私なりに定義すると、変数とは「原因と結果が絡みあっている事象のとっかかり」です。味噌汁のケースだと、「メニューの選択」と「材料の購入」が因果関係として絡みあっています。では、このどちらを「原因」として捉えて機械に決めてもらう「変数」とするべきなのでしょうか。

「メニューを選択」した結果として、特定の「材料を購入」が起きるから、「メニューの選択」が「原因」でしょうか。いやいや、「大根を買った」ことに起因して「大根を使う味噌汁メニューを作りまくる」という事象が起きるから、「大根を買う」方が「原因」でしょうか。つきつめて考えるとニワトリと卵ですから、「原因」「結果」という言葉をひねくって考えても結局よくわからない。ここで変数を決めるのに役立つのは次の原則です。

数理最適化の「変数」は事象の「原因」であって、必然的に数値として定まった結果を招くもの、にする。

これに照らすと、この味噌汁材料表が与えられている状況では、「メニューの選択」を「変数」と設定とするのが正解です。理由を具体的に説明しましょう。

この原則のキーワードは「必然的に数値として定まった結果を招く」という部分です。表を見ると、例えばある日のメニューとして「油揚げと大根」（9行目）というメニューを選択したこと（原因）の結果として、油揚げと大根を使うことは、直接の結果として必ず生じてしまうことであって、そこに何ら別の意図は介在しません。「使う分量」という数値がこの表に明確に示されているので「数値として定まった」という要件も満たしています。一方、「材料を購入」は「メニューの選択」の原因と言えなくもないが、 特定の材料を購入したことが、特定のメニューの選択を「必然的に」招くわけではない。例えば「大根を買う」ことはメニューの選択の幅に影響するけれどメニューを実際にどれにするかは、別の意思決定あるいはルールが介在しないと選択できず、「必然的」とは言えないためです。

どんなのを「必然的」と呼ぶかを体感して頂くため、次にいろんなタイプの数理最適化モデルの「変数（原因）」と、そこから「必然的に招く結果」を挙げてみました。

Table 1: 数理最適化モデルにおけるよくある原因（変数）と結果

変数（原因）	必然的に招く結果
製品を作る	原料を所要する、需要を満たす
ある原料を混ぜる	原料在庫が減る、混ぜてできたものの組成が変化する
設備投資して生産ラインを増やす	コストがかかる、生産ラインのキャパシティーが増える
注文に対して在庫を引き当てて配送する	在庫が減る、配送コストがかかる
母材を特定の方法で切る	切り方に応じて所定数の製品ができる、余剰が出る
輸送車両に配送ルートを割り当てる	ルート上の箇所に配達される、運転コストがかかる
ある日、誰かに夜勤を割り当てる	その日の夜勤担当が1増え、その人の週間夜勤可能枠が1減る

右の列に「結果」として並べられているのは、物理現象的な法則、業務ルールや集計計算を介して、必然的に起こっていて、しかも、その影響が定量的に見積られているものばかりです。

数理最適化モデルになるかどうかを見分けるポイント

「必然的に数値として定まった結果を招く」ものを「変数」として選びなさい、というのが「原則」だとちょっと大上段に構えた言い方をしましたが、実はその裏返しとして数理最適化には

必然的に数値として定まった結果を招く「変数」が発見できない対象には、数理最適化は適用できない。

という限界もあります。

例えば、ホテルの部屋とか航空券の価格をうまく設定して売れ行きを増やしたい、という課題があったとします。売れゆき（結果）を生じさせている大元（原因）になっているのは価格の設定に他ならないはずだから、価格の設定を「変数」とし、数理最適化を使って、機械に売れ行きを増やす方法を探させたい、という考え方は自然です。

ただ、一歩下がってこの原則に照らしてみてください。価格の設定がどのように売行きに結びつくかは「必然的に数値として定まっている」でしょうか。大多数の場合、価格設定に対するお客さんの反応がそこまではっきりしていないのではないでしょうか。そうならば数理最適化の出番はまだ先で、まず過去データなど見て、特定の部屋や席を特定の価格で売ったときのお客さんの応答を機械学習などで予測して、上の「味噌汁材料表」のように直接数字として表現できてからですね、ということになります。

組合せ最適化（数理最適化）問題の使い処

「原則」はわかった、でも待てよ、と思われる方もいらっしゃるかもしれません。原因（変数）に対してどんな結果が生じるかがわからない状態ならば、それを知るために機械学習を適用する、というのならまあ理解できる。けれど、変数を決定したことによる結果がわかっている、ましてやはっきり数字で表せているのなら、別に何も機械の手助けなんか要らないじゃないか、と。

確かに、なされるべき決定が一つしかなければその通り。この絵は数理最適化における「変数」のイメージを絵にしたもので、青い部分（「変数」）が取る内容が、青い矢印で示した4つの結果（黄色）を同時に招くことを示しています。

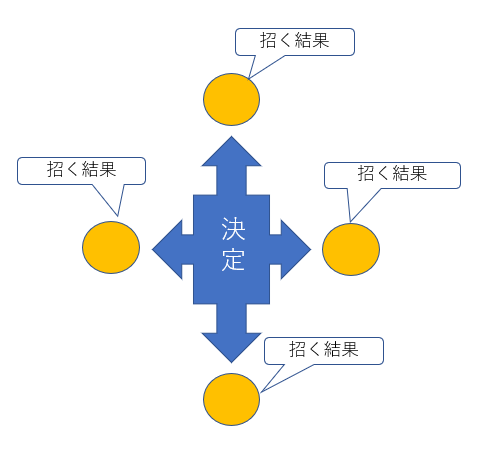
「1つの決定が同時に複数の結果をもたらす」というのはちょっとなじみがない考え方かもしれませんが、例えば製品を所定のロット数だけ作ろうと決めると（変数の決定）、需要を満たすことができる（結果1）一方で、原料在庫を消費し（結果2）、製作に必要な機械を一定時間占有し（結果3）、人手もかかる（結果4）、という風に考えると、変数の決定が招く結果は我々にとって好ましいものもあるし、やむなく起きてしまうけれど、できるだけ制御したいというものもある、ということで複数である方がむしろ自然です。

でもこういう具合に複数の結果をもたらすにしても決定が1個だけ「ごろん」、とある場合ならば、黄色の丸で示されている結果群をそれぞれよーく吟味しながら、人間が決定しても良くて、わざわざ数理最適化を召喚するまでもありません。

数理最適化が重宝されるのは、決定と結果がそれぞれ複数あって互いが競合している場合です。例えば下の絵に示すケース。ここでは「味噌汁メニュー3日分」という3つの決定があります。対応して青いところ（「変数」）がスロットマシンの窓のように3つあって、決定されたあるメニューの並び（「ねぎ」「豆腐とねぎ」「豆腐」）が書き込まれています。青い部分から出る矢印と黄色い丸は、メニューの決定に伴って招く結果、ここでは消費する材料の品目に対応しています。絵の都合で決定から常に4つの矢印が出ていますが、何も書き込んでない黄色い丸に行く矢印は特段注目すべき結果をもたらさないことである、と思ってください。

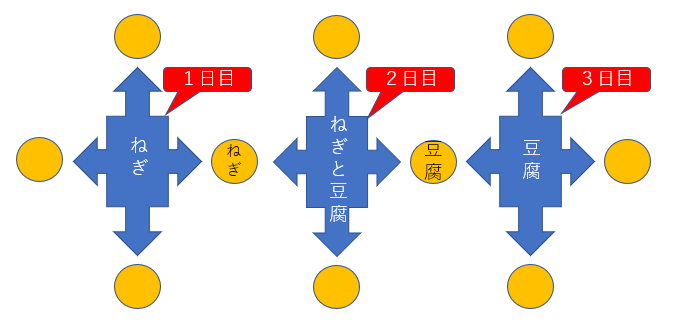
ポイントは、書き込みのある黄色の丸「ねぎ」と「豆腐」に向かっている矢印がそれぞれ複数あるというところ。具体的には「ねぎ」に1日目、2日目のメニューから、「豆腐」に2日目と3日目から、それぞれ矢印が入っていることです。このように2つ以上の決定が同じ結果に繋がるのであれば、一般に各決定は競合関係にあるので独立には決められません。

例えばねぎの在庫が心許なく1/4本しかなかったら、1日目をねぎの味噌汁にすると、2日目の味噌汁は作れなくなるので、この計画は成り立ちません（数理最適化の業界用語で「実行不可能」）。もうすこし複雑なケースだと、ねぎが沢山あったので上のメニューの並びで決まりかかったが、冷蔵庫にある豆腐の賞味期限がぎりぎりになっていることに気づいて2、3日めのメニューを1、2日めにずらそうかと思っていた矢先におとなりから大根を貰ったりすると、大根にひっぱられてこういう風にがらりと変わった並びになることもある。

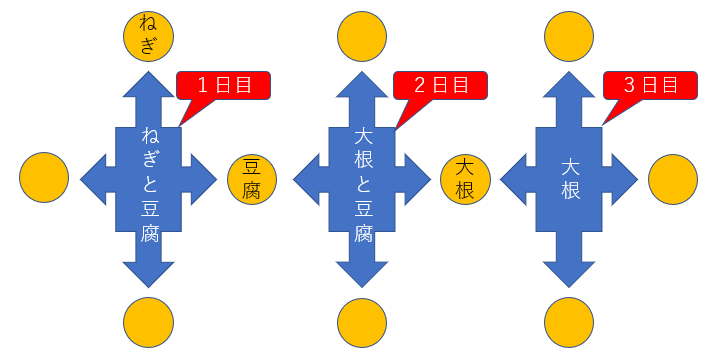
決定同士が互いに依存しているのでこの「がらりと変わる」はかなり自然に起きる話です。書き込む場所が3つしかない状況ならば別にどうということはないけれど、味噌汁メニューも給食みたいに一ヶ月分をまとめて決めろと言われたらどうか。メニューじゃなくて部署のメンバーの各日のスケジュールを決める場合だったらどうか。決定を書き込む場所がびっしり並んでいて、それぞれが招く結果で競合するとしたら。

計画を作っている（青いところに決定を書き込む）側としては、これはかなりしんどい。予定していた材料が入ってこなくなったり、誰かが休みを取りたいとかと言いだして、ちょっと計画を触ると、あれもこれもと変更が変更を呼び、結構かなりの部分を触ってしまうことになる。うまく収まればよいけど、長いこと変更を続けた上、結局つじつまが合わない袋小路に入り込んでしまうかもしれません。

話を一般化すると、複数の決定が存在して、それぞれが複数の結果を生んでいる状況だと次の絵のように「結果」の一部が互いに競合してしまう（この絵の場合、決定1と決定2の結果、決定2と決定3の結果）。逆に競合しないことの方がまれと言えます。

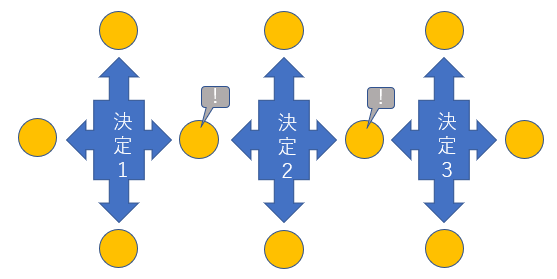
この事情からの自然な帰着として決定1、2、3を独立に決めることはできず、全体の「組合せ」を考慮しなければならない。決定の個数自体はそんなに多くなくても、決定の「組合せ」は結構多い（味噌汁メニュー3日分の場合には (17種類)^3 で大体5千通り、1週間分になると4億通り）。そんなわけで決定の組合せを人手で全部調べつくすのは現実的ではないから、「結果として起こること」が数値化されていることを頼みに、人手にかわってこの決定を行うために召喚されるのが「組合せ最適化（広くは数理最適化）」なのです。

「組合せ」の良さの定義（目的関数と制約式）...は次回のお楽しみ

何を変数にするのか（決定する）のかを決めたら、次はそれぞれの「組合せ」がどの程度望ましいのか、という数値化された「尺度」を機械に伝えるのが次の仕事。それは数理最適化モデルの「目的関数」と「制約式」を決める、という所作を通じて行います。具体的には変数を決定することに伴って生じる、「資源を消費する」「在庫を使う」などの好ましくない結果に対しては「一定以下に抑えてください」と制約する、あるいは「できるだけ小さくしてほしい」という目的関数を設定する。一方「製品が生産される」「お金が入ってくる」といった、歓迎したい結果に対しては、「（需要に見合うよう）一定個数以上作ってください」と制約する、あるいは「できるだけ大きくしてほしい」、という目的関数にする、といった具合です。

目的関数や制約式は「変数」の決定と違って、最初からあまりきっちり考えて設計しておく必要はありません。需要を満たしつつ、設備の無駄な利用を抑えよう、納期はもちろん守らなければ、せっかくだから段取り替えコストを減らしたいし、残業時間も減らしたい、在庫の利用効率や配送のことも考えなくては...、いざ具体的に業務を最適化しようとすると気になることは山程出てきます。ただ、まだ問題を解かないうちから、守らねばならないこと最適化したいことを残らずリストアップして「がんじがらめ」な状態でスタートしようとするのはあまり得策ではありません。

数理最適化が相手にしているのは、変数の決定の結果として複数の事象が同時多発的に発生して双方が絡み合っている現象です。段取り替えコストを減らそうと躍起になっていたら、生産ラインの稼動が均等じゃなくなって作業する人のスケジュールが穴だらけになってしまった。段取り替えコストをある程度折り合わせてラインの稼動を平準化しようと思ったら今度は納期遅れが出たので納期との折り合いも考えねばならなくなった..。という感じで最適化を始めてみると「あちらが立てばこちらが立たず」がそこかしこに発生します。でも、何か一つの事象に着目して良い方向を追求しようとした結果、思わぬところに足が出て、そこを制約で塞ぐ、そうすると別の部分にまた足が出る、という道行きは我々を複雑な現象に対する具体的かつ深い理解に導いてくれる他、現場で計画作成を担当される方々の視野の広さとバランス感覚を再認識、再定義する良い機会にもなります。

数理最適化の環境も進歩して試行錯誤が許されるようになりました。考え込む前にまずはわかる範囲の設定で何か答を出してみて、機械が示してきた結果を見ながら、どういった目的関数と制約が必要なのかを決めてゆきましょう。じつはこれが目の前の現象に対する理解に到達し、良い結果を得るための早道なのかもしれない、というのが我々が最近お客様と業務における最適化を行っていて思うことです。

ちょっと中途半端な気もしますが、今回はここまでにしましょう。「何を決めようとしているのか」（変数）の目星がついていて、その決定が招く「結果」が、「味噌汁材料表」の形できちんと数値として表わせているので、数理最適化を行うスタートラインに立てています。次回からは実際のソフトウェアツールを使って「味噌汁問題」に対していろんな結果を出してみては、制約式と目的関数を調整してまずい部分の穴を塞ぐ、という所作を実際に行ってみます。