数理最適化ソルバの性能評価

ソルバの性能評価

数理最適化の技術は日々進化し、新しいアプローチが提案されています。しかし、これらの技術の「性能」をどのように評価すべきかは、意外と奥が深い問題です。

この記事では、数理最適化愛好家向けに、性能評価の多様性とその背後にある考え方について深掘りします。「価値のある技術とは何か」を読者と共に探求し、数理最適化への新たな知見を提供することを目指します。

求解時間によるソルバの性能評価

ソルバーの性能を評価することは、開発において非常に重要です。そのため、長年にわたって多くの指標が提案されてきました。

初期の段階では、「Performance Profile」と呼ばれる指標が広く用いられてきました。これは複数のソルバに適用可能な方法で、各ソルバの計算時間や反復回数などを比較評価します。各ソルバは、最も良いソルバとの比率で評価がされます。直感的な結果は得られるものの、評価するソルバのグループに依存するなどの問題点も指摘されています。

2000 年代から、「シフト幾何平均（shifted geometric mean）」を用いた評価方法も普及しています。この手法では、ソルバの性能を測定する際に、計算時間に小さなシフト（例えば0.1秒など）を加えた上で、幾何平均を算出します。複数の性能を比較する際は、この数値を比較します。注意点としては、計算時間上限に達している場合、この数値は計算時間上限に依存します。

ソルバの性能評価に関しては、以下の論説もご参考ください。長年混合整数計画問題の並列化を研究されてきた品野勇治博士がコミュニティで推進されてきたベンチマークや性能測定について論じています。

品野勇治. "MIPLIB と Hans Mittelmann’s benchmarks." オペレーションズ・リサーチ 65.1 (2020): 49-56.

求解時間という性能指標を超えて：主積分 （primal integral）

近年、ソルバやアルゴリズムの評価において、単純な計算時間だけでなく、その過程自体の品質を重視する傾向が強まっています。これは、実際のユーザの使い方をより正確に反映した評価を行うことを目指しています。

たとえば、以下の二つの挙動を示すアルゴリズムがあるとします。

• アルゴリズムA: 計算時間が短いが、最適解に到達するまでなかなか良い解を出さない
• アルゴリズムB: 計算時間はやや長いが、初期段階から比較的良質な解を提供し続ける

計算時間だけを基準にするならば、アルゴリズム A が優れていると言えます。しかし、使用状況によっては、初期段階から「良い実行可能解」を提供するアルゴリズム B の方が適している場合もあります。特に、実務での使用においては、完全な最適解を得る前でも、「できるだけ早期に良質な解」を得たいというニーズがあります。

このような問題を解決するために、「主積分 （primal integral）」という手法が提案されています。この手法は、解の品質とその解が得られるまでの時間を総合的に考慮した評価指標です。この指標を用いることで、アルゴリズムが初期段階でどれだけ良質な解を速やかに提供できるか、という観点からも性能を評価することが可能になります。
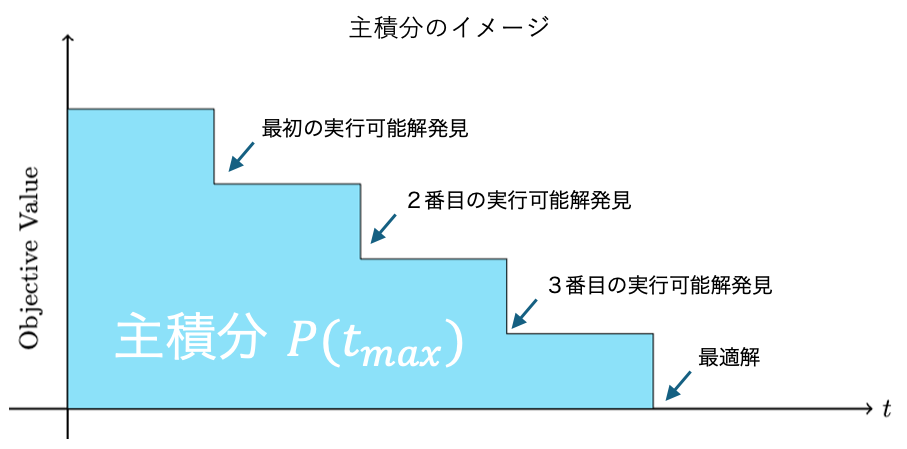
以下は主積分のイメージです。実行可能解の推移を描き、その（正規化した）積分値を評価します。なお実行可能解が求まらなかった場合、主積分の値は計算時間上限と一致します。

参考文献：
Berthold, Timo. "Measuring the impact of primal heuristics." Operations Research Letters 41, no. 6 (2013): 611-614.

機械学習の数理最適化視点での性能評価

ここでは少しはみ出して、機械学習を数理最適化視点で性能評価と関連づけてみます。

機械学習もまた数理最適化問題を解いていると言えます。機械学習、と一口にいっても多くのモデルがありますが （そしてどの範囲を機械学習というかもまた議論が呼ぶ話題でしょう）多くの機械学習は数理最適化問題を解くことによってモデルを得ています。

このような数理最適化視点で機械学習をみた時、「最適解」が常に好まれるわけではないという興味深い現象が観察されます。

たとえば、機械学習モデルのトレーニングにおいては、「早期打ち止め（early stopping）」 という技術がしばしば用いられます。これは、訓練過程でモデルが訓練データに過剰適合してしまうのを防ぐために、ある時点で訓練を意図的に停止する方法です。最適化の人間であれば「せっかくうまくいきそうなのに途中で止めてしまうなんて！」という気持ちになるでしょう。しかしながら、こうした手法によってモデルの汎化性能が向上することがあると言われています。

直感的には、以下のような関数の図で示されます。

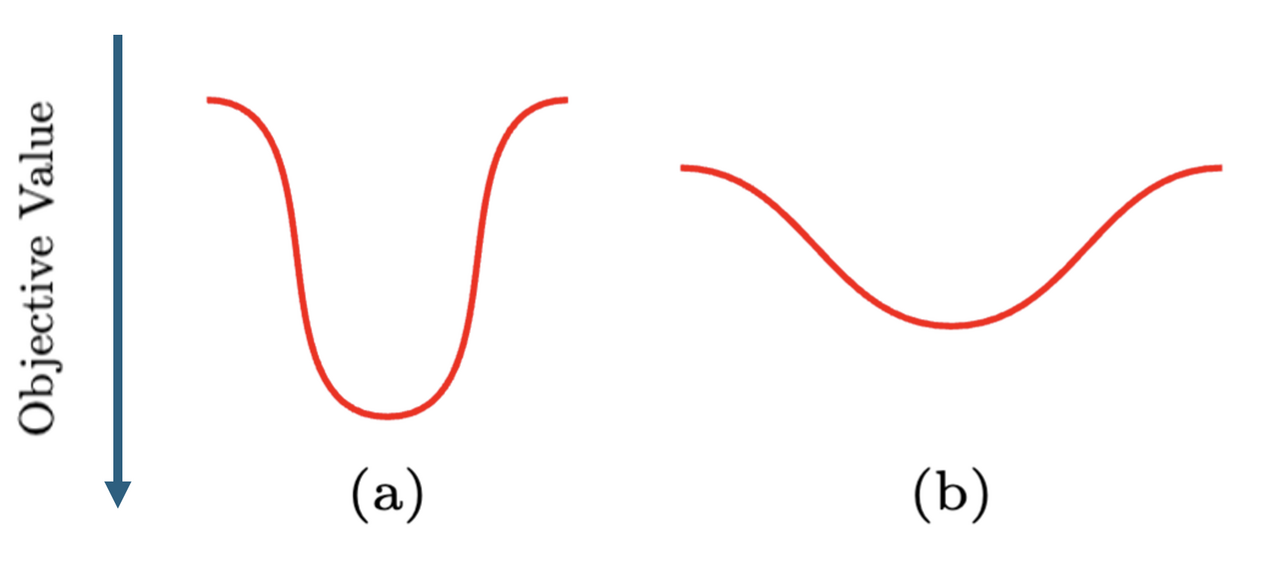最適解の目的関数値は (a) の方がよいですね。しかし見ての通り目的関数の形状は急峻です。目的関数値 (b) の方が、目的関数値は悪いですが、目的関数の形状はなだらかです。非常に大雑把に言うと、early stopping では (a) に行く手前で (b) のような目的関数を取る場所で停止することによって過剰適合を防いでいます。

こう考えてみると、機械学習に限らず、数理最適化の文脈でも (b) のような状況を好むことはありそうですね。数理最適化に与えるデータ自体が誤差を含んでいる場合などはそちらのほうが良いのかもしれません。

今は「最適解」を求めることが主流ですが、将来は広く数理最適化でも「準最適化解（そこそこ良い解）」でなおかつ「頑健な解」を求めたい、というニーズが高まってくるかもしれないですね。

まとめ

今回の議論を通じて、「性能」について多角的に考える機会を持つことができました。一見単純に思える「性能指標」にも、その背後に多様な考え方があることをみてきました。特に、数理最適化においては、単に計算速度を求めるだけではなく、そのプロセスの品質も重要視されることを述べました。

このような視点は、技術の開発や適用において、ユーザのニーズや使い方を深く理解し、反映させることの重要性を示しています。技術は、単に数値上の性能で優れているだけではなく、それを使用するユーザにとって最も価値のあるものである必要があります。このような観点で Nuorium Optimizer の開発を進めていることを本記事を通じてお伝えできていれば幸いです。今後も、ユーザのニーズを第一に考え、数理最適化を通じてより良い未来を創造することが私たちの目標です。