- HOME
- 多変量時系列データ分類「ROCKET」で変数重要度を評価できるようにする
2023年11月21日 19:00
NTTデータ数理システムの数理工学部の大場と申します。本記事では多変量時系列データ分類、およびその手法の一つであるROCKETについて、基本的概念から順を追ってご説明します。さらにROCKETに変数重要度を導入した当社研究についても解説します。本研究によりROCKETは実務でさらに活用しやすくなりました。
多変量時系列データとは？
まずは分析対象のデータについてご説明します。
時系列データとは時間の経過に伴って観測されるデータのことを言います。例えば、1年間の毎日の気温の変動を考えてみてください。1月1日、1月2日、1月3日...という風に日々の気温が記録されていくのが時系列データです。
| 日付 | 1/1 | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/7 | … |
| 気温(℃) | 6.6 | 7.1 | 7.6 | 7.5 | 5.2 | 6.8 | 7.2 | … |
これに対して、多変量時系列データは、時間の経過とともに複数の項目や変数が同時に記録されるデータのことを指します。先の例で言えば、1日の気温だけでなく、湿度や風速も同時に記録されている場合、これは3変量の時系列データとなります。
| 日付 | 1/1 | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/7 | … |
| 気温(℃) | 6.6 | 7.1 | 7.6 | 7.5 | 5.2 | 6.8 | 7.2 | … |
| 湿度(％) | 36 | 43 | 51 | 53 | 47 | 44 | 31 | … |
| 風速(m/s) | 1.9 | 1.2 | 1.4 | 1.8 | 1.3 | 1.8 | 2.1 | … |
多変量時系列データ分類とは？
一般にデータ分類とは、与えられたデータをあらかじめ定められたカテゴリ（分類ラベル）に分けることを指します。例えば、キュウリの仕分け作業で、キュウリ一本一本の画像から「秀・優・良の等級」や、「大・中・小の大きさ」のようなカテゴリに分類するのもその一例（画像による多クラス分類）です。
多変量時系列データ分類では、前述の多変量時系列データ（時間の経過とともに得られる複数の変数を持つデータ）を、そのパターンや特徴に基づいてカテゴリに分けます。例えば、ある運動選手の1分間の心拍数と歩数のデータを使って、その選手が「ジョギングしている」「歩いている」「休憩している」のうちどの活動をしていたのかを判断するのが多変量時系列データ分類です。
この分類を行うことで、多変量の時系列データから有益な情報や知見を引き出し、それらを多くの分野の意思決定や予測に役立てることができます。例えば以下のような形で応用することができます。
医療診断
応用例：心電図（ECG）などのデータを用いて心疾患を識別する
カテゴリ：正常心拍、心房細動、心室細動などの特定の心疾患
産業機械の異常検知
応用例：機械の振動や温度の時系列データから故障やその兆候をとらえる
カテゴリ：正常運転、メンテナンス必要、故障発生
農作物の健康状態
応用例：土壌の湿度や温度、作物の成長の時系列データを分析して、作物の健康状態を監視する
カテゴリ：健康な作物、ストレスを受けている作物、病気の作物
スポーツ選手のコンディションモニタリング
応用例：選手の心拍数、走行距離、スプリント数、血中酸素レベルなどのデータをリアルタイムで収集し、選手のコンディションをモニタリングする
カテゴリ：選手がピークコンディションにある、疲労が蓄積している、怪我のリスクが高い状態にある
ROCKETとは
ROCKETは、先ほどの多変量時系列データ分類のための一手法です。以下のようなステップで分類を行います。
- カーネルの生成:
多数の畳み込みカーネル（特にROCKETカーネルとも呼ばれます）を生成します。これらはCNNで使用される畳み込みカーネルに似ていますが、長さや重みなどのパラメータをランダムに選んだ固定値とする点が特徴的です。 - 特徴量計算:
生成されたカーネルを時系列データに適用して畳み込み、特徴量の元となる量を計算します。具体的にはデータの一部分を切り出して内積を取ることでデータに対する重み付けを行います。さらに畳み込んだ結果に対してプーリング（例えば、最大値だけを残す、あるいは、正の数の比率を計算する）を適用し、最終的な特徴量を抽出します。このプロセスにより、時系列データの特定のパターンの強度や広がりなどが特徴量の形で捉えられます。 - 分類:
最後に、上記のようにしてカーネルの数分だけ得られた多数の特徴量をもとに、データを所定のカテゴリに分ける作業を行います。この部分は、一般的でシンプルな分類器（＝機械学習の分類モデル）を使用できます。
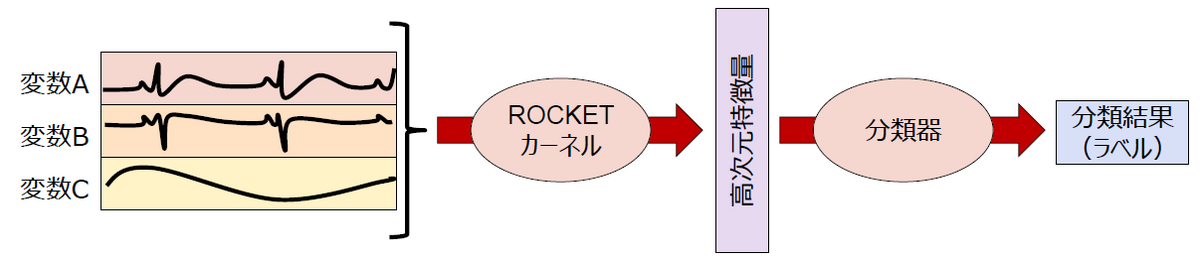
ROCKETでは、「1. カーネルの生成」で述べたように、元の時系列データから一部をランダムに選んで切り出します。そのときの選び方がいい意味で「適当」です。 適当に、ランダムに、とにかくたくさん、数万次元という規模でデータを切り出していきます。「たくさん選べば全体がだいたい見えているだろう」という考え方に基づいています。 さらに、切り出し方だけではなく、重み（ROCKETカーネルの値）もランダムです。つまり、二重にランダムになっています。 何が重要なのかはわからないから、とにかくランダムにたくさんデータを切り取って特徴量を作る。そこには不要なものも入っていますが、正解ラベルと一緒に分類器にインプットすれば、学習の過程で自動的に取捨選択され、より重要なものを考慮して結果が出てきます。
ROCKETの強み
多変量時系列データ分類は、さまざまなアプローチで行われてきました。代表的な手法としては、時系列フォレスト（TSF：Time Series Forest）、Shapelet、 WeaselMuse、HIVE-COTEや深層学習（RNN, LSTM, Transformerなど）ベースの手法などがあります。
しかしROCKETには「適当」だからこそ可能な、他の手法にはない強みがあります。
計算効率
高速に動作します。他の深層学習モデルのような手法で必要になる深いネットワーク構造や微係数（勾配）を用いた複雑な学習プロセスがROCKETでは不要です。これにより、大規模なデータセットでも迅速に処理が可能です。
結果として、GPUなどの高価なリソースを必要とせず、一般的なCPUのみで高い性能を発揮します。
汎用性
多種多様な時系列データセットに対して高い性能を発揮します。これは、ROCKETの設計が特定のデータセットの特性に強く依存しないためです。
シンプルさ
ROCKETの基本構造はシンプルです。他手法にあるような複雑なネットワーク構造の検討や煩雑なパラメータチューニングの手間が少なく、実装や実務への適用が容易になります。
このようにいい意味で「適当」なため、処理がシンプルで軽くなり、データから多くの特徴量を作っているので高い精度も得られやすくなります。さらに様々なタスクに比較的容易に適用でき、高速に動作する点は実務において非常に有用です。
ROCKETの弱点
一方で、ROCKETにも弱点はあります。それは「ランダムな多数の畳み込みカーネルによって特徴量を求める」ことに起因します。
- 周期性が強いデータや非常にノイズの多いデータに対しては、LSTMなどの他の手法のほうが優位なケースがある
- ランダムな要素が強く、パラメータチューニングが難しいため、モデルの挙動を人がコントロールしにくい
- 多数の特徴量を生成するため、オーバーフィッティングのリスクがある
- 不定期計測データに対応できない
- 元の時系列データのうち、どの変数が重視されたのか分からない
1～4は主に分析者にとって課題になるもので、手法を選択する際に考慮する観点です。 一方、5は特に専門外のお客様（業務担当などの方）が分析結果の妥当性を吟味する際に問題になることがあります。
「モデルがどの変数を重視して分類したのか」を端的に数値化したものに変数重要度があります。 たとえば、患者の健康状態が正常か異常かを分類する機械学習モデルを考えます。このモデルの入力として、心拍数の変動、血圧の変動、体温の変動などの時系列データが考えられます。このようなモデルが分類結果を出力するのに、どの時系列データ（心拍数、血圧、体温など）をどれだけ重要視したのかを示す指標が変数重要度です。具体的には、心拍数の変動が分類に大きく影響を与えている場合、心拍数の変動に関連する変数の重要度が高くなります。
従来のROCKETでは、このような変数重要度を求めることができませんでした。 （「3.分類」のプロセスで機械学習モデルから分類結果を出したとき、どの“特徴量”が分類に寄与したかまでは分かりますが、さらに“元の時系列データ”のどこを見て得られた結果なのかはわかりませんでした。）
つまり、分類結果をお客様にお伝えするときに「こういう分類結果になった」ということは言えても、「元のデータのこの部分が重要だった」ということは明瞭に説明できません。時としてこれでは納得できないというお客様もいらっしゃいます。
例えば病院で検査をしたときに、「あなたはこういう病気です」「でも、なぜ病気なのかはよくわかりません」と言われたらどうでしょうか。検査の精度は99.9％だと聞かされても、それで納得できるかどうかというと、それはまた別の話ではないでしょうか。
ROCKETの変数重要度の導出（当社研究）
この課題に対して、ROCKETにおいても変数重要度を “元の時系列データ” に対して導出する手法を検討し、人工知能学会の大会で発表しました。
大場 拓慈、長沼 茂太、塩澤 暁広、山下 遼人
"ROCKET特徴量を用いた多変量時系列データ分類における変数重要度の導出"
2023年度人工知能学会全国大会（第37回）
この研究内容についてご紹介します。
ROCKET特徴量はランダムに生成したものなので、元の情報はこんがらがっています。ただ、こんがらがってはいても、元の情報も含まれています。そこから逆算する形で、ROCKET特徴量に乗った重みを還元していくと、変数重要度、つまり元のデータの重要度を導き出すことができます。
なお、本研究では分類器としてリッジ回帰を用いており、さらにそのオリジナルの重要度として各特徴量の重み係数を採用しています。（他の分類器や重要度の場合にどのような結果になるかについてはさらに検討が必要です。）
以下の問題設定でこの変数重要度の妥当性を検証する実験を行いました。
人工データでの実験
データ
- 人工的に生成した時系列1000セット
- 1セットあたり5変量×長さ101
- 周期的なデータを少しずつずらしたり、ランダムな位置にノイズを加えたりしながら生成
- 全体の1/4のデータに、5つの変量（説明変数）のうち第1変数にのみパルス波がある。つまり、1,000セットの時系列データがあるなかで、200セットの第1変数にはパルス波が入っている。
分類ラベル
- パルス波の有無
こちらの図は、こちらは実験に用いた人工データのイメージです。
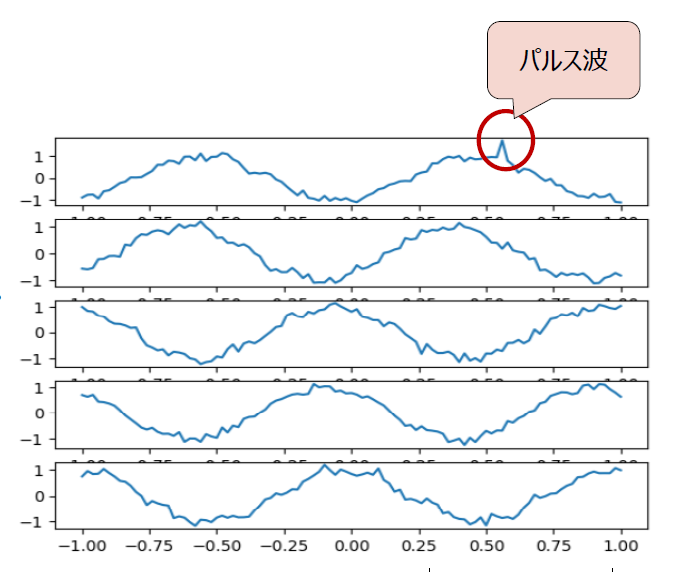
このような問題設定で、パルス波の有無の分類結果から元データの変数重要度を確認した結果がこちらです。
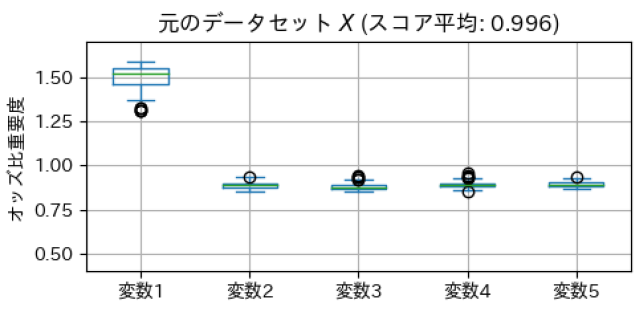
パルス波があるかどうかを分類するときには第1変数だけが重要で、残りは重要ではないという結果が出ました。このときスコア（精度）は99.6％です。 この実験では、データにランダムでノイズを入れています。学習データが少ない場合、機械学習モデルがノイズになんらかのルールを見つけてしまっていることもありえますが、モデルは第1変数にパルス波が入っていることをきちんと見分けているように見えます。
提案手法で変数重要度が高いと評価される変数が実際にスコアに寄与しているかを確認するために、第1変数の情報を排除（ゼロ埋めするのでパルス波もない）して分類してみました。
結果として、スコアは50.6％に低下しました。「パルス波があるかないかの分類問題」なので、50％というのは「コイントスをしているのと変わりない」という結果です。
この結果から、排除した第1変数（変数重要度が高いと評価された変数）のスコアに対する寄与が高いことが確認できました。
一方で、変数重要度が低いと評価される変数が実際にスコアに寄与しているかも確認するために、第2変数の情報を排除（ゼロ埋めするのでパルス波もない）した分類も行いました。
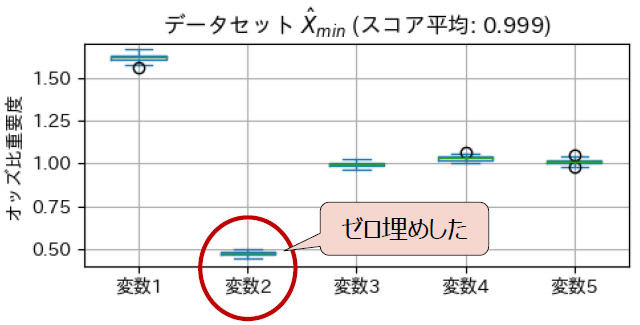スコアは99.9%で、ゼロ埋めしていない元のデータと同水準という結果でした。
この結果から、排除した第2変数（変数重要度が低いと評価された変数）のスコアに対する寄与が低いことが確認できました。
オープンデータでの実験
オープンデータ（BasicMotions）でも同様に実験を行いました。
まずは、もとのデータのまま、パルス波の有無の分類を行い、スコアと重要度を求めた結果が以下の図です。
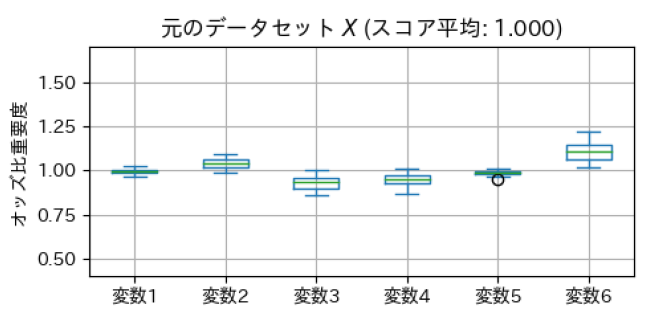
相対的に、変数2と6の重要度が高く、変数3と4が低いと評価されました。 重要度が高い変数2と6をゼロ埋めしてスコアと重要度を求めた結果が以下の図です。想定通り、スコア平均が低下し、変数2と6はスコアに寄与する変数だったことが分かりました。
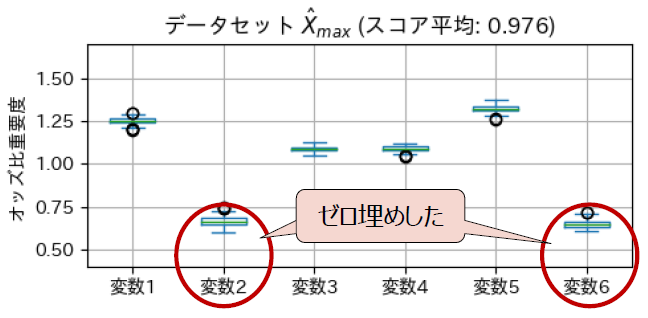
また、相対的に重要度が低い変数3と4をゼロ埋めした結果が以下の図です。この場合にはスコアは低下せず、変数3と4はスコアに寄与しない変数だったことが分かります。
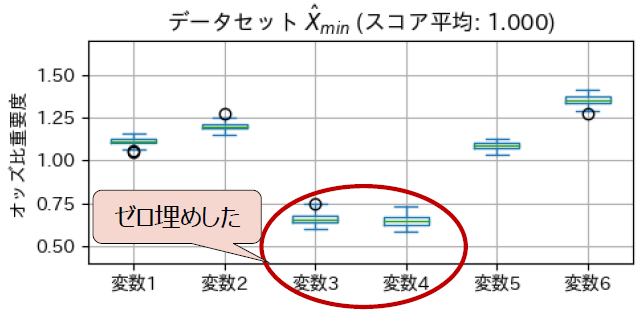
提案したオッズ比重要度は上記で検証したデータセットでは、分類に寄与する変数を見つけるための指標として妥当であることが確認できました。
このような形で重要度を確認することで、機械学習が意図通りの振る舞いをしていることが検証でき、お客様にも安心、納得していただけます。
お客様は、手元のデータのことをよくご存知です。自分たちにとって馴染みのあるデータの、どの部分がより重要なのかが機械学習によってつきとめられれば、それはおそらくお客様ご自身の感覚を裏付け、さらに深堀して考えるヒントを与えることにつながるのではないでしょうか。
その他の使いどころとしては、重要な変数がわかることで、将来のデータ収集をより効率的に行うことが可能となるでしょう。重要度でデータ収集の「コストパフォーマンス」を評価することができます。収集に高いコストがかかるが重要度が低いデータ収集は省略することを検討できます。
データについて
ROCKET を適用するための準備
既に述べたように、多変量時系列データとは、複数の関連する時系列データを一つのグループとしてまとめたデータです。例えば、スマートウォッチから取得する「歩数」、「心拍数」、「睡眠時間」などの異なるデータを同時に扱う場合、これらは「多変量」のデータとして一緒に分析されます。これを分類する際には、少なくとも「分類ラベルが付与されている」必要があります。例えば、運動している時間帯と休憩している時間帯を分類する場合、それぞれの時間帯に「運動」や「休憩」というラベルをつけます。
また、ROCKETを適用する段階では各変数のデータの長さが同じである必要があります。例えば、一つの時系列データの長さが24時間分であれば、他の変数も同時に計測された24時間分のデータが必要です。またデータは、変数ごとに一定の間隔で均等に収集されることが理想であり、不規則な収集は、モデルの誤動作を招く可能性があります。ただし、お客様がデータをお持ちいただいた時点で時間的な不整合があっても、当社側で時刻合わせなどの整合を付けられる可能性があり、また最近は（ROCKETではありませんが）不定期計測データに対応可能な手法もあります。ぜひご相談ください。
精度を上げるためのデータ品質向上
さらに、分類精度を上げるにはデータの量が十分確保されていることはもちろんですが、以下のような品質の向上も重要です。
ノイズや欠損の少なさ:
知りたいこととは無関係な変動や異常値をノイズと言いますが、これらが少ないに越したことはありません。ノイズが多すぎると、モデルがそれを手がかりとして学習を行ってしまい、汎化性能（学習データ以外が与えられたときの判別の正しさ）が下落するリスクがあります。
また、データの欠損は情報の不足であり、学習の障壁となります。欠損部分を適切に補間するか、なるべく少ないデータを選択することが重要です。
多様なデータ:
多様な状況や時期のデータを含むことで、モデルは全体像を正確に把握しやすくなります。例えば、一年を通じて売上予測を行いたいのであれば、特定の時期だけでなく、様々な日や季節、イベントを網羅した売上データによって学習させることが望ましいと言えます。
理想的なデータが準備できないときの現実的な対応
とはいえ、多様なデータを大量に用意し、正解ラベルもしっかり準備するという理想の状況の実現は現実的にとても難しい課題です。 私たちはお客様に「どんなことが知りたいか」そして「いま手元にどのようなデータがあるか」をお聞きしています。目的によって、必要なデータは変わるからです。例えば、高齢者施設で導入するシステムに、子どものデータを学習させる必要はおそらくないでしょう。
目的とデータを検討したときに「網羅性が足りない」ということがわかった場合には、まずはその状態でできることを考えます。「こういう目的で使いたい」「でも、手元にはこのデータしかない」というときに、目的にそった形に変換できる可能性もあります。
多くのデータがあればもちろん嬉しいのですが、お客様にあらゆるデータを用意していただく必要はありません。目的とデータの間にギャップがあるとき、それをどうやって埋めるのかを考えるのが、私たちの仕事です。状況を確認した結果として、「すぐに細かく分析することはできないけれど、正常か異常かを当てにいくことはできます」「それだけでもお役に立ったりしませんか？」といったご提案をすることもあります。
このように、データをどう用意するか判断するには専門的知識が求められます。何か疑問や不明点がございましたら、当社にお気軽にご相談ください。
今後の展望、意気込み
今回の研究においてROCKETの変数重要度を求められるようになり、実務上、より活用しやすくなった点は大きな意義と考えています。
ただ現状では、どの変数が重要かはわかっても、まだ、その変数のどの時間の値が重要なのかまでは特定できていません。特定の時間帯のみに発生する特徴的な波形が分類に重要なケースも想定されます。時間帯に着目した重要度判定が、「心電図で夕方に異常なパルスが発生する」ことが疾病の判別において重要であるという示唆を与え、より深い洞察をもたらすということは、十分に考えられます。
多変量時系列データをより効率的に分析できるよう、今後も研究を続けていきます。データの活用をご検討されている方は、ぜひご相談ください。
