ICLR2024 採択論文紹介: ビザンチン耐障害性を持つ新しい連合学習手法について

この記事では、株式会社NTTデータ数理システムが NTT社会情報研究所様と共同で開発した、ビザンチン耐障害性 (ビザンチン頑健性) をもつ連合学習アルゴリズムを紹介します。

本研究結果をまとめた上記の論文は機械学習分野の三大トップカンファレンスの 1 つである International Conference on Learning Representation 2024 (ICLR2024) に採択され、2024 年 5 月にオーストリア・ウィーンで発表予定です (Simple Minimax Optimal Byzantine Robust Algorithm for Nonconvex Objectives with Uniform Gradient Heterogeneity | OpenReview)。

背景

まず、背景として連合学習とビザンチン耐障害性について簡単に紹介します。
連合学習のより包括的な説明は、別の記事 (連合学習とは？Federated Learningの基礎知識をわかりやすく解説) をご覧ください。

連合学習とは何か

連合学習 (Federated Learning) は、学習データセットが分散している状況において、学習データセットを 1 カ所に集約せず分散させたまま機械学習モデルを学習する方式 の 1 つです。

学習データセットを分散させたまま機械学習モデルを学習できることの利点は何でしょうか。例えば、データセットに個人情報が含まれているケースを考えてみましょう。学習データセットを 1 カ所に集約する方式の場合、学習データセットを第三者の中央サーバーにそのまま送ることはプライバシー保護の観点で望ましくありません。これに対して、 連合学習では生のデータ情報を他者に送る必要はなく 、各クライアントが学習した機械学習モデルのみを送るだけで十分であり、プライバシー情報の漏洩リスクを減らすことができます。

連合学習が使われている例として、各 クライアント がスマートフォンのような IoT デバイス であるケースが挙げられます。例えば、Google は各スマートフォンユーザーの予測変換履歴から連合学習を用いて予測変換の学習を行っています (Federated Learning: Collaborative Machine Learning without Centralized Training Data)。

ビザンチン耐障害性とは何か

連合学習における重要な課題として、 学習に参加している一部のクライアントが悪意をもって実際の学習モデルと異なるモデルを送信 した場合、 学習全体が崩壊 してしまう、という問題が挙げられます。

例えば、クロスデバイス学習におけるスマートフォンの予測変換モデルの例では、あるユーザーがでたらめな予測変換履歴を使用した場合に、全体の学習モデルの精度が劣化することが予想されます。こうした悪意あるクライアントの攻撃は データポイズニング攻撃 (Data poisoning attack) や ビザンチン攻撃 (Byzantine attack) と呼ばれます。

このような場合に、ある一部のクライアントが (中央サーバーに気づかれずに) 異常な行動をしたとしても、全体の学習は変わらず上手くいくという頑健性 が重要になります。
頑健性のある学習アルゴリズムは、 ビザンチン耐障害性 (Byzantine fault tolerance) もしくは ビザンチン頑健性 (Byzantine robustness) という分野で盛んに研究されています。

概要

採択論文では、ビザンチン耐障害性を持つ新しい連合学習手法を提案しており、理論的に あるクラスの目的関数に対して既存手法と比べて学習誤差を小さくできる ことを示しました。また、提案手法がある意味で ミニマックス最適 であり、提案手法より優れたアルゴリズムが存在しないことも理論的に示しました。実験的にも、様々な既存手法と比べて耐障害性の観点で優位性があることも報告しました。

既存のビザンチン耐障害性アルゴリズムの課題

ビザンチン耐障害性を持つアルゴリズムの理論的な評価方法は、全クライアントのうち異常な行動を起こす可能性のあるクライアントの割合を $\delta < 0.5$ としたときに、異常なクライアントがどんな情報をサーバーに送ってきたとしてあるアルゴリズムの学習誤差が最悪でどの程度になるかを見積もるのが標準的です。

連合学習における既存の SOTA (State-of-the-art) なビザンチン耐障害性アルゴリズムとして Centered Clipping (CClip) と呼ばれる手法が提案されています。

CClip の基本的なアイディアは、各反復 $t$ について、過去の勾配情報に基づく現在の正常クライアントの平均勾配の推定量 $v$ を用いて各クライアント $i$ の勾配 $g_i^t$ を中心化し、それをある半径 $\tau$ でクリッピングし、それに $v$ を足して元に戻したものを全クライアントに関して平均してモデル更新に用いるというものです:

[[ g_{i, \mathrm{clip}}^t = v + \min\{\tau/\|g_{i}^t-v\|, 1\} (g_i^t - v) ]]

ここで、$\|g_i^t - v\|$ が $\tau$ より大きいとき、クリッピングにより差分 $g_i^t - v$ が縮小されます。$v$ は通常 1 反復前の全クライアントの補正後勾配の平均 $\frac{1}{n}\sum_{i=1}^n g_{i, \mathrm{clip}}^{t-1}$ を用います。

CClip の問題点として、理論的に最適な $\tau$ を用いた場合でも、正常クライアントの補正後勾配 $g_{i, \mathrm{clip}}^t$ にクリッピングによるバイアスが発生してしまうということが挙げられます。

正常クライアント全体を $\mathcal G$ としたとき、正常クライアントの勾配 $\{\nabla f_i\}_{i \in \mathcal G}$に関する異質性の条件

[[ \frac{1}{|\mathcal G|}\sum_{i\in \mathcal G} \|\nabla f_i(x) - \nabla f(x)\|^2 \leq \zeta^2 , \forall x \in \mathbb{R}^d ]]

を満たす目的関数クラス (これを $C_{MH}(\zeta)$ と略記します) に対して、最悪ケースでの学習誤差が $O(\delta \zeta^2)$ になることが示されています (Byzantine-Robust Learning on Heterogeneous Datasets via Bucketing | OpenReview)。

勾配の異質性 $\zeta$ はクライアント間のデータセットの特性の違いを表現したものと見ることができます。例えばスマートフォンの例ではユーザー特性の違いと見なせ、これは一般には大きな値となりえます。

つまり、 各クライアントのデータセットの特性が大きく異なる状況では、たとえ耐障害性を持っていたとしても学習アルゴリズムの学習誤差は増大 し、学習されたモデルの 予測精度低下 につながります。

提案アルゴリズム

提案アルゴリズム Momentum Screening (MS) は、スクリーニングとモーメンタムという二つのアイディアを組み合わせています。

具体的なアルゴリズムは以下になります:

以降では、上記のアルゴリズムにおける二つのアイディアについて詳しく説明します。

スクリーニング

今正常クライアント間の勾配の異質性の大きさ (つまり正常クライアント間で勾配がどれだけ離れているか) を $\zeta$ とします。

スクリーニングは、各学習反復 $t$ において以下のルールで各クライアントの勾配が正常と見なせるか否かを判定します:

以下の図は 10 クライアントの場合のこのルールの挙動のイメージになります:

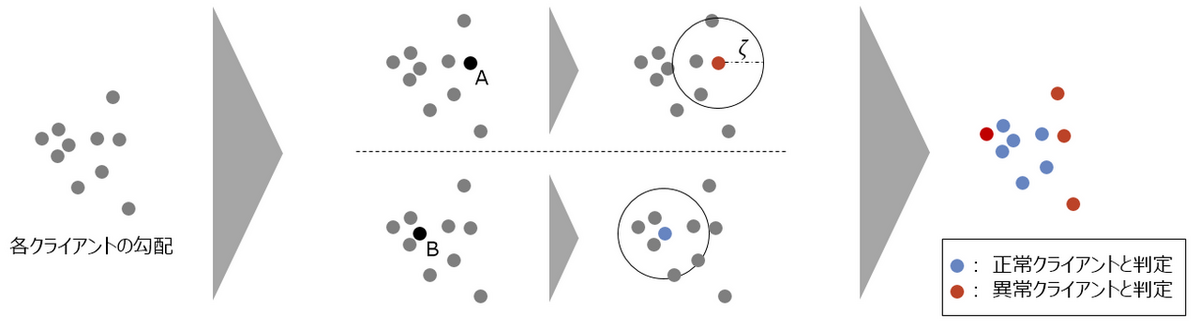
• 勾配 A の場合: 超球内に 4 ( < 5) つの勾配しかないため、異常クライアントと判定
• 勾配 B の場合: 超球内に 7 (≧ 5) つの勾配があるため、正常クライアントと判定

スクリーニング後、正常と判定された勾配のみを用いてモデルを更新します。

スクリーニングの優れた性質として、もし各クライアントの勾配にサンプリング由来の確率的ノイズがない理想的な場合、正常クライアントは常にこのスクリーニングを通過する、ということが挙げられます。

モーメンタム

モーメンタムとは、過去勾配の指数移動平均 $m_i^t=(1-α) m_i^{(t-1)}+αg_i^{t}$ を勾配 $g_i^{t}$ の代わりに利用することを指します。モーメンタムの 1 つの利点として、過去勾配の累積により確率的勾配のノイズの減少が挙げられます。

スクリーニングを勾配そのものではなくモーメンタムに適用することで、サンプリング由来の確率的なノイズに影響されにくいスクリーニングが可能です。

主結果

正常クライアントの勾配 $\{\nabla f_i\}_{i \in \mathcal G}$ に関する異質性の条件

[[ \max_{i\in \mathcal G} \|\nabla f_i(x) - \nabla f(x)\|^2 \leq \zeta^2 , \forall x \in \mathbb{R}^d ]]

を満たす目的関数クラスを $C_{UH}(\zeta)$ と略記します。このクラスは CClip が仮定していた目的関数のクラスである $C_{MH}(\zeta)$ より小さいクラスであることに注意してください。

このとき、提案法は $C_{UH}(\zeta)$ に属する $\{f_i\}_{i\in\mathcal G}$ に対して、最悪ケースでの学習誤差 $O(\delta^2\zeta^2)$ を達成することを示しました。これは、 既存法 CClip と比べて $\delta$ 倍だけ小さい学習誤差を達成可能提案法は既存法の課題であった学習誤差が大きくなってしまう問題を緩和 しています。さらに、詳細は割愛しますが、提案法は $C_{UH}(\zeta)$ においてある種のミニマックス最適性を満たす (提案法より優れたアルゴリズムは存在しない) ことを示しました。

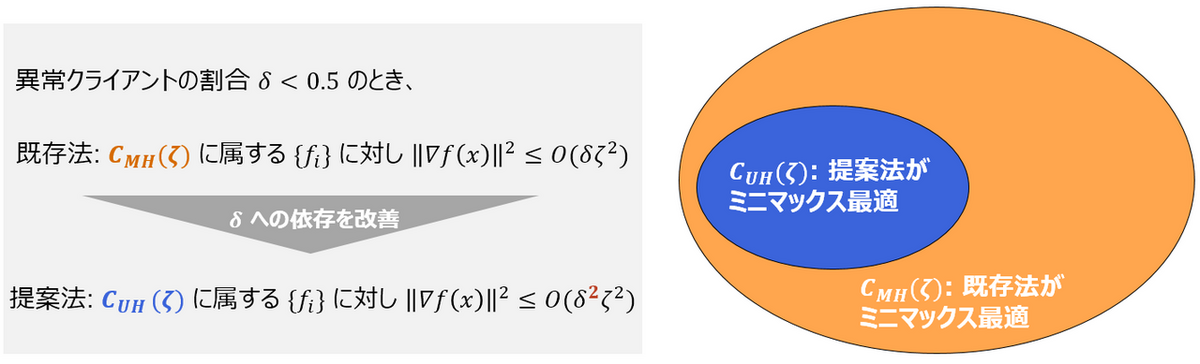
このように $\delta$ 倍だけ学習誤差が小さくできる理由としては、CClip が正常クライアントの勾配に対してもクリッピングによるバイアスが発生しうる のに対し、 MS では適切なスクリーニング半径を設定すると正常クライアントの勾配にはバイアスが一切かからない ということが挙げられます。理論上バイアス削減のためには目的関数のクラスを $C_{MH}(\zeta)$ ではなく $C_{UH}(\zeta)$ に限定する必要がある一方で、このバイアス減少分だけ学習誤差を削減でき、これが $\delta$ 倍の差になって表れていると解釈できます。

数値実験結果

既存法と提案法の性能を実験的に比較した結果が以下の表です:

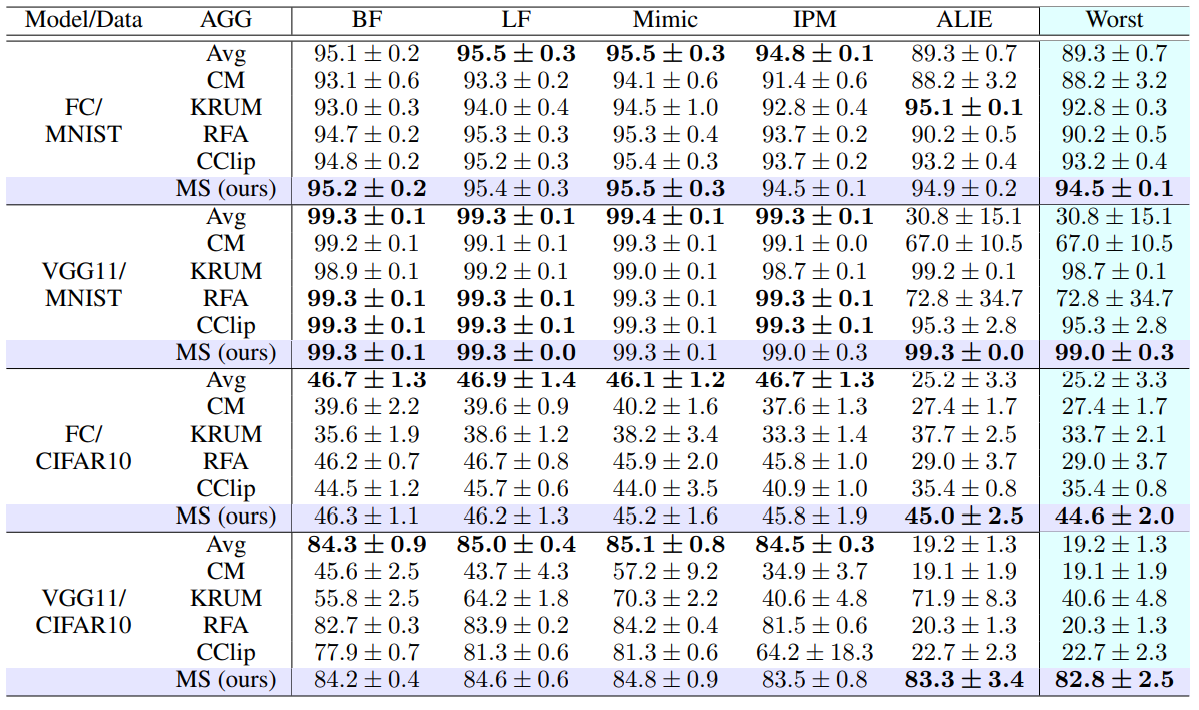
この表では、

• モデル: 2 層の全結合ニューラルネットワーク (FC)、VGG11
• データセット: MNIST、CIFAR10 (それぞれ各クライアントのデータセットが異質性を持つようにデータを疑似的に配布)

の各設定において、各学習アルゴリズム (行) の各5つの異常挙動 (列) に対する学習精度を測定しています。Worst 列は、5つの異常挙動の中で最も学習精度が低かった結果を記載しています。

この結果から、 提案法 (MS) は5つの異常挙動に対する最悪ケースの比較において一貫して最も良い性能となっている ことが分かります。

まとめ

この記事では、ICLR2024 で採択された NTT 社会情報研究所様との共著論文について紹介しました。ビザンチン耐障害性は、クロスデバイス学習のような信頼できないクライアントを含む連合学習においては欠かせない技術となりつつあります。採択論文では、クライアントの異常挙動に対して既存手法よりも頑健な手法を提案し、理論解析、実験的な評価を行い、その優位性を示しました。

NTTデータ数理システム シミュレーション＆マイニング部では、IT・通信分野のお客様への、ビザンチン耐障害性も含めた様々な連合学習アルゴリズムの研究・開発・検証支援を行った実績もございます。研究開発、実務への応用などをご検討の方はぜひご相談ください。