Numerical Optimizer V23 新機能のご紹介

  • HOME
  • Numerical Optimizer V23 新機能のご紹介

Numerical Optimizer V23 新機能のご紹介

更新日:2024年3月28日 20:47

公開日:2021年3月29日 12:00

※「Numerical Optimizer」は2022年3月28日より「Nuorium Optimizer」に名称変更しております。

2021 年の 3 月下旬に Numerical Optimizer V23 をリリースします。このバージョンでは以下の機能が追加されます。

  • PySIMPLE QP/WCSP
  • 新アルゴリズム WLS

本記事ではこれら二つの機能について紹介します。 なお、本記事で用いる用語について、"WCSP" と記した場合は問題クラスである重み付き制約充足問題を指します。 一方で "WCSP タブーサーチ" と記した場合は WCSP に特化した専用アルゴリズムを指します。

PySIMPLE QP/WCSP

PySIMPLE は Python 上で動くモデリング言語です。 C++ をベースとしたモデリング言語 SIMPLE の特徴を継承し、より使いやすくデザインされました。 PySIMPLE を用いるとデータ加工後に最適化問題を解いて結果を集計するという一連の流れをスムーズに実行することができます。 Numerical Optimizer V23 の PySIMPLE では二次式と重み付き制約充足問題を扱えます。 具体例を用いてこれらの機能をご紹介します。

PySIMPLE QP

まずは次のような問題を考えましょう。

from pysimple import *       # pysimple モジュールのインポート
p = Problem(type=min)         # 問題の定義（最小化）
x = Variable(lb=0, ub=7)      # 連続変数 x の定義
y = Variable(lb=0, ub=7)      # 連続変数 y の定義
xs = Variable(lb=0)           # 連続変数 xs の定義
ys = Variable(lb=0)           # 連続変数 ys の定義
criteria = Parameter(value=3) # パラメータ criteria の定義
p += x-criteria == xs         # 制約式の定義
p += y-criteria == ys         # 制約式の定義
p += 4*x + 7*y >= 59          # 制約式の定義
p += xs + ys                  # 目的関数の定義
p.solve()                     # x.val = 3.0000, y.val = 6.7143

連続変数 $xs$ と $ys$ は変数 $x$ と $y$ が criteria からどれほど離れているかを表します。 従ってこの問題は $4x+7y \geq 59$ という制約を満たしつつ criteria からのブレを最小化する $x$ と $y$ の値を求める問題です。 ここで、目的関数は criteria からブレたことによる罰則と解釈できます。 この問題を解くと $x=3.000$、$y=6.7143$ と求まりますが、 それぞれの変数が人の労働時間を表していた場合にこの解は役に立つのでしょうか。 $y$ の方は $x$ の方よりも 2 倍以上働くことになります。 どちらの労働負荷もなるべく同じであることが望ましいです。 そこで、基準値から離れるほど罰則が大きくなるように目的関数を二次式に変更しましょう。

p += xs**2 + ys**2           # 目的関数の定義
p.solve()                    # x.val = 4.600, y.val = 5.800

目的関数を二次式にすると $x=4.600$、$y=5.800$ となり、変数の偏りを小さくすることができました。 働きすぎていた $y$ の負荷を $x$ が肩代わりしてくれたと解釈できます。

目的関数が二次式であり、制約式が一次式の問題を二次計画問題（QP）と呼びます。PySIMPLE の例題集では二次計画問題の例として最小二乗問題とポートフォリオ最小化をご紹介しています。こちらも合わせてご覧ください。

PySIMPLE WCSP

PySIMPLE QP の例では、変数の値を criteria と一致させることが望ましいです。 しかし、$4x + 7y \geq 59$ を優先すると criteria と一致できないため、ブレの最小化をおこないました。 これを整理すると先ほどの問題は次のようになります。

  • 変数 $x$ と $y$ の値は criteria に一致させる。ただし、優先度は低い
  • 変数 $x$ と $y$ の値は制約式 $4x + 7y \geq 59$ を 必ず 満たす

このように、制約式の優先度合い（重み）が定義された問題を重み付き制約充足問題（WCSP）と呼びます。 特に Numerical Optimizer では重みに応じて制約式を次の三つに分類しています。

  • ハード制約：必ず満たすべき制約。重みが無限大
  • セミハード制約：満たすべき制約。重みは大きい
  • ソフト制約：できれば満たすべき制約。重みは小さい

PySIMPLE による WCSP の記述例は次をご覧ください。

p = Problem(type=min)                             # 問題を定義（最小化）
x = BinaryVariable()                              # 0-1 整数変数を定義
y = BinaryVariable()                              # 0-1 整数変数を定義
p += x + y == 1, "Hard", HardConstraint()         # ハード制約
p += x + y == 1, "SemiHard", SemiHardConstraint() # セミハード制約
p += x + y == 1, "Soft", SoftConstraint(1)        # ソフト制約
p.options.method = "wcsp"                         # "wcsp" または "wls" を選択する

注意として、重み付きの制約式を解釈できるのは WCSP タブーサーチアルゴリズムと WLS アルゴリズムのみです。 また、それぞれのアルゴリズムで扱える変数種別が異なります。詳細は PySIMPLE マニュアルをご覧ください。

WCSP の例としてシフトスケジューリングが挙げられます。 シフトスケジューリングでは全ての制約式をハード制約にすると実行不可能になることが多いため、 どの制約式をセミハード/ソフト制約にした計画が望ましいかという試行錯誤が必要になります。 このようなケースにおいて PySIMPLE WCSP がきっと役に立つでしょう。 また、WCSP 用のアルゴリズムは局所探索をベースにしているため、汎用的な解法である分枝限定法に比べると計算コストが小さいです。 そこで、分枝限定法では解けない大規模な問題を WCSP として定式化して解くケースも考えられます。

新アルゴリズム WLS

Numerical Optimizer V23 では重み付き局所探索法（WLS）という新しいアルゴリズムが追加されます。 このアルゴリズムは大阪大学の梅谷先生の論文[1]を参考に開発しました。 アルゴリズム自体の解説についてはマニュアルのアルゴリズム概説や論文をご覧ください。 この記事では、WCSP タブーサーチとの比較という観点から WLS を解説します。

  • S. Umetani: Exploiting variable associations to configure efficient local search algorithms in large scale binary integer programs. Eur. J. Oper. Res., Vol. 263, pp. 72-81, 2017.

探索

WLS では局所探索によって解を探索します。 具体的には現在の解 $x$ に対して k-flip という操作をおこない解を移動させます（k-flip については近傍操作で説明します）。 局所探索は計算コストが小さいというメリットがありますが、局所最適解から脱出できずに十分に良い解が得られない可能性があります。 このような事態を避けるために WCSP タブーサーチではタブーサーチを取り入れています。 タブーサーチとは直近に移動した解の情報や移動時に行った操作の記録を用いて、局所最適解からの脱出を目指す手法です。

近傍操作

WLS では k-flip という、k 個の 0-1 整数変数の値を反転させる操作で解を移動させます。 WCSP タブーサーチも同じく flip 操作で解を移動させますが、一度に flip させる変数の数に違いがあります。 WCSP タブーサーチでは一度に最大 1 つ（つまり 1-flip）、WLS では一度に最大 4 つの変数（つまり 4-flip）を変化させます。 一度に多くの変数を flip させることによって 1-flip だけでは辿り着けない解へ移動できます。 ただし、一度に flip させる変数の数が増えると計算コストも増えてしまいます。 変数組の候補を絞り込み、なるべく有望な flip のみを探索するような工夫が WLS に組み込まれています。

差分計算

近傍操作によって解を移動させるときに、 現在の解と移動先の解において目的関数と制約式の違反量がどの程度改善するかを計算します。 この計算を差分計算と呼びます。 この差分計算はアルゴリズムの計算コストの多くを占めているため高速化が重要です。 特定の問題構造に対して差分計算を高速化することはアルゴリズムを高速化する有効な手段の一つといえます。 WLS では、係数がすべて 0 か 1 である制約式に対して差分計算の高速化がなされています。 一方で差分計算の仕組みが汎用的であるほど複雑な制約式にも対応でき、扱える問題クラスが広がります。 WCSP タブーサーチはモデリング言語 SIMPLE と接続して差分値を取得する汎用的な仕組みが実装されています。 これによって、WCSP タブーサーチを SIMPLE と共に使用する場合は非線形な制約式も扱うことが可能です。

selection

selection とは $\sum_{i} x_i = 1$ という、$x_i$ のうちどれか一つだけ 1 を取る制約式を指します。 WCSP タブーサーチでは selection に特化した工夫（具体的には selection で指定された変数群を一つの変数と見なす）が組み込まれているため、selection を含む問題を得意としています。

モデリング言語との接続

WLS はモデリング言語 PySIMPLE と接続できます。WCSP タブーサーチは PySIMPLE と SIMPLE どちらとも接続できます。 差分計算のところでもお伝えしたように、SIMPLE と WCSP タブーサーチを併用すると複雑な非線形式も扱うことができます。

まとめ

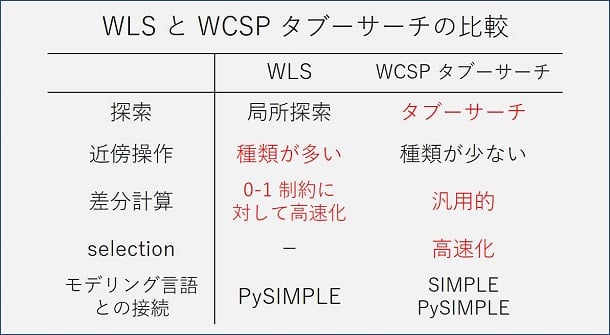
この記事では PySIMPLE QP/WCSP と WLS の解説をおこないました。PySIMPLE で QP や WCSP といった問題クラスが扱えるようになるため、より一層使いやすいモデリング言語になりました。また、WLS は WCSP タブーサーチと似たアルゴリズムですが、近傍操作や差分計算の工夫などの要所要所で違いがあります。それぞれの良いところを意識して状況に応じて使い分けましょう。

監修：株式会社NTTデータ数理システム 機械学習、統計解析、数理計画、シミュレーションなどの数理科学を 背景とした技術を活用し、業種・テーマを問わず幅広く仕事をしています。
http://www.msi.co.jp NTTデータ数理システムができること

関連記事