- HOME
- モデリング言語 RSIMPLE のご紹介
本記事では数理最適化パッケージ Nuorium Optimizer に同梱されているモデリング言語 RSIMPLE についてご紹介します。
数理最適化におけるモデリング言語とは
数理最適化におけるモデリング言語とは、人間が数理最適化問題を分かりやすく、かつ簡潔に記述するための言語です。一般的なプログラミング言語を数理最適化用に特化させたものと考えると良いです。
例えば任意の線形計画問題(LP)は標準形と呼ばれる形式に変形することができます。

この標準形に則り、以下のデータを用意することで問題を定義し、プログラムから問題の解を得ることができます。
- 目的関数を定義する配列
- 係数行列と右辺値を定義する配列
しかし、数式で記述された数理最適化問題から係数行列等のデータを用意することは煩雑で面倒な作業です。仮に用意したデータに間違いがあった場合は数式による記述と係数行列を比較する苦しいデバッグ作業が必要になります。もし数式に近い形で問題を定義してプログラムに入力することができれば、データの準備やデバッグ作業、開発後の保守がしやすくなることは明白です。
また、非線形計画問題(NLP)では一階微分や二階微分の情報が必要になります。数値データのみが与えられた場合は微分の定義を元にした数値微分により微分係数の近似値を算出しますが、数式を定義できるようになると四則演算や初等関数の関係から得られる計算グラフを元に、数式を微分した正確な式を得ることができます(自動微分と呼ばれ、深層学習の分野でも重要な技術です)。
このように、数理最適化をおこなう上でユーザーが負担になる作業を引き受け、数理最適化問題の開発に注力できるような機能が備わった言語をモデリング言語と呼びます。
Nuorium Optimizer に備わっているモデリング言語
Nuorium Optimizer にはベースとなるプログラミング言語に応じて三つのモデリング言語があります。
最初に開発された言語は C++ をベースとした SIMPLE 言語でした。集合や添字を定義することにより大規模な問題も数式と同様にかつ簡潔に記述できるという特徴を持っています。 こうした特徴は後に開発される PySIMPLE や RSIMPLE にも受け継がれています。SIMPLE では何度かの機能拡張がなされ、現在では線形計画問題、非線形計画問題、重み付き制約充足問題、資源制約付きプロジェクトスケジューリング問題、非線形半正定値計画問題というようにかなり広い範囲の問題を記述することが可能です。
PySIMPLE は Python をベースとしたモデリング言語です。Python の利便性をそのままに、SIMPLE 開発による知見を厳選して詰め込んでいるため、高速なモデル開発が可能です。 機会があれば別の記事でご紹介したいと思います。
本記事でご紹介する RSIMPLE は統計解析言語 R をベースとしたモデリング言語です。もともとは RNUOPT という別製品として販売していたものですが、Nuorium Optimizer V24 の Windows 版に同梱することになりました。こちらも SIMPLE による特徴を受け継いだ言語になっています。ここからは具体的な例題を通して記述方法をご紹介します。
ポートフォリオ最適化問題
金融資産の組合せを指すポートフォリオを利益やリスクの観点で最適化する問題を考えましょう。このような問題をポートフォリオ最適化問題と呼び、様々なリスク尺度が存在します。 ここではある程度の利益を確保して分散(リスク)を最小化するマルコビッツモデルを考えます。

目的関数 (1) は期待収益率の分散を最小化します。
制約式 (2) は期待収益率が入力した定数以上であることを意味します。
制約式 (3) は資産配分の合計が 1 であることを意味します。
制約式 (4) は各資産への組入比率が 0 以上であることを意味します。
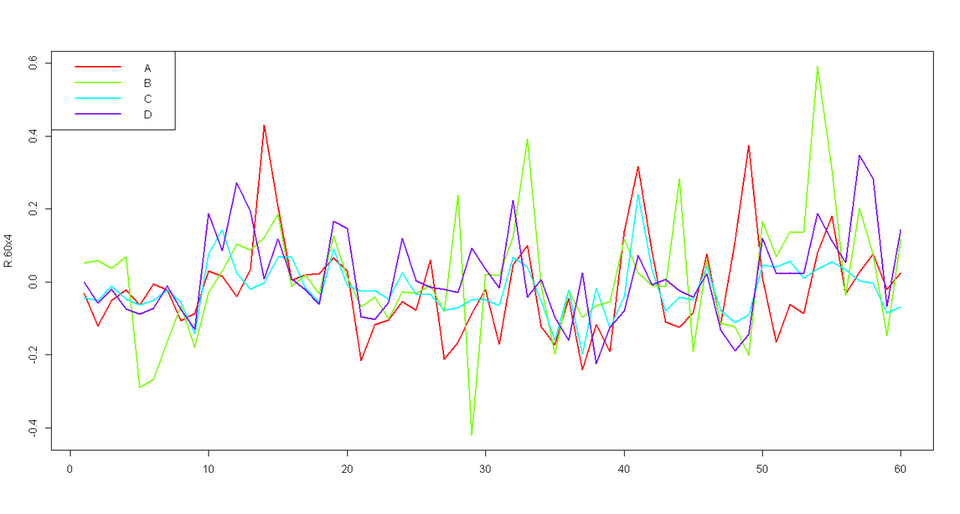
RSIMPLE による記述を紹介する前に、実際にデータを見ていきましょう。RSIMPLE には 4 銘柄の 60 期間分の収益率データ R.60x4 が同梱されています。このデータの収益率の推移、平均と分散を確認してみましょう。
> library(Rnuopt)
> var(R.60x4)
A B C D
A 0.017788838 0.005730923 0.004552905 0.003779794
B 0.005730923 0.026978759 0.005153147 0.008770707
C 0.004552905 0.005153147 0.005200091 0.004284923
D 0.003779794 0.008770707 0.004284923 0.014216287
> apply(R.60x4, 2, mean)
A B C D
-0.01483683 0.01473420 -0.01805572 0.01391076
> matplot(R.60x4, type="l", col=rainbow(ncol(R.60x4)), lwd=2, lty=1)
> legend("topleft", legend=colnames(R.60x4), col=rainbow(ncol(R.60x4)), lwd=2, lty=1)
RSIMPLE によるポートフォリオ最適化問題の記述
それでは RSIMPLE でポートフォリオ最適化問題を記述しましょう。
> Marko <‐ function(Q, rbar, rmin) {
> Asset <‐ Set() # 銘柄を表す集合
> Q <‐ Parameter(index=dprod(Asset, Asset), Q) # 収益率の分散
> rbar <‐ Parameter(index=Asset, rbar) # 収益率の平均
>
> i <‐ Element(set=Asset) # 銘柄を表す添字
> j <‐ Element(set=Asset) # 銘柄を表す添字
> x <‐ Variable(index=Asset) # ポートフォリオ
>
> risk <‐ Objective(type="minimize") # 目的関数(最小化)
> risk ~ Sum(x[j] * Q[i, j] * x[i], i, j) # ポートフォリオが与える期待収益率の分散
> Sum(rbar[j] * x[j], j) >= rmin # ポートフォリオが与える期待収益率の確保
> Sum(x[j], j) == 1 # 組入比率の合計は 1
> x[j] >= 0 # 非負制約
> }
Parameter は外部からモデルに与える入力データを定義します。今回は収益率の分散と平均を入力データにしています。
Set 及び Element は集合と添字を定義します。今回は銘柄を集合とし、銘柄を表す添字を i, j としています。
Variable は最適化によって決定する変数を定義します。今回は組入比率を変数として定義しています。
Objective は目的関数を定義しています。type=minimize によって解きたい最適化問題が最小化であることを定義しています。
残りの行では制約式を定義しています。合計を意味する Sum や添字を使うことによって、数式と似たように、かつ簡潔に記述できます。
実際に計算をするには System コマンドを用います。
> s <- System(model=Marko, var(R.60x4), as.array(apply(R.60x4, 2, mean)), 0.01)
Evaluating Marko(var(R.60x4),as.array(apply(R.60x4,2,mean)),0.01) ... ok!
[Expand Constraints and Objectives]
objective (1/4) name="risk"
constraint (2/4) name=""
constraint (3/4) name=""
constraint (4/4) name=""
> sol <- solve(s)
[About Nuorium Optimizer]
Nuorium Optimizer 24.1.1 build:ff97c72
<with META-HEURISTICS engine "wcsp"/"rcpsp">
<with Netlib BLAS>
, Copyright (C) 1991 NTT DATA Mathematical Systems Inc.
[Problem and Algorithm]
NUMBER_OF_VARIABLES 4
NUMBER_OF_FUNCTIONS 3
PROBLEM_TYPE MINIMIZATION
METHOD TRUST_REGION_IPM
[Progress]
<preprocess begin>.........<preprocess end>
<iteration begin>
res=7.6e-01 .... 9.5e-02 .... 1.1e-04 .. 9.0e-09
<iteration end>
[Result]
STATUS OPTIMAL
VALUE_OF_OBJECTIVE 0.01087261417
ITERATION_COUNT 13
FUNC_EVAL_COUNT 18
FACTORIZATION_COUNT 22
RESIDUAL 9.024786213e-09
ELAPSED_TIME(sec.) 0.01
得られたポートフォリオを確認しましょう。得られた解を確認するには current 関数に System オブジェクトと変数を与えます。
> current(s, x)
A B C D
0.07466605 0.19864172 0.06030883 0.66638339
attr(,"indexes")
[1] "*"
収益率の平均が負になっていた銘柄 A にも投資していることが確認できます。これは収益率の下限を 0.01 と小さくしているため、利益が少なくなっても分散(リスク)が最小となるポートフォリオを選んだと解釈できます。
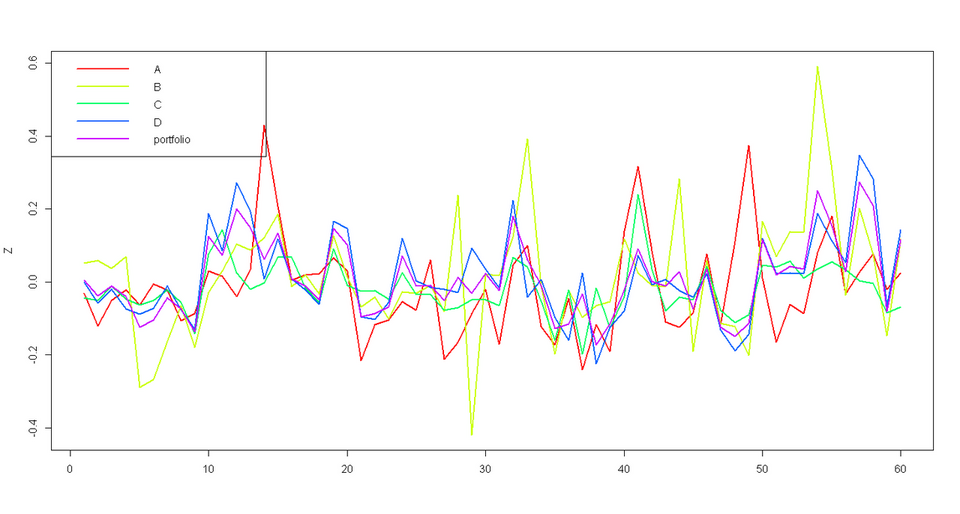
また、実際に得られたポートフォリオの収益率を銘柄の収益率のグラフに追加しましょう。
> portfolio <- R.60x4 %*% as.vector(as.array(current(s, x)))
> Z <- cbind(R.60x4, portfolio)
> colnames(Z)[5] <- "portfolio"
> matplot(Z, type="l", col=rainbow(ncol(Z)), lwd=2, lty=1)
> legend("topleft", legend=colnames(Z), col=rainbow(ncol(Z)), lwd=2, lty=1)
終わりに
いかがだったでしょうか。ポートフォリオ最適化問題を通じて RSIMPLE をご紹介しました。ご紹介したマルコビッツモデルは SIMPLE や PySIMPLE でも記述して計算をおこなうことができます。ご興味のある方はSIMPLE の例題集 や PySIMPLE の例題集をご覧ください。これらの例題では目的関数にある収益率の共分散を陽に与えないコンパクト分解表現を用いています。
http://www.msi.co.jp NTTデータ数理システムができること