Nuorium Optimizer V26 新機能を活用！重み付き局所探索法を用いた 2D Strip Packing Problem の求解

HOME
Nuorium Optimizer V26 新機能を活用！重み付き局所探索法を用いた 2D Strip Packing Problem の求解

2024年4月15日 09:00

株式会社NTTデータ数理システムは、2024/3/28 に数理最適化パッケージ Nuorium Optimizer の V26 をリリースしました。

本記事では 2D Strip Packing Problem という問題を題材に、機能強化を行った重み付き局所探索法 wls をご紹介します。

重み付き局所探索法 wls

重み付き局所探索法 wls は制約条件の重みを動的に変更しながら問題を解く局所探索法ベースのアルゴリズムです。似たアルゴリズムにタブーサーチをベースにした局所探索法 wcsp がありますが、wcsp は実行可能解を高速に得ることが得意であり、wls は良い質の実行可能解を得ることが得意です。両者の解法の詳細についてはそれぞれ以下のマニュアルをご覧ください。

重み付き局所探索法 wls の適用範囲は従来だと整数変数のみを含む問題だけでした。 V26 ではアルゴリズムに大きな改良を加えて、連続変数を扱うことが可能になりました。この改良を経て、混合整数線形計画問題 (MILP) を解く場面においても wls の活躍が期待されます。本記事では wls を用いる具体例をご紹介します。

2D Strip Packing Problem

2D Strip Packing Problem とは長方形の容器に図形を詰め込む問題です。詰め込む図形の形であったり、図形の回転を許すかなどで問題の種類が変わります。ここではシンプルに、詰め込む図形は長方形で回転を許さない問題を考えます。

2D Strip Packing Problem は実社会にも応用があり、例えば製造業におけるカッティングストック問題、 3D（三次元）で考えるとコンテナへの荷物の積み込みといった問題（※1）もあり、シンプルでありながら奥深い数理最適化問題です。

※1 例えば次のような事例があります。積付け計算・シミュレーションなど物流での数理最適化アルゴリズム開発事例｜NTTデータ数理システム (msiism.jp)

2D Strip Packing Problem の最適解を求めることは非常に難しいため、中規模から大規模な問題を解く際には専用の近似解法を実装することが一般です。ここでは、中規模な問題に対して、wls を用いるとユーザー側で細かなチューニング無しに良質な解が得られることをご紹介します。

定式化

2D Strip Packing Problem の定式化のポイントは次の三つです。

図形上端の高さの最大値を最小化すること
図形右端が容器内に収まること
図形同士が重ならないこと

図形左下の座標を $(x, y)$ とし、これら三つの条件を数式で表現[1] します。特に三つ目の条件は図形同士の位置関係からさらに四つの条件に分解することができ、それらいずれかの条件が一つ満たされることを定式化するため、四種類の 0-1 整数変数を導入します。

2D Strip Packing Problem を解く PySIMPLE コード

Nuorium Optimizer に付属している Python インターフェース PySIMPLE を用いて 2D Strip Packing Problem を記述したコードが次です。重み付き局所探索法 wls を用いるには p.solve() の前に p.options.method = Options.Method.WLS を記述します。もし、解法に分枝限定法を用いるには p.options.method = Options.Method.WLS をコメントアウトします。

引数の data には図形の幅や高さなどを格納しておき、それを Parameter というオブジェクトを通じてモデルに定義します。

from pysimple import *

def strip_packing(data):
    i = Element(value=data.items)
    j = Element(value=data.items)
    w = Parameter(index=i, value=data.width)
    h = Parameter(index=i, value=data.height)
    H_max = Sum(h[i])

    H = Variable(lb=0, ub=H_max)
    W = Parameter(value=data.W)
    x = Variable(index=i, lb=0, ub=W-w[i])
    y = Variable(index=i, lb=0, ub=H_max-h[i])

    ij = Condition((i,j), i != j)
    z1 = BinaryVariable(index=ij)
    z2 = BinaryVariable(index=ij)
    z3 = BinaryVariable(index=ij)
    z4 = BinaryVariable(index=ij)

    p = Problem()
    p += H
    p += x[i] + w[i] <= W
    p += y[i] + h[i] <= H

    p += x[ij(0)] + w[ij(0)] - x[ij(1)] <= (1-z1[ij])*W,
    p += x[ij(1)] + w[ij(1)] - x[ij(0)] <= (1-z2[ij])*W,
    p += y[ij(0)] + h[ij(0)] - y[ij(1)] <= (1-z3[ij])*H_max,
    p += y[ij(1)] + h[ij(1)] - y[ij(0)] <= (1-z4[ij])*H_max,
    p += z1[ij] + z2[ij] + z3[ij] + z4[ij] >= 1

    p.options.method = Options.Method.WLS
    p.solve()

計算実験

長方形の幅と高さを 1 ～ 10 の範囲でランダムに 40 個生成し、容器の幅を 20 として計算を行います。計算の打ち切り時間を 60 秒として分枝限定法と wls の解を確認します。

さらに、重み付き局所探索法 wls に関しては図形の数を 100 個に増やして性能を確認します。

計算環境について、OS は Windows10、CPU は Intel Core i5-13600K、メモリの性能は DDR5-4800 です。

図形 40 個の計算結果

計算を実行してから 60 秒後の解を、分枝限定法と重み付き局所探索法 wls それぞれで可視化しました。

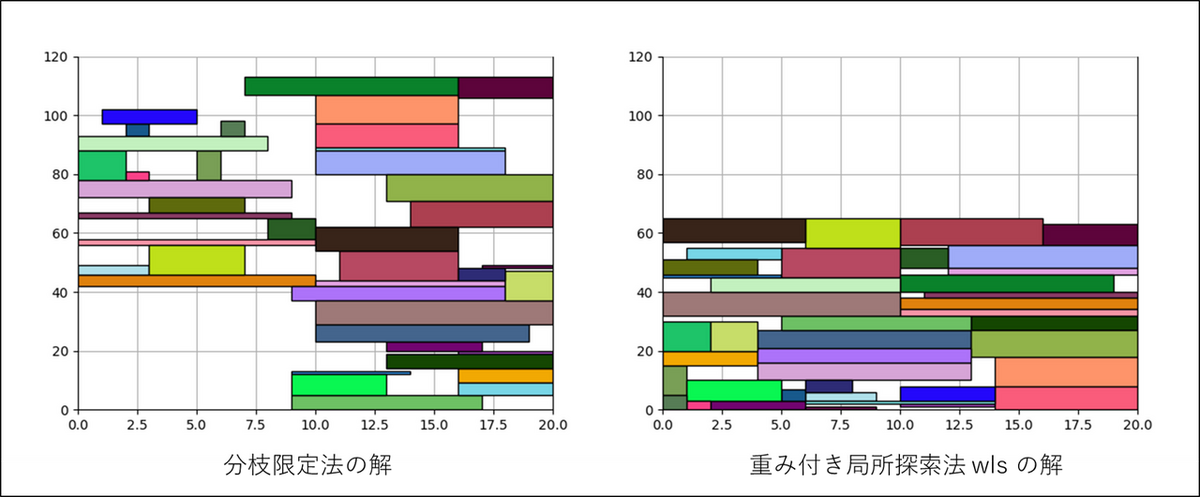
分枝限定法の解は画像を見て分かる通り、隙間があり、図形上端の高さを最小化できていないことが分かります。一方で、重み付き局所探索法 wls の方は隙間が少なく、分枝限定法に比べて良質な解が得られていることが分かります。また、60 秒後の解を可視化していますが、この解自体は 1 秒ほどで得られており、分枝限定法に対する優位性を確認できます。

図形 100 個の計算結果

さらに、中規模な問題になったときの重み付き局所探索法 wls の性能を確認します。図形の数を 100 個に増やし、容器の幅を 40 にした条件で計算を実行し、同じように解を可視化します。

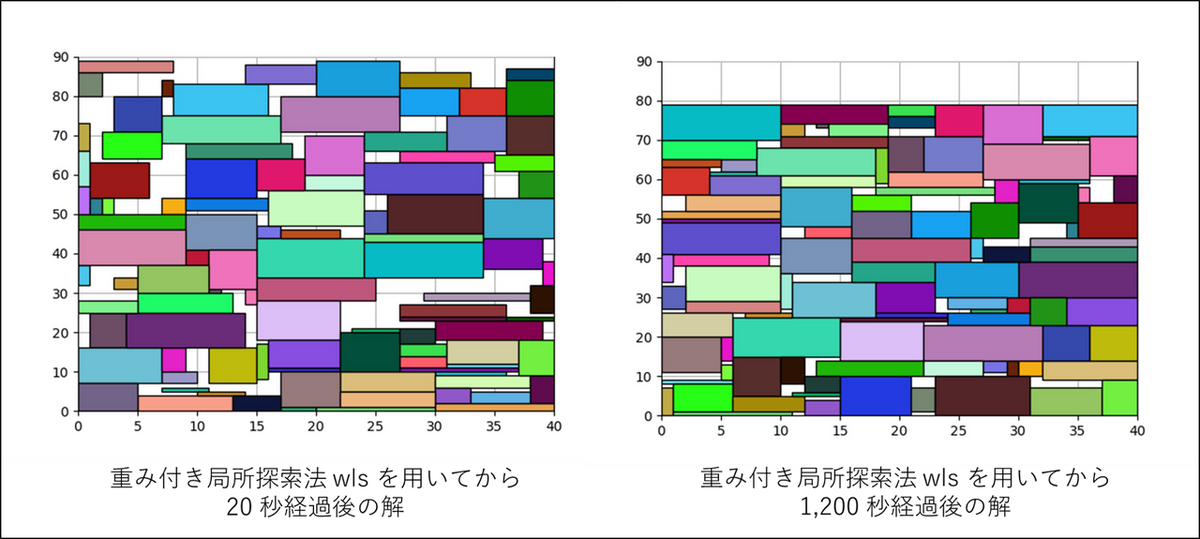
すると、計算開始後約 20 秒程で実行可能解を得ることができます。この時点の解は隙間があり、十分に良い質の解と言うには難しいです。しかし、1,200 秒まで探索を続けると隙間の少ない配置を求めることが出来ます。

終わりに

Nuorium Optimizer V26 では多くの機能が強化され、本記事では特に重み付き局所探索法 wls をご紹介しました。製品に関するご質問などございましたらお気軽にお問合せください。セミナーへのご参加もお待ちしております。

参考文献

M. Kenmochi, T. Imamichi, K. Nonobe, M. Yagiura, & H. Nagamochi. Exact algorithms for the two-dimensional strip packing problem with and without rotations. European Journal of Operational Research, 198(1):73-83, 2009.