- HOME
- 組合せ最適化ゲーム「 The Cutting Plane Game」のご紹介
更新日:2024年7月 8日 09:00
公開日:2021年11月12日 17:00
更新日:2024年7月 8日 09:00
公開日:2021年11月12日 17:00
数理計画部の藤井浩一です。
今回は The Cutting Plane Game という数理最適化に関連した Web ゲームをご紹介します。これは Gonzalo Muñoz 博士(現 O'Higgins 大学 assistant professor)が開発した、組合せ最適化の教育・普及を目的としたゲームです。
ゲームはこちらからアクセスできます。
http://www.columbia.edu/~gm2543/cpgame.html
(2021/11/11 アクセス確認)
本記事ではゲームの始め方と解説、ちょっとした攻略方法までをお伝えします。
ゲームの説明の前に、簡単に用語の説明をします。 このゲームの主役は多面体です。ゲームでは深緑色で色付けされている領域です。
多面体
影の主役は「整数点(格子点)」です。これは整数となっている点なのですがこのゲームでは、「規則正しく並んでいる点」と思えば良いでしょう。
整数点
ユーザが使う武器は「切除平面」です。切除平面は別名妥当不等式とも呼ばれ、これは整数点を切り落とすことのない平面になります。詳しくは以下の説明もご参考ください。
多面体と整数点が出てきた時点で、勘の良い方はこれが組合せ最適化問題だと気づいたかもしれません。「切除平面」は組合せ最適化問題を解く上で大変重要なツールとなっていて、このゲームのテーマはゲームを通じてこのツールを学ぶことにあります。もしピンとこないぞ、という方には、以下の記事で切除平面と組合せ最適化の関係について説明していますのでご覧ください。
ゲームの目的は、「得られている多面体に対して、切除平面( Cutting Plane)を加えることによって、可能な限りその整凸包(多面体内の整数点を含む最小の凸多面体)に近づけること」です。ちょっと難しく聞こえたかもしれませんが、要するにはユーザはどんどん切除平面を加えることにより与えられた多面体をできるだけ「整える」というゲームです。
ゲームは全部で 9 面あります。スタート画面から「 ARCADE MODE 」選ぶとゲームが始まります。真ん中に平面を加えるべき多面体が現れ、右側には利用できる切除平面の一覧が現れます。各切除平面にあらわれている数字は「切除平面を使ってよい回数」なので注意しましょう。
上手く切除平面を加えることにより、「整凸包」を得ることができれば総得点は 2 倍になります!以下の赤くなっている領域が多面体の「整凸包」になります。
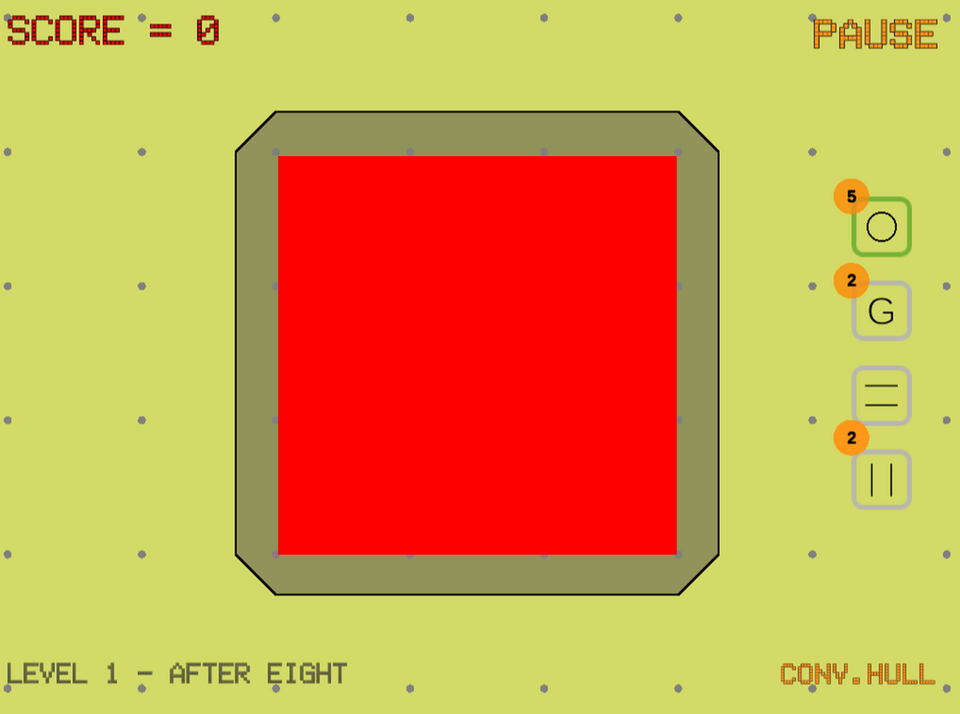
整凸包
余分な面が削られ、多面体が美しく整っているのがわかりますね。できるだけこのような理想形に近づけるのがポイントです。
切除平面達を加えていくゲームですが、切除平面は3種類用意されています。以下それぞれを解説していきたいと思います。
サークルカットは一番上から選択します。
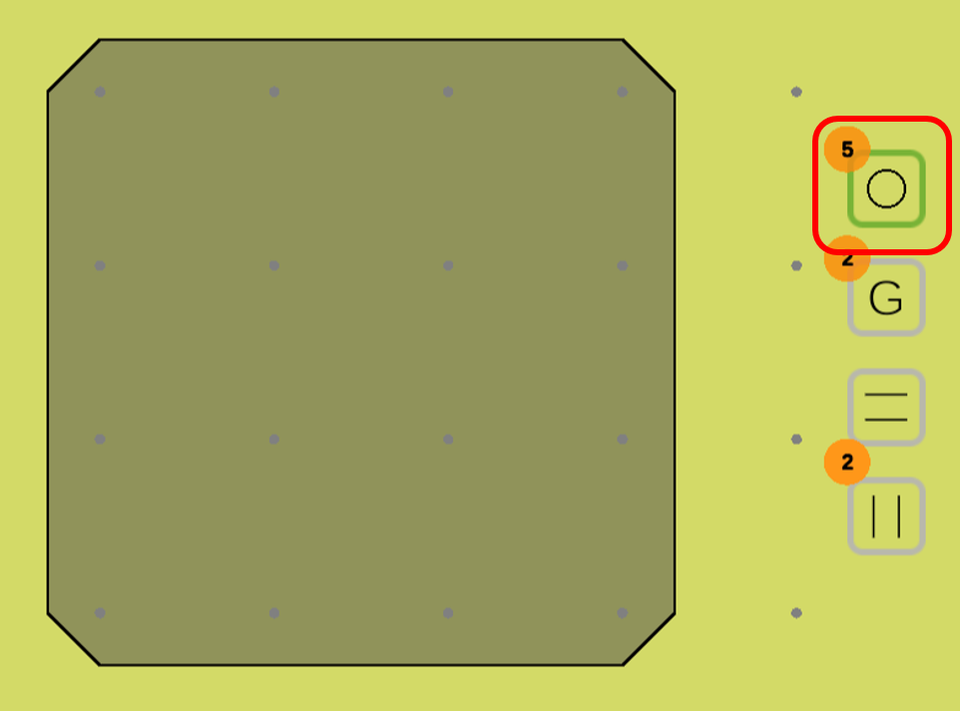
サークルカットメニュー
ユーザはまず、適当な場所をクリックします。クリックした点を中心として、円が作られます。この円は整数点までぶつかるまで、どんどん大きく成長します。ぶつかった時点で、多面体の頂点が円に含まれた場合、その頂点と円の共通部分を切り落とすような切除平面が作られます!
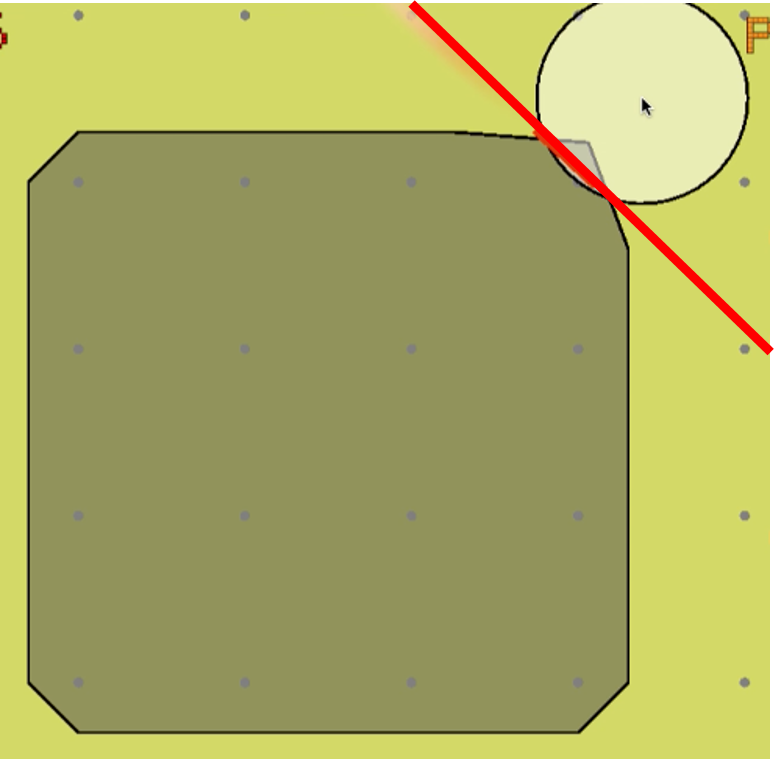
サークルカット追加
ゴモリーカットは上から二番目を選択します。
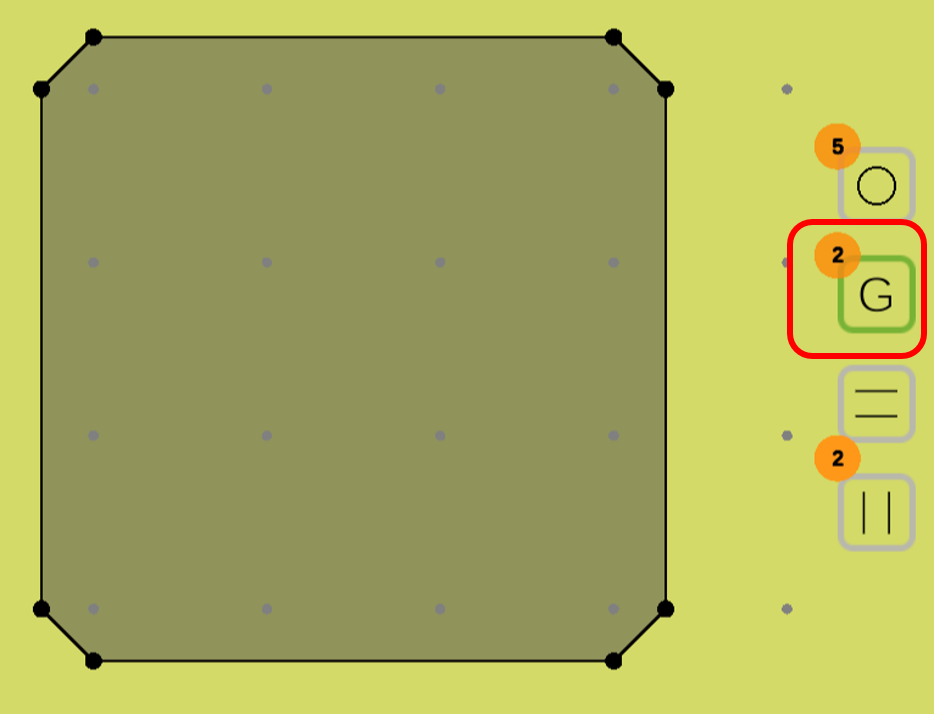
ゴモリーカットメニュー
ユーザが多面体の頂点をクリックすると、その頂点を切り落とすような切除平面が作られます。
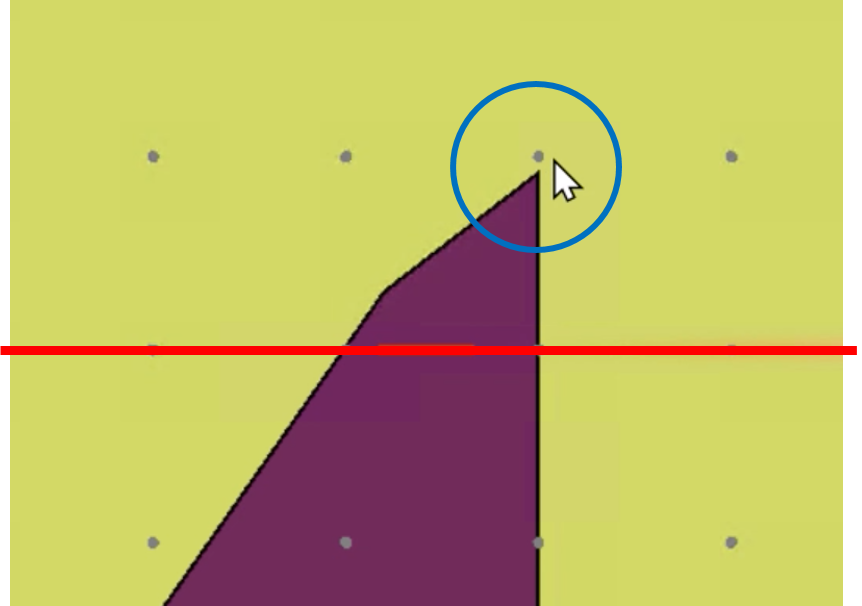
ゴモリーカット追加
スプリットカットは下部から選択できます。縦方向と横方向の二種類あるのが特徴です。
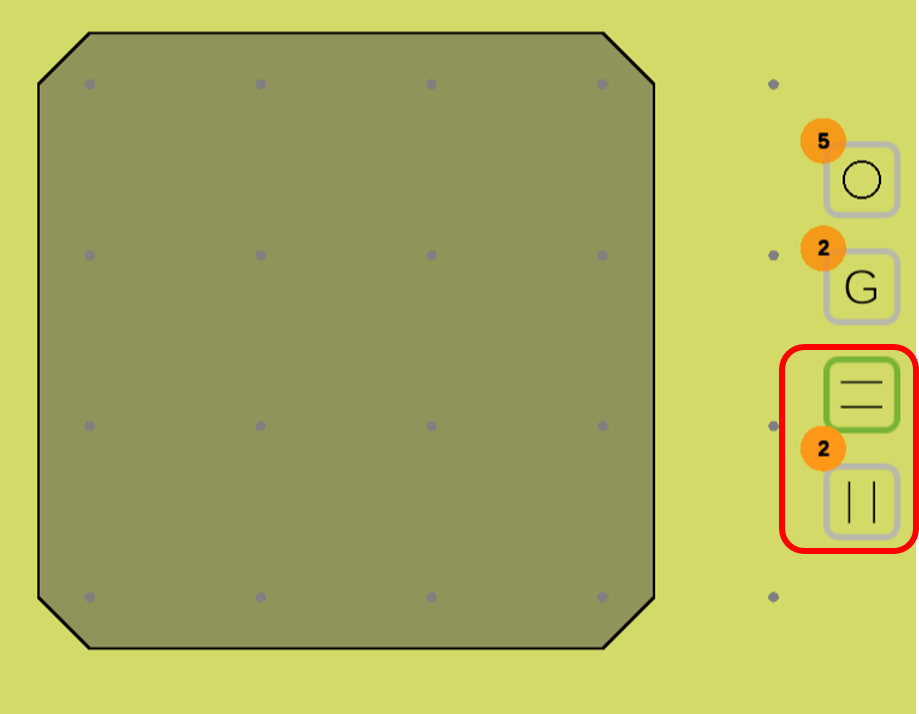
スプリットカットメニュー
ユーザは、多面体外の領域から、適当な点をクリックします。サークルカットと同様、クリックした点を中心として横方向、あるいは縦方向の長方形領域が作られます。長方形領域は整数点にぶつかるまでどんどん大きくなります。ぶつかった時点で、長方形領域と多面体領域の共通部分を切り落とすようなスプリットカットが作られます。
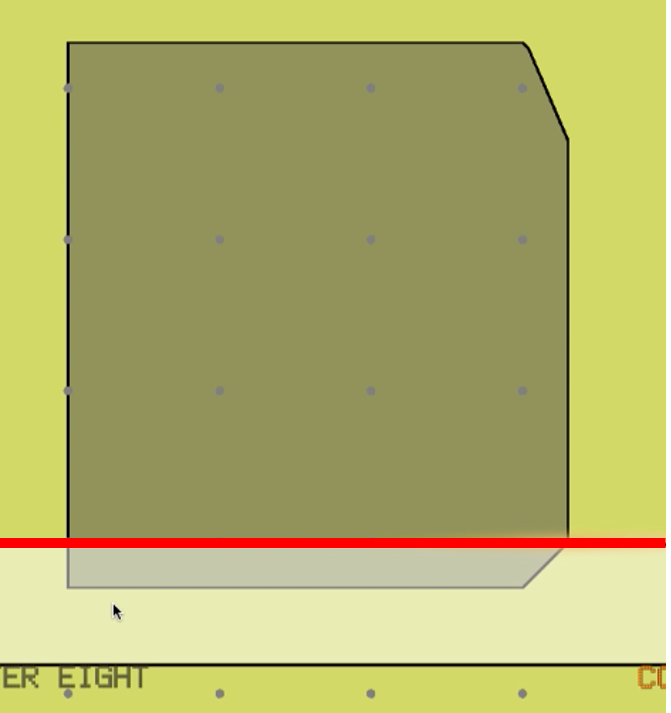
スプリットカット追加
ユーザはこれらの切除平面達を駆使して高得点を狙っていきます。
本節ではこのゲームの高得点取得方法について解説したいと思います。まずポイントは、「整凸包を得ることができれば総得点は2倍になる」というルールです。これは「総得点」は、その前までの 累積得点 です。すなわち、後半になればなるほど、整凸包を得ると飛躍的に点数が上がることになります!
どうも全ての問題で整凸包が得られるわけではないようですが、筆者がプレイした限りですと、全9面の後半に整凸包が得られる問題がありました。後半で整凸包を得ることは高得点を得る必須条件なので、じっくり探してみてください。
3種類ある切除平面の使い分けも重要です。切除平面の利用方法としては
という順番がおすすめの一つです。
最後に、スプリットカット・サークルカットはクリックする点が重要です!慎重に、整凸包を感じながらクリックをしましょう。
ちょっと珍しい、切除平面で遊ぶゲーム「 The Cutting Plane Game 」をご紹介させていただきました。 切除平面を学ぼう!という気持ちで意気込むのもよし、(私のように)数理最適化モデリングや実装で疲れた頭をほぐすのに使うもよし、いろんな遊び方があるゲームかと思います。本記事が、こちらのゲームを知って数理最適化に馴染むきっかけになれば幸いです。
私は日々の業務の中で、当社が開発している最適化ソルバー Nuorium Optimizer の速度向上に取り組んでいます。お客様から「速度向上ってどういったことをしているの?」とよく聞かれることがあり、その工夫の1つが今回ご紹介した切除平面の実装です。
このゲームではいくつかの代表的な切除平面が取り上げられていますが、他にも多種多様な切除平面があります。またソルバーへの実装にあたっては技術的な工夫も必要となってきます。ゲームをプレイすると感じられると思いますが、切除平面自体は「無限」に存在します。もちろん実装では無限に追加するわけにはいかないため,まさにゲームでされたように「回数」を制限したり,あるいは作られた切除平面から「さらに選りすぐる」必要があります。
まだまだ語りたいことはたくさんあるのですが、またの機会にしたいと思います。ここまで読んでくださった方々に感謝の意を込めて締めさせていただきます。
数理最適化・数理計画についてさらに詳しく知りたいという方は、下記のコンテンツもぜひご覧ください。



