- HOME
- Nuorium Optimizer V27 新機能のご紹介！ 重み付き局所探索法の並列計算
更新日:2025年3月12日 15:45
公開日:2025年3月12日 15:45
NTTデータ数理システムです。2025 年 3 月 に Nuorium Optimizer V27 をリリースします。 本記事では V27 の新機能である重み付き局所探索法 wls の並列計算をご紹介します。
なお、本記事では並列計算に焦点を当ててご紹介します。重み付き局所探索法 wls については次の記事をご覧ください。
重み付き局所探索法の並列計算
並列計算とは複数のプロセッサやコンピュータを用いて同時に複数の計算を行う手法です。 これにより、一般的には計算速度の高速化やより大規模な問題への対応が期待できます。
局所探索法のようなメタヒューリスティクスにおいては集中化と多様化を意識することが重要です。
- 集中化：探索空間の中で有望な点を積極的に探索すること
- 狙い：良い解の近くに更に良い解があることを期待するため
- 多様化：探索空間の異なる点を探索すること
- 狙い：局所最適解から脱出して大域最適解を探すため
Nuorium Optimizer に搭載されている重み付き局所探索法 wls は問題構造を意識して現在の解の周辺をかなり深く探索します[1][2]。 従って、集中化が意識された手法と解釈できます。 そこで、並列計算では複数のスレッドで異なる点を探索させることで多様化も確保し、より大域最適解に近い解が得られるようにします。
具体的には Nuorium Optimizer の分枝限定法の並列計算で採用されている Racing の手法[3][4]を用います。 各スレッドで異なる初期点とパラメータを持たせ（参考：下図）、並列計算させることで解空間を広く探索します。
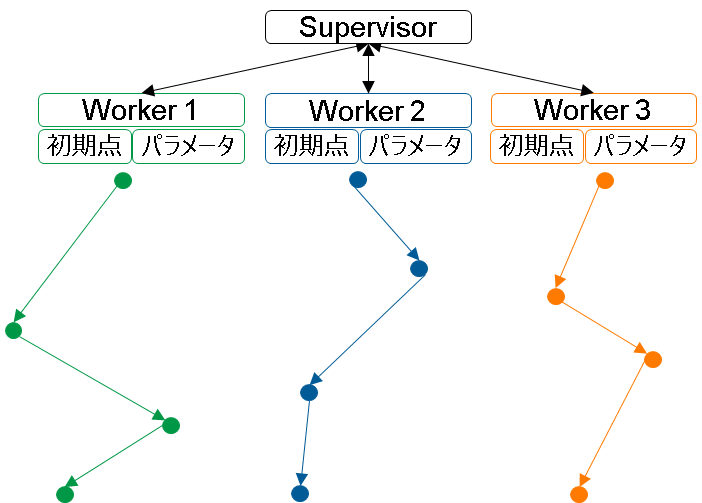
細かいところでいくつか工夫はありますが、本記事では詳細には立ち入らずに、並列計算の使い方と効果をご紹介します。
重み付き局所探索法の並列計算の利用方法
重み付き局所探索法は PySIMPLE から利用可能です。メソッドに wls を指定してスレッド数を指定します。 具体的なサンプルコードは次の通りです。
p = Problem()
# p に制約条件や目的関数を追加して問題を定義する
# ...
p.options.method = Options.Method.WLS # 解法の指定
p.options.threads = 4 # スレッド数の指定
p.solve()
適切に設定できると実行ログで Worker の数（すなわち p.options.threads で設定したスレッド数）が確認できます。
また、暫定解を更新した Worker の番号も sol: worker# の表示と共に確認できます。
具体的には次のような実行ログが得られます。
# Initial Sol = zero # Obj = -10.5 # (Hard/Soft) Penalty = 100 / 0 # Workers = 4 ---------------------------------------------------------------- Resources | Best Sol #Itrs Time(s) Mem(MiB) | Obj Hard Soft ---------------------------------------------------------------- 0 0.00 1271 | -10.5 100 0 10000 0.06 1271 | -0.5 89 0 sol: worker#1 ================================================================ # Obj = -0.5 # (Hard/Soft) Penalty = 89 / 0 # Elapsed Time(s) = 0 / 0.055 # Iterations = 3 / 10000 ================================================================ [Result] STATUS NORMAL TERMINATE_REASON End_by_iteration_limit VALUE_OF_OBJECTIVE -0.5 ITERATION_COUNT 10000 CONSTRAINT_INFEASIBILITY 89 THREADS 4 ELAPSED_TIME(sec.) 0.06 SOLUTION_FILE Problem.sol
2D Strip Packing Problem に対する並列計算の効果
実際に 2D Strip Packing Problem に対して並列計算の効果を確認します。 2D Strip Packing Problem の説明や定式化は以下の記事をご覧ください。
実験設定は容器の幅を 40 とし、100 個の長方形の幅と高さを 1.0 から 10.0 の範囲でランダムに設定します。 この設定でインスタンスを 10 個分生成します。 計算環境について、OS は Windows10、CPU は Intel Core i5-13600K、メモリの性能は DDR5-4800 です。 スレッド数を 4 とし、600 秒後の目的関数値をスレッド数 1 の結果と比較します。
| インスタンス番号 | 1 スレッド | 4 スレッド |
|---|---|---|
| 1 | 92.1 | 90.3 |
| 2 | 87.8 | 86.2 |
| 3 | 98.1 | 97.6 |
| 4 | 77.9 | 77.9 |
| 5 | 86.4 | 85.1 |
| 6 | 89.4 | 89.2 |
| 7 | 84.2 | 83.8 |
| 8 | 98.5 | 96.8 |
| 9 | 86.0 | 84.3 |
| 10 | 85.8 | 85.8 |
結果を見てみると 4 スレッドの結果は 1 スレッドの結果と同じかそれ以上の質の解が得られています。 実際にインスタンス番号 1 の結果を描画したものが次です。
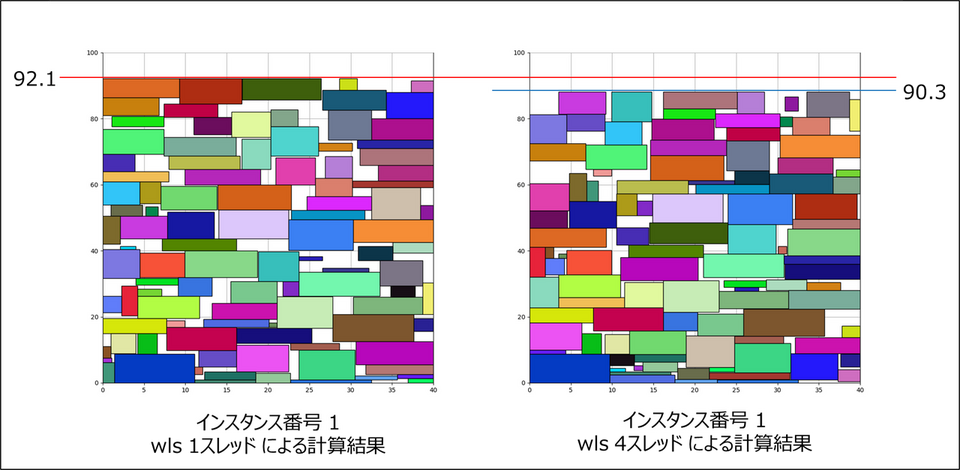
2D Strip Packing は高さを小さくするため、一見すると無関係な図形を何度も動かしていくことでようやく隙間が生まれ、高さを小さくすることができます。 これを汎用的な解法で実現することはかなり難しいことではありますが、wls では並列計算によって多様性を確保することで様々な点を探索し、性能向上を図っています。
終わりに
本記事では特に重み付き局所探索法の並列計算をご紹介しました。 製品に関するご質問などございましたらお気軽にお問合せください。セミナーへのご参加もお待ちしております。
参考文献
- S. Umetani, Exploiting variable associations to configure efficient local search in large-scale set partitioning problems, Twenty-Ninth AAAI Conference on Artificial Intelligence, February 2015.
- Nuorium Optimizer マニュアル B.6 重み付き局所探索法WLS
- Y. Shinano, et al., Solving open MIP instances with ParaSCIP on supercomputers using up to 80,000 cores. In: Parallel and Distributed Processing Symposium, 2016 IEEE International. IEEE. 2016, pp. 770-779.
- Nuorium Optimizer マニュアル B.2.4 並列分枝限定法
