物理法則を組み込んだ深層学習技術（3）～ PINNの経路計画/動作計画問題への応用

HOME
物理法則を組み込んだ深層学習技術（3）～ PINNの経路計画/動作計画問題への応用

2024年11月 7日 17:00

はじめに

前回の記事では、物理法則を組み込んだ機械学習手法の重要な一例として、Physics-informed Neural Network (PINN) [1] を紹介しました。PINN は、ニューラルネットワークを利用した偏微分方程式 (PDE) のソルバーです。PINN はニューラルネットワークを用いて解を教師値として与え教師あり学習するのではなく、ニューラルネットワークの出力が PDE を満たしていないことを損失関数とすることで、PDE を満たす関数 (=解) を学習します。現状では有限要素法などの古典的なソルバーを置き換える段階には至っていませんが、以下のメリットがあるため、盛んに研究が進められています。

PINN ではニューラルネットワークを用いて解を表現するため、有限要素法などの古典的なソルバーとの比較では、

メッシュフリーであり、有限要素法などのメッシュに基づくソルバーとは異なり、高次元の PDE を解く際も、計算量が指数的に増大しない
一度学習を済ませてしまえば、各点での解やその微分の値の計算 (推論) が高速に行える

というメリットがあります。また、同様にニューラルネットワークによる教師あり学習との比較では、

PDE 損失を用いて学習する為、教師データが不要である

というメリットがあります。これらのメリットを活かせる問題として、ロボットアームの動作計画 (motion planning) 問題を取り上げて、PINN での解法を紹介します。

本記事の構成は以下の通りです。

動作計画問題と経路計画問題の節ではまず、ロボットアームの動作計画問題とはどのような問題かを説明し、それが高次元空間における経路計画問題に帰着できることを説明します。
Eikonal 方程式と経路計画問題の節で、Eikonal 方程式を紹介し、経路計画問題の Eikonal 方程式による定式化について説明します。
PINN と動作計画問題では、動作計画問題を PINN を用いて解く一つの手法 (NTFields) について説明します。
実験の節では、動作計画のベンチマーク問題に PINN を適用して解いた結果を紹介します。

動作計画問題と経路計画問題

ロボットアーム

ロボットアームとは、人間の腕と同様に、物体をつかんで移動させるといった働きをするロボットです。ロボットアームは、複数のリンク (骨) がジョイント (関節) で接続された構造をしており、先端には、人間の手に相当するパーツであるエンドエフェクタが取り付けられています。以下に、典型的なロボットアームである UR5e [2] の CG を示します。

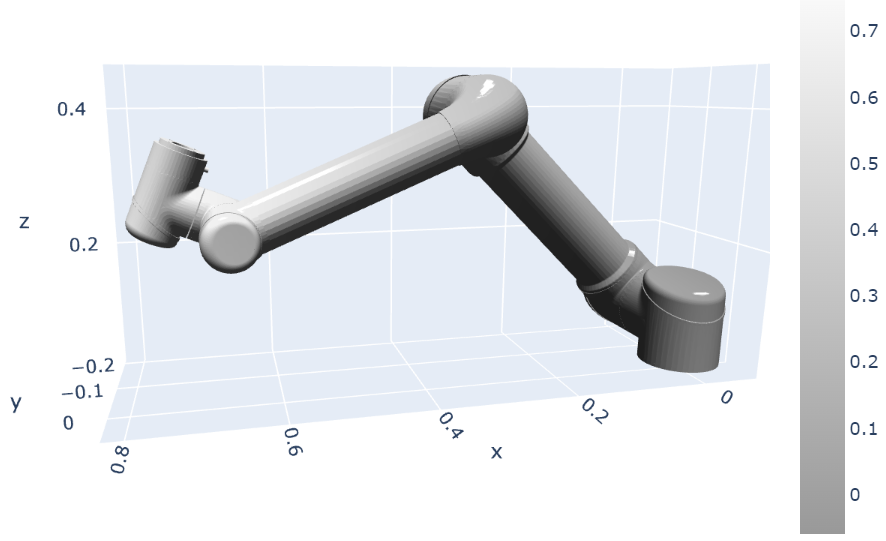
ロボットアームは、生産現場などでの事前にプログラムされた反復動作には優れていますが、新しい環境やタスクへリアルタイムに適応させることは容易ではありません。
ロボットアームの動作計画問題とは、新しい環境やタスクで、リアルタイムに、ロボットアームの姿勢を初期姿勢から目標姿勢へ、障害物を回避しながら最短で変化させる問題です。次項で動作計画問題が経路計画問題に帰着できるということを説明します。

経路計画問題としての動作計画問題

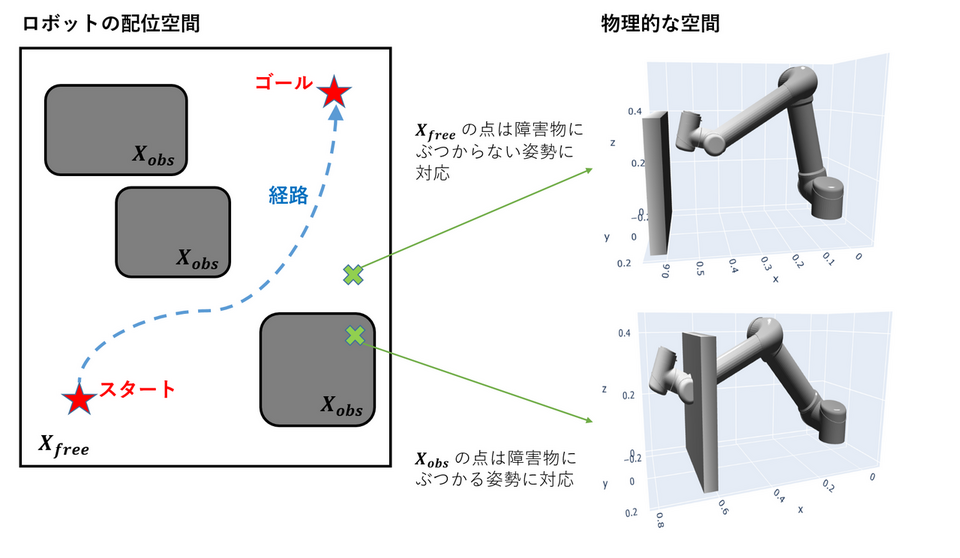
ロボットアームの姿勢は、アームの各ジョイントの回転角で指定され、ロボットアームは各ジョイントを回転させることで姿勢を変化させます。ジョイントの数 (=自由度の数) を $d$ とすると、ロボットアームの姿勢は $d$ 個のジョイントの回転角を並べた $d$ 次元ベクトル $q$ で表現されます。この空間をロボットの配位空間と呼び、 $\mathcal{X}$ と表記します。配位空間の一部の領域 $\mathcal{X} _ {obs}$ はロボットアームと障害物が接触するため実現不可能となっており、残りの空間 $\mathcal{X} _ {free} = \mathcal{X} \setminus \mathcal{X} _ {obs}$ のみが、物理的に実現可能なロボットアームの空間となっています。

ロボットアームは各ジョイントを回転させることで姿勢を変化させるので、ロボットアームの動作計画問題は、初期姿勢に対応する点 $q_s$ から、目標姿勢に対応する点 $q_g$ を結び、$X_{free}$ の範囲のみを通過する配位空間内の最短経路を求める問題に帰着されます。このような、障害物のある空間における最短経路を求める問題を経路計画 (path planning) 問題と呼びます。ロボットアームの動作計画問題は、高次元の配位空間における経路計画問題に帰着されます。

経路計画問題を解く方法はさまざまありますが、次節では Eikonal 方程式を用いた方法について説明します。

Eikonal 方程式と経路計画問題

Eikonal 方程式

Eikonal 方程式は、光の通る経路（光路）の長さ（光路長）が満たす PDE です。2 点（$x_0$、$x$）間の光路長を $L(x,x_0)$ とすると、Eikonal 方程式は以下となります。 [[ |\nabla_x L(x, x_0) | = n(x), \ L(x_0, x_0) = 0. ]] ここで、$n(x)$ は $x$ での屈折率です。第二式は $x=x_0$ での境界条件です。

Eikonal 方程式は歴史的には、光の波長が小さい場合の光の伝播の様子を、幾何学的に近似して記述する幾何光学の分野で提唱されました。幾何光学における Fermat の原理は「2 点間を通る光は所要時間が最短 (より正確には停留点) となる経路を通る」という、いわゆる変分原理の一つです。光が $x_0$ から $x$ へ伝播する際の光路は、Fermat の原理の下、光路長が最短になる経路（光路）として実現されます。この事実を PDE の形で記述したものが Eikonal 方程式となります。

Eikonal 方程式は幾何光学に由来する方程式ですが、より一般的に、空間における最短経路が満たすべき PDE として一般化することが出来ます。いま、屈折率 $n(x)$ は、真空中の光の速度 $c$ に対する媒質中の光の速度 $v(x)$ なので、$n(x) = \frac{c}{v(x)}$ を代入すると、 Eikonal 方程式は以下となります。

[[ \frac{1}{c}|\nabla_x L(x, x_0) | =\frac{1}{v(x)}. ]]

真空中の光の速度 $c$ は一定なので、$\frac{1}{c}L(x,x_0)=T(x,x_0)$ とおくと、 [[ |\nabla_x T(x, x_0) | = \frac{1}{v(x)}, ]] [[ T(x_0, x_0) = 0. ]] となります。ここで $T(x,x_0)$ は時間の次元を持ち、$x_0$ から $x$ まで移動する際の最短の所要時間を表します。$T$ を到達時間関数 (Time Fields) と呼びます。第二式は $T$ に対する境界条件です。

Eikonal 方程式を解くことで、速度場 $v(x)$ が与えられた時のスタート地点からゴール地点までの最短の所要時間（到達時間）関数 $T(x, x_0)$ が得られます。実際の経路は、到達時間関数を用いて算出する必要があります。その方法については次項で説明します。

最短経路の導出

経路計画問題は、各点での速度場 $v(q)$ が与えられた時に、スタート $q_s$ からゴール $q_g$ への最短経路を求める問題です。前述の Eikonal 方程式を解いて得られるのは、速度場 $v(q)$ が与えられた時の、（スタート地点から）ゴール地点までの到達時間関数です（なので、ゴール地点に近いほど小さな値となります）。得られた到達時間関数から最短経路を算出するには、スタート地点から始めて、到達時間関数がもっとも速く減少する方向に経路を辿ることで求めます。到達時間関数 $T(q_g, q)$ は位置 $q$ の（強化学習的な意味での）価値関数を表しており、価値の高い方向=到達時間関数の減る方向に移動することが最適な (=最短時間で $q_g$ に到達する) 方策となっています。これで正しく最短経路が求まることは、Fermat の原理 (変分原理) のもう一つの帰結です。

具体的には、到達時間関数と勾配降下法を組み合わせて最短経路を求めます。いま、スタート地点を $q_s$、ゴール地点を $q_g$ とします。$q_g$ を固定し、$T(q_g, q)$ が減少する方向に $q$ を、$q_s$ から始めて徐々に移動させます。$q$ の更新式は以下の通りとなります。 [[ q_s^{(0)} = q_s, \ q_s^{(t+1)} = q_s^{(t)} - \alpha \cdot v(q_s^{(t)}) \cdot \nabla_{q_s}T(q_g, q_s^{(t)}). \ ]] なお、$v(q_s^{(t)}) \cdot \nabla_{q_s}T(q_g, q_s^{(t)})$ は更新の方向を表す単位ベクトル、$\alpha$ が更新の幅を表すスカラー量です。これを繰り返し、$q_s^{(t)}$ が十分に $q_g$ に近づいたら更新を終了し、$(q_s^{(0)}, \cdots, q_s^{(t)})$ を最短経路として出力します。

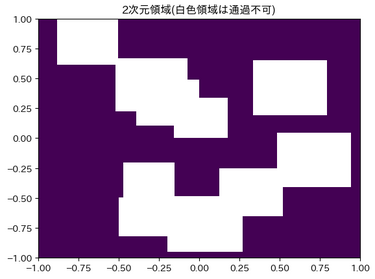
Eikonal 方程式を用いた経路計画問題の解法の例として、以下の迷路 (左端図) で 2 点を結ぶ最短経路を見つける問題を示します。

左図の紫色の領域が通行可能 ($v(q)=1$) な領域で、外壁と白抜きの領域は通過不可 ($v(q) =0$) な領域となっています。
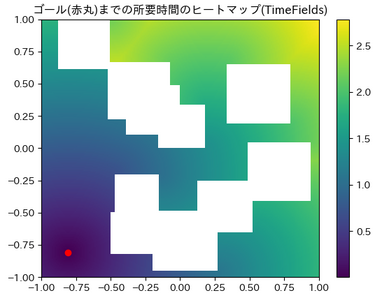
まず、Eikonal 方程式を古典的な手法である FMM [3] [4] で求解して求めた到達時間関数 $T(q_g, q_s)$ は中央図の通りとなります。ゴール $q_g$ を下図左下の赤丸の点に固定し、各 $q$ に対する $T(q_g, q)$ をヒートマップで表示しています。$(x, y)=(1, 1)$ 付近の領域や $(x, y)=(-0.5, 1.0)$ 付近の領域をスタートにすると到達に最も時間がかかっており、直感とも整合した結果になっています。
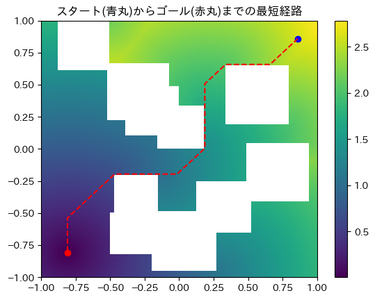
次に、勾配降下法を用いてスタート (青丸) からゴール (赤丸) への最短経路を求めた結果は右図の通りとなります。繰り返しの結果、確かに最終的にゴールに到達し、最短経路が求まっています。

PINN と動作計画問題

動作計画問題を解くには、配位空間における高次元の Eikonal 方程式を解き、求まった到達時間関数から最小時間の経路を勾配降下法などで求めます。しかし、Eikonal 方程式は、障害物のある状況では解は一意に定まらない ill-posed な問題設定であるため、そのまま PINN で解かせたのではうまく解けないことが知られています。本節では、文献[5] [6] で提案された PINN で Eikonal 方程式を解く為の工夫と、最小時間経路を求める工夫を紹介し、実際にそれらを用いて実験した結果を示します。

Eikonal 方程式を解く為の工夫

文献[5] [6] で提案された Neural Time Fields (NTFields) では、PINN を用いて障害物のある状況の Eikonal 方程式を解く為の工夫として以下を提案しています。

変数変換
対称性
粘性項
速度場
カリキュラム学習
最短経路の導出

以下にそれぞれ見ていきます。

変数変換

Eikonal 方程式の解 $T(q_g, q_s)$ は $q_s$ から $q_g$ までの所要時間を表す到達時時間関数です。始点と終点が同じ時は時間が $0$ になるという条件 $T(q_s, q_s)=0$ を明示的に課すために、$|q_g - q_s|$ を括りだし、以下とします。 [[ T(q_g, q_s) = \frac{|q_g - q_s|}{\tau(q_g, q_s)}. ]] そして、ニューラルネットワークとしては、入力を $(q_g, q_s)$ とし、出力を $\tau(q_g, q_s)$ とするアーキテクチャを用います。

対称性

到達時間関数 $T(q_g, q_s)$ および $\tau(q_g, q_s)$ は $q_g$ と $q_s$ の交換に対する対称性があります。この対称性を保証するために、NTFields においても、入力の $q_s$ と $q_g$ の入れ替えに対して出力結果が等しくなるようなアーキテクチャを用いています。具体的には max, min を取る処理を入れています。

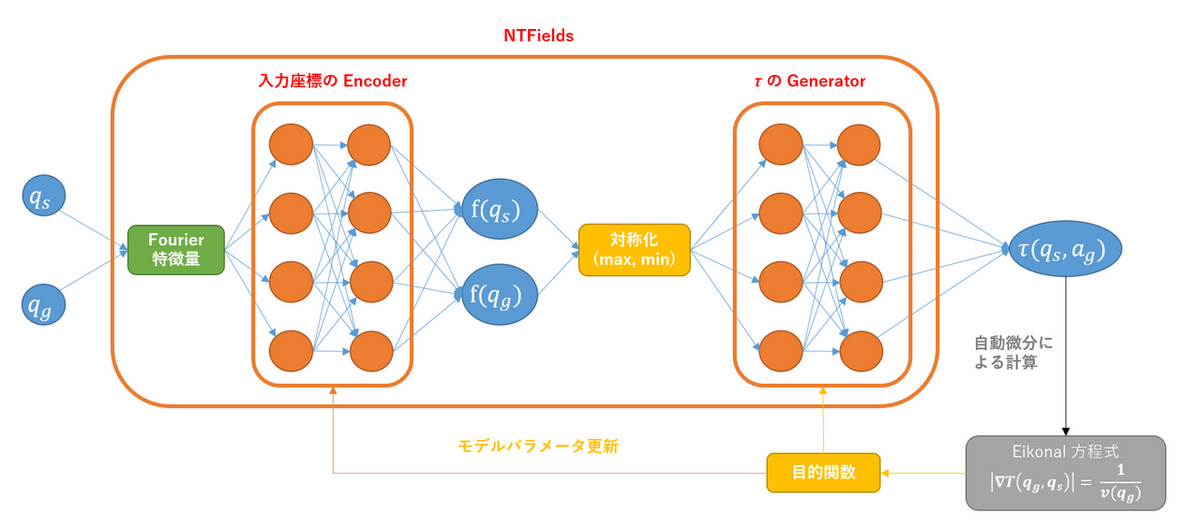
これらの工夫を踏まえて、アーキテクチャの全体図は以下の通りとなります。

まず、$q_s, q_g$ から Fourier 特徴量を作成し、エンコーダで更に特徴量 $f(q_s), f(q_g)$ に変換します。
次に、max, min による対称化処理を行います。
最後に、対称化した特徴量をジェネレータで更に変換し、$\tau(q_g, q_s)$ を出力します。

粘性項

数学的には、障害物のある状況で Eikonal 方程式の解は一意に定まらないことが知られています。Eikonal 方程式の解を一意に定めるための方法として、Eikonal 方程式に小さな粘性項を付け加えた、以下の粘性 Eikonal 方程式を用います。これは vanishing viscosity method [7] と呼ばれます。

[[ | \nabla_{q_s} T(q_s, q_g) | + \epsilon \Delta_{q_s} T(q_s, q_g) = \frac{1}{v(q_s)}. ]] 実際、NTFields では、$\epsilon$ を小さいハイパーパラメータとして粘性項を追加した Eikonal 方程式を用いることで、学習が成功しやすくなることが確認されています。

速度場

障害物のある状況で Eikonal 方程式の速度場は、$\mathcal{X} _ {obs}$ で $v=0$、$\mathcal{X} _ {free}$ で $v=1$ となり、不連続な速度場となっています。このような不連続な速度場を避けるために、速度場に以下の式で表されるクリッピングを施し、連続な場に変更します。ただし、$d_{phys}(q, \; \mathcal{X} _ {obs})$ は配位 $q$ のロボットと障害物の、物理的な空間における距離です。

[[ v(q) = \frac1{d_{max}} \text{clip}(d_{phys}(q, \; \mathcal{X} _ {obs}), d_{min}, d_{max}). ]]

カリキュラム学習

Eikonal 方程式の速度場は、障害物の付近で急速に $0$ となります。このように空間的に急激に変化する速度場を最初から学習させるのは難しいので、学習の最初は配位空間で一定の速度場からスタートし、徐々に速度場を目標とする値に近づけていくスケジューリング (カリキュラム学習) が用いられています。

最短経路の導出

Eikonal 方程式を解いて $T(q_g, q_s)$ を学習した後は、勾配降下法によって最短経路を導出します。この時、以下の 2 つの工夫を行っています。

NTFields では、前述のようにスタート $q_s$ からゴール $q_g$ に向かって経路を求めるのではなく、スタート $q_s$ と、ゴール $q_g$ からそれぞれ双方向的に経路を求めていきます。
NTFields では、障害物近くで座標の更新幅が小さくなるように、更新幅として一定の $\alpha$ でなく $\alpha v(q)$ を用いて更新を行います。

具体的には、$q_s, q_t$ 其々から、以下の更新式によって経路を求め、$|q_g^{(t)} - q_s^{(t)}|$ が十分に小さくなった時点で更新を終了し、$(q^{(0)} _ s, \cdots , q^{(t)} _ s, q^{(t)}_g, \cdots , q^{(0)} _ g)$ を最短経路として出力します。

[[ \begin{align*} (q^{(0)}_s,\; q^{(0)}_g) &= (q_s, \; q_g), \\ q^{(t+1)}_s &= q^{(t)}_s - \alpha \cdot v^2(q^{(t)}_s) \cdot \nabla_{q_s} T(q_g^{(t)}, q^{(t)}_s), \\ q^{(t+1)}_g &= q^{(t)}_g - \alpha \cdot v^2(q^{(t)}_g) \cdot \nabla_{q_g} T(q^{(t)}_g, q_s^{(t+1)}). \end{align*} ]]

実験

本節では、NTFields を用いて、実際にロボットアームの動作計画問題をシミュレーションした結果をご紹介します。

実験設定

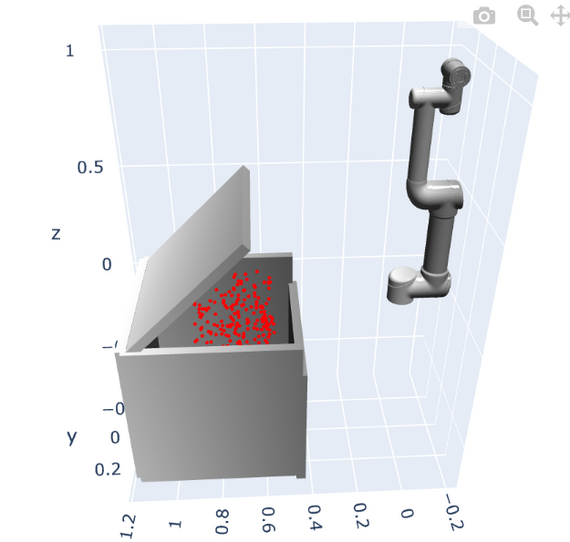
ジオメトリ：ロボットアームの動作計画問題のベンチマーク問題 [8]のセットアップの中から、障害物として蓋の空いた箱、ロボットアームとして UR5e [2] を採用
学習データ：上記ジオメトリから初期状態と目標状態をランダムに 200,000 個サンプリング
検証データ：初期状態はアームを直立させた姿勢で固定し、目標状態は、アーム先端のエンドエフェクタが箱の中に入るような配位をランダムに 200 個サンプリング
NN のアーキテクチャ
- 論文 [5] に合わせて、$q_g, q_s$ のエンコーダ⇒max処理⇒$\tau$ のジェネレータというアーキテクチャを採用した
- アーキテクチャのサイズは以下の通り
- $q_g, q_s$ のエンコーダ：幅 128、深さ 3 の ResNet
- $\tau$ のジェネレータ：幅 256、深さ 3 の ResNet
学習条件
- collocation point 数：60000
- バッチサイズ：10000
- オプティマイザ：Adam (学習率 1e-3)
- エポック数：10000
- スケジューリング：論文 [6] に同じ

初期状態および目標状態のアームのと障害物の箱を図示すると以下のようになります。散布された赤丸は、200 個の検証データの目標状態のエンドエフェクタの位置を表します。

実験結果 1

まず、実際に動作計画をシミュレーションした結果の例を示します。以下の gif の通り、箱に接触することなくアームを箱の内部に入れることに成功しています。

実験結果 2

他のアルゴリズムとの性能比較を行いました。比較対象アルゴリズムとしては、論文 [5] でも比較対象に用いられている、サンプリングベースのアルゴリズムである RRT-Connect [9] を選択しました。RRT-Connect は、ロボットアームの動作計画問題に対するデファクトスタンダードのアルゴリズムの 1 つです。性能指標を算出した結果は、以下の表の通りとなります。

手法	成功率	実行時間	経路長
NTFields	84.5%	0.06(0.04)	6.54(2.28)
RRT-connect	85.0%	0.04(0.04)	6.23(1.55)

成功率：RRT-Connect の場合、10000 回以内の反復で解を見つけられたら成功としています。NTFields の場合は、求めた経路が箱に衝突していなければ成功としています。
実行時間：両方のアルゴリズムが成功した検証データについて、経路算出までの所用時間(秒)の平均値を記載しています。括弧内の数値は標準偏差となります。
経路長：両方のアルゴリズムが成功した検証データについて、配位空間での経路長の平均値を記載しています。括弧内の数値は標準偏差となります。

上記の結果によると、RRT-Connect と NTFields はほぼ同程度の性能を持っていることが分かります。NTFields による Eikonal 方程式ベースの手法は、これに近い性能となっており、物理法則を取り入れた機械学習の経路計画への応用は、今後の発展が期待できると言えます。

おわりに

本記事では、PINN をロボットアームの動作計画問題に適用する方法を紹介しました。この問題は、一見 PDE とは関係がないように見えますが、Eikonal 方程式の求解へと帰着出来る事が知られています。特に、ロボットアームの動作計画問題は高次元の PDE になり、FMM 等の既存のメッシュベースの手法では解くのに計算量がかかります。そのため、メッシュを用いない手法である PINN が有効に機能するタイプの問題となっています。動作計画問題に限らず、高次元の PDE は PINN の有望な応用として、今後も研究が進められていくと期待できます。

次回の記事では、PINN の逆問題への応用について紹介します。