物理法則を組み込んだ深層学習技術（4）～ PINNを用いた逆問題解析（逆解析）の解法

HOME
物理法則を組み込んだ深層学習技術（4）～ PINNを用いた逆問題解析（逆解析）の解法

2024年11月26日 13:00

はじめに

前回、前々回の記事で、Physics-informed Neural Network (PINN) [1] についてご紹介してきました。これまでの記事では、数理モデル化の対象となるシステムを記述する偏微分方程式 (PDE) と初期条件や境界条件などの種々の条件が分かっている下で、PINN を用いて PDE を解く (= PDE を満たす関数を求める) という状況を想定していました。このように、PDE と種々の条件が完全に分かっている状況で、PDE の解を求める問題は PDE の順問題と呼ばれています。一方、あらかじめ PDE の解についての情報が手元にある状況で、その解を実現するような PDE や種々の条件を求める問題を PDE の逆問題 (Fig.1) と呼びます。

PINN は上記のような PDE の順問題と逆問題の両方を解くことが可能で、PINN を用いた逆問題の研究は、文献 [1] で PINN が提案されて以来、盛んに進められています。本記事では、以下の構成で PINN を用いた逆問題の解法について解説します。まず、逆問題の概観の節で逆問題とは何か、定式化と古典的な解法について解説します。次に、PINN を用いた逆問題の解法の節で、PINN を用いて逆問題を解く基本的なアイデアと工夫について解説し、実験の節で、PINN を用いて簡単な逆問題を解いた結果をご紹介します。

はじめに
逆問題の概観
- 逆問題とは
- 解法
PINN を用いた逆問題の解法
- 基本的なアイデア
- 学習の工夫
実験
- 問題設定
- 学習設定
- 結果
おわりに

逆問題の概観

逆問題とは

入力 $X$ を与えると、出力 $Y$ を得られる何らかのシステム $\mathcal A$ を考えます（$Y=\mathcal A (X)$ が成り立つとする）。このシステム $\mathcal{A}$ についての順問題、逆問題とは以下のような問題です。

順問題：入力 $X$ 、システム $\mathcal A$ がわかっている状況で、出力 $Y$ （= $\mathcal{A}(X)$ ）を求める問題。
逆問題１：出力 $Y$、システム $\mathcal A$ がわかっている状況で、入力 $X$（ = $\mathcal{A}^{-1}(Y)$ ）を求める問題。
逆問題２：入力 $X$、出力 $Y$ がわかっている状況で、システム $\mathcal{A}$ を特定する問題 (システム同定)。

逆問題の対象となるシステムには様々な例がありますが、科学や工学の分野で特に重要なものとして、

$\mathcal{A}$ が線形演算で記述される、線形システムの逆問題
$\mathcal{A}$ が PDE で記述される、PDE の逆問題

があります。以下では、これらの逆問題について説明します。

線形システムの逆問題

システムの入出力が $X$, $Y$ がベクトルであり、システム $\mathcal{A}$ が線形演算で表現できる場合が、線形システムの逆問題です。この場合、システムによる $X \to Y$ の変換を記述する方程式は、以下の一次方程式

[[ Y = \mathcal{A}X + Z, ]]

となります。$\mathcal{A}$ はベクトル $X$ に作用する行列であり、$Z$ は付加されるノイズに対応するベクトルです。観測量であるベクトル $Y$ を元に、入力ベクトル $X$ や、システムを表す行列 $\mathcal{A}$ を求める問題が逆問題となります。具体例には以下があります。

画像再構成

ボケとノイズの入った画像データから、元の綺麗な画像を復元する問題を画像再構成と呼びます。この逆問題に対して、$X$ は元々の画像のピクセル値を並べたベクトル、$Y$ は汚れた画像のピクセル値を並べたベクトル、$\mathcal{A}$ はボカしに相当する畳み込み演算の行列、$Z$ はノイズに対応するベクトルを表します。
トモグラフィック再構成

医療診断で用いられる CT スキャンは、その原理に逆問題が利用されています [2]。CT スキャンでは、物体に向けて様々な角度から X 線を照射し、物体の反対側に置かれた検出器により、物体を透過した X 線の強度分布 (投影データ) を測定します。これらの投影データ ($Y$) を元に物体の分布 ($X$) を決定する問題が、トモグラフィック再構成と呼ばれる逆問題です。

PDE の逆問題

科学や工学で現れる多くのシステムは、(一般には非線形の) PDE で記述されます。PDE の逆問題では、$X$, $Y$, $\mathcal{A}$ はそれぞれ以下に対応します。

$X$ は (1) システムに与える外場、(2) 初期・境界条件、(3) 定義域の形状、などの PDE を解く上で必要な条件です。
$Y$ は PDE を解くことで求めたい物理量です。
$\mathcal{A}$ はシステムの挙動を記述する PDE です。

この時、順問題、逆問題はそれぞれ以下の問題となります。

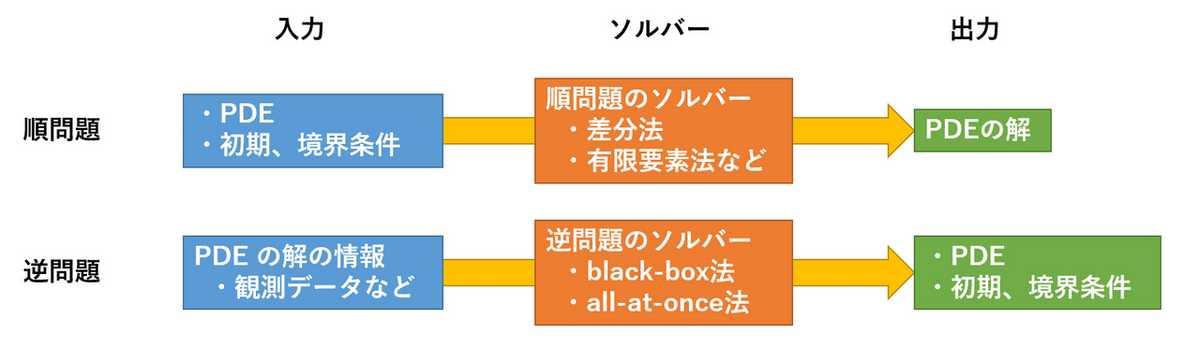
順問題：PDE $\mathcal{A}$ とそれを解くための条件 $X$ が分かっている状況で、PDE を実際に求解して解 $Y$ を求める問題。
逆問題１：PDE $\mathcal{A}$ と解 $Y$ が与えられた状況で条件 $X$ を求める問題。
逆問題２：条件 $X$ と解 $Y$ が与えられた状況で、PDE $\mathcal{A}$ （一般的には PDE そのものというよりは PDE に含まれるパラメータ）を求める問題。

特に、以下のような問題設定がしばしば現れ、重要です。

逆設計：所望の出力 $Y$ が得られるような設計変数（$X$）を求める
非破壊検査：直接観測できない量（$X$）を間接的に観測可能な量（$Y$）から推定する
パラメータ推定 (システム同定)：制御システムなどで、システムが所望の挙動を示すような条件（$\mathcal A$ のパラメータ）を求める

解法

今回の記事では、PINN の逆問題への応用に焦点を当てるため、本節では、PDE の逆問題について典型的な解法を説明します。PDE の逆問題を解く方法は、大きく以下の 2 通りに分類できます。なお、逆問題の解 (=PDE の入力やパラメータ) を $\gamma$ とし、その下での PDE の解を $u(\gamma)$ と表記します。

PDE の解 $u(\gamma)$ と逆問題の解 $\gamma$ の求解を交互に行う方法
PDE の解 $u(\gamma)$ と逆問題の解 $\gamma$ の求解を同時に行う方法

交互に求解する方法

この手法では、PDE のソルバーと、$\gamma$ を最適化するためのオプティマイザをそれぞれ別に用意して、これらを交互に適用することで逆問題を解きます。つまり、

現在の $\gamma$ の値の下で、PDE のソルバーを用いて PDE を解き、解 $u = u(\gamma)$ を求める。
解 $u(\gamma)$ が所望の条件を満たすように、オプティマイザを適用し $\gamma$ の値を更新する。

の手続きを交互に収束するまで繰り返します。$\gamma$ を最適化するためのオプティマイザには、以下のアルゴリズムが用いられます。

勾配を用いないアルゴリズム
何かしらの surrogate モデルを用いる応答局面法やベイズ最適化、遺伝的アルゴリズムなど
勾配を用いるアルゴリズム
$u(\gamma)$ の求解だけでなく、$u(\gamma)$ の $\gamma$ に関する微分・感度解析を行い、勾配降下法などを用いる手法です。ソルバーの微分・感度解析には、例えば以下のような方法があります。
- 自動微分や数値差分などを用いて数値的に微分・感度解析を行う
- 元々の PDE から、Larange 未定乗数の満たす adjoint PDE を導出し、PDE の解と adjoint PDE の解 (=Largange 未定乗数) を組み合わせて勾配計算を行う (adjoint 法 [3])。

これらの交互に求解を行う方法のメリットとして、ソルバとオプティマイザが分離しているため、各問題に応じてソルバやオプティマイザを変えられる柔軟性があります。一般的には勾配情報を用いるオプティマイザの方が効率的ですが、そのためにはソルバーで微分・感度解析が行える必要がある点には留意が必要です。これらの手法のデメリットとして、各 iteration 毎に PDE を解く必要があり、PDE の求解コストが高い場合には全体のコストが高くなります。また、$\gamma$ が最適解から遠い状況であっても PDE を解く必要があるのは、以下の同時に求解する手法と比較して非効率な場合があります。

同時に求解する方法

PDE のソルバーと $\gamma$ のオプティマイザを分離せず、逆問題を一つの制約付き最適化問題として解く方法です。文献によっては all-at-once 法とも呼ばれています。具体的には、逆問題を以下の最適化問題

[[ \min_{u, \gamma} \mathcal{J}(u, \gamma) + \lambda \mathcal{P}(u, \gamma), ]] として定式化し、この最適化問題を解く手法となります [4]。ただし、$\mathcal{J}(u, \gamma)$ は、PDE の解が目標値や観測値と食い違うことに対する罰則で、$\mathcal{P}(u, \gamma)$ は $u, \gamma$ が PDE を満たさないことに対する罰則です。

同時に求解する方法のメリットは、毎 iteration で PDE を解く必要がなく、PDE の解は最終的に最適な $\gamma$ と共に得られるため、交互に解く方法に比べて効率的な点が挙げられます。また、$(u, \gamma)$ に対する最適化問題は、交互に解く方法の $\gamma$ に関する最適化問題よりも最適化変数が高次元のため、最適解を見つけやすいこともメリットです。一方、$(u, \gamma)$ に対する最適化問題を解くには、$\gamma$ に関する最適化問題を解くよりも、多くの計算資源を消費することがデメリットです。

PINN を用いた逆問題の解法

基本的なアイデア

本節では、PINN を用いた PDE の順問題の解法について振り返り、その後で、逆問題の解法について述べます。

順問題の解法の振り返り

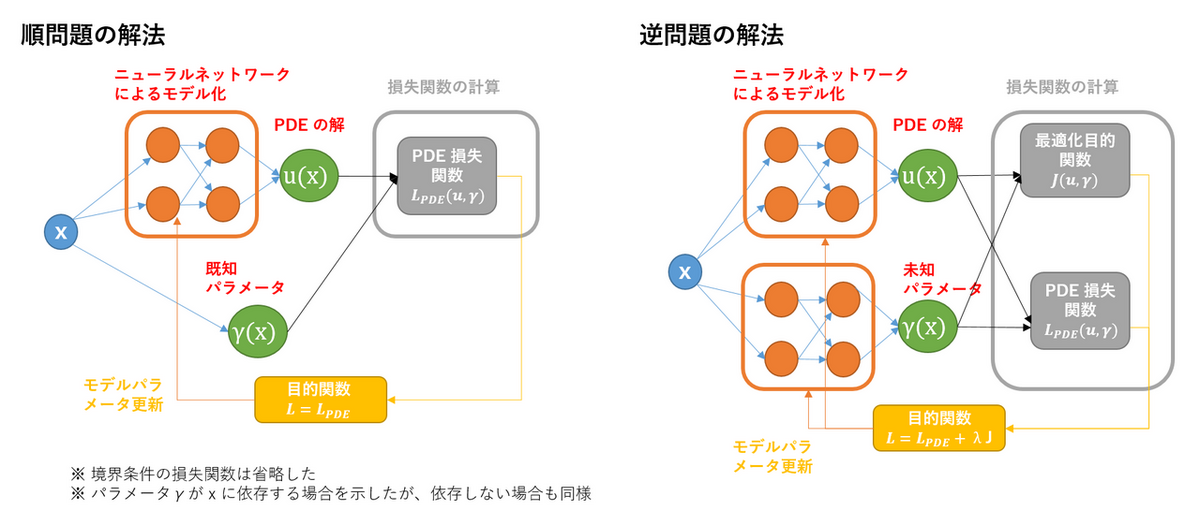
PINN を用いた順問題の解法では、$x$ を入力とし、$u(x)$ を出力とするニューラルネットワーク $u_{\theta}(x)$ を用意します。そして、ニューラルネットワークの出力が PDE を満たしていないことを損失関数 $\mathcal{L}_{PDE}({\theta})$ として、ニューラルネットワークのパラメータ $\theta$ を更新することで、ニューラルネットワークが PDE の解を学習し、順問題が解けることになります (Fig.2. 左図)。

逆問題の解法

PINN を用いた逆問題の解法では、$x$ を入力とし、$u(x)$ と $\gamma(x)$ を出力する 2 つのニューラルネットワーク $u_{\theta}(x)$ と $\gamma_{\eta}(x)$ を用意します。学習の際の損失関数としては、PDE の損失関数と、最適化の目的関数の一次結合

[[ \mathcal{L}(\theta, \eta) = \mathcal{L}_{PDE}(\theta, \eta) + \lambda_J \mathcal{J}(u_{\theta}; \gamma_{\eta}), ]]

を用いて、上記の 2 つのニューラルネットワークのパラメータを更新します。なお、$\lambda_J$ は損失関数の 2 つの項の相対的な重みを表すハイパーパラメータです。この結果、それぞれのニューラルネットワークが、逆問題の解 $\gamma(x)$ と、その時の PDE の解 $u(x)$ を学習し、逆問題が解けることになります (Fig.2, 右図)。

上記の PINN による逆問題の解法のポイントは以下の点にあります。

$u$ と $\gamma$ を何れもニューラルネットワークを用いて表現することで、勾配情報を用いた最適化に必要な勾配計算を自動微分を用いて行う。
$u$ と $\gamma$ のニューラルネットワークを、単一の損失関数を用いて同時に学習することで、PDE と逆問題の解を同時に求解する。

また、古典的な手法と比較した場合の PINN で逆問題を解くことのメリットの一つは、順問題の場合と同様にメッシュフリー性にあります。PINN では $u$ や $\gamma$ をメッシュではなく、ニューラルネットワークを用いて表現しています。そのため、古典的な手法での、高次元の問題や細かいメッシュが必要な問題に対する、計算時間やメモリ消費量の増加が緩和されることになります。もう一つは、PINN による解法は、ニューラルネットワークを用いて all-at-once に解けるというモデリングの自由度の高さもメリットとなっています。

学習の工夫

PINN では求めたい量 (順問題の場合の解、逆問題の場合の未知パラメータ) の教師値を用いずに学習を行うため、通常の教師有学習よりも学習が難しく、実際の問題を解く際には問題毎に適切な工夫を行う必要があります。PINN を用いて逆問題を解く際も、多くの場合で順問題で使われる工夫と同じ手法が有効です。具体例としては、以下の手法があります。

標本点リサンプリング
学習の途中で標本点自体を取りなおす標本点リサンプリングは、順問題だけでなく逆問題にも有効なことが確認されています [5]。
領域分割
複雑な解を持つ逆問題に対しては、定義域を分割して、其々の分割された定義域ごとに解く領域分割の手法が有効なことが確認されています [6]。
多重スケール Fourier 特徴量ネットワーク
座標 $x$ を直接入力とするのではなく、そこからランダムに作成した Fourier 特徴量をネットワークの入力とする手法は、逆問題に対しても有効です [7]。
カリキュラム学習
逆問題において、簡単な問題で学習させたネットワークを初期値として、徐々に難しい問題を学習させていくカリキュラム学習の有効性が確認されています [8]。
損失関数の重みづけ
逆問題の場合の損失関数 $\mathcal{L}$ に含まれる項 $\mathcal{J}$ と $\mathcal{L} _ {PDE}$ の相対重み $\lambda_J$ は、学習結果に影響を及ぼすハイパーパラメータです。この重みを拡張 Lagrange 法を用いて調整する方法が提案されています [9] [10]。
ハード制約化
初期条件/境界条件を、関数形を工夫することで自動的に満たす（ハード制約化する）ようにする方法です。これにより、初期条件/境界条件に対する損失を明示的に考慮する必要がなくなります [11]。
オプティマイザ
PINN のパラメータを最適化する際に、二次の最適化アルゴリズムの有効性が報告されています。例えば、Adam で学習を行った後に L-BFGS で更に追加の学習を行うと、最終的な精度が向上することが確認されています [12]。

実験

PINN の逆問題への適用例として、Poisson 方程式の逆問題に対する数値実験を行いました。平衡状態での熱分布と温度分布の関係を記述する PDE は、領域 $\Omega$ 上の熱分布 $\gamma(x)$、温度分布 $u(x)$ 、熱伝導係数を定数 $\sigma$ とすると、以下の Poisson 方程式となります。

[[ - \sigma \Delta u(x) = \gamma(x) \; \; \text{on} \;\; x \in \Omega, \ u(x) = u_b(x) \;\; \text{on} \;\; x \in \partial \Omega. ]]

ただし、第二式は境界 $\partial \Omega$ における Dirichlet 境界条件で、ここでは $u_b(x)$ は既知の関数とします。

この Possion 方程式の逆問題は、温度分布 $u(x)$ から、その温度分布を実現するような $\sigma$ や $\gamma(x)$ を求める問題で、以下の通りとなります。

逆問題１：$\sigma$ が既知の状況で、温度分布 $u(x)$ から熱分布 $\gamma(x)$ を求める問題。温度分布が観測値の場合には非破壊検査に、温度分布が目標値である場合は逆設計となります。
逆問題２：熱分布 $\gamma(x)$ が既知の状況で、温度分布 $u(x)$ から $\sigma$ を推定する問題はパラメータ推定となります。

本節では、$\sigma$ を既知として、上記の逆問題１の温度分布が観測値の場合を PINN を用いて求解した結果を紹介します。実装には PINN の python ライブラリ [13] を用いました。

問題設定

PDE
- 上記の Poisson 方程式で $\sigma=1.0$ としました。
定義域
- 定義域は正方形領域 $\Omega = [0, 1] \times [0, 1]$ としました。
境界条件
- 温度に関する境界条件として、以下の Dirichlet 境界条件を課しました。 [[ u = 0 \; \; \text{on} \; \; (x, y) \in \partial \Omega. ]]
温度の観測データ
- X 軸、Y 軸を其々 $50$ 等分したグリッド $(x_i, y_i) _ {i=1}^{2500}$ での温度データ $u_i=u(x_i, y_i)$ を観測データとして用いました。
- 観測データは以下の正解に基づいて生成しました。
正解
- 逆問題の解として、以下の温度分布と熱分布を設定しました。 [[ u(x, y) = \sin(2\pi x) \sin(2\pi y),\ \gamma(x, y) = 8\pi^2 \sin(2\pi x) \sin(2\pi y). ]]

学習設定

ネットワーク
- Dirichlet 境界条件が課された $u(x, y)$ については、以下のパラメタリゼーションを行いました。これにより、ソフト制約としての境界条件はハード制約となり、自動的に満たされます（境界条件に関する Loss を考慮しなくても良くなります）。ここで、$\tilde{u}(x, y)$ がニューラルネットワークでモデル化した関数になります。 [[ u(x, y) = x (x-1) y (y-1) \tilde{u}(x, y). ]]
- $\tilde u(x, y)$、$\gamma(x,y)$ 共に、幅 $150$、深さ $3$ の MLP（Multi layer Perceptron、多層パーセプトロン）を用いてモデル化しました。
損失関数
- 損失関数は以下としました。損失関数の第一項は、温度の観測データとの平均二乗誤差です。損失関数の第二項は Poisson 方程式を満たさないことへの罰則です。$\lambda$ は 2 つの項の相対重みのハイパーパラメータです。 [[ \mathcal{L}(\theta_u, \theta_\gamma) = \frac1N \sum_{i=1}^N || u_{\theta_u}(x_i, y_i) - u_i ||^2 + \lambda \mathcal{P}(u_{\theta_u}, \gamma_{\theta_\gamma}). ]] ここで、$u_{\theta_u}$ および $\gamma_{\theta_\gamma}$ はニューラルネットワークによる $u$、$\gamma$ のモデルで、$\theta_u$、$\theta_\gamma$ はニューラルネットワークのパラメータです。
学習方法
- バッチサイズ、collocation point 数は共に $10000$ としました。
- 学習率 $10^{-3}$ の Adam で $20000$ iter 学習後に、L-BFGS で更に学習を行いました。
評価方法
- ランダムに評価点を $10000$ 点生成し、正解の熱分布 $\gamma$ に対する平均二乗誤差で評価を行いました。
- また、参考値として、以下の指標も算出しました。
  - 上記の評価点における、正解の温度分布に対する平均二乗誤差
  - 損失関数の、観測データとの平均二乗誤差の項の値
  - 損失関数の、PDE 損失の項の値

結果

実験1：求解が可能なことの確認

$\lambda$ として $[10^{-6}, 10^{-5}, \cdots, 10^2]$ のそれぞれで学習を行ったところ、$\lambda = 10^{-5}$ で熱分布の推定が最良の性能となりました。各指標値の値は以下の通りです。観測データを用いることが出来る温度分布の方が、熱分布よりも推定精度が良くなっています。また、PDE の損失関数の値は観測データの損失関数値に比べて大きくなっています。なお、PDE の損失関数値については、重み $\lambda$ を除いた値を記載しています。

熱分布の平均二乗誤差	温度分布の平均2乗誤差	観測データの損失関数値	PDE の損失関数値
3.5%	0.086%	1.7e-7	7.8e-3

なお、熱分布の推定値と正解値は以下の通りとなり、定性的には正解値を再現できていることがわかります。

熱分布の推定値	熱分布の正解値

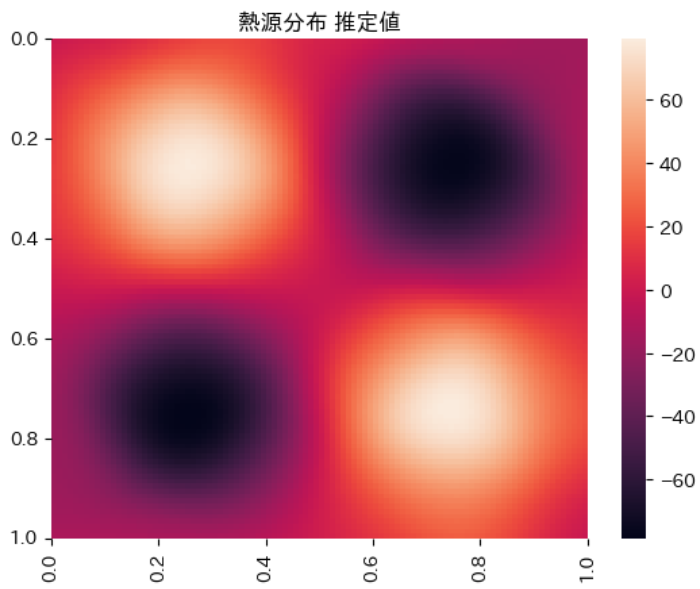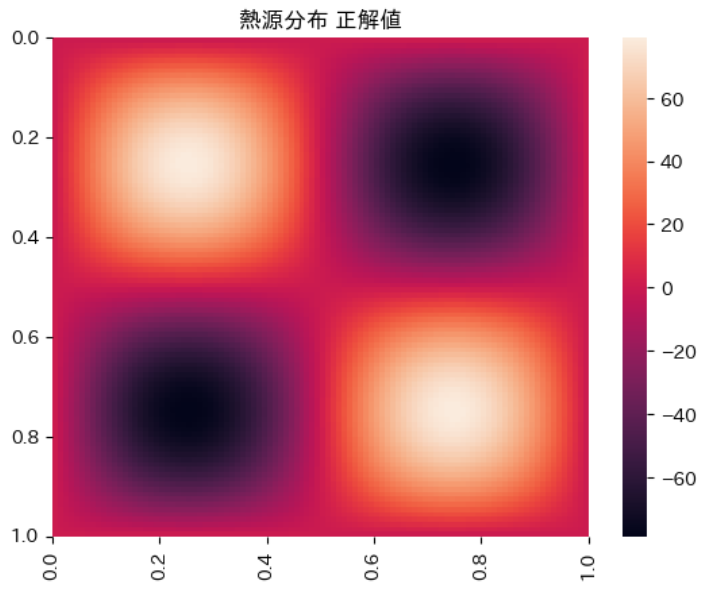実験2：拡張 Lagrange 法による $\lambda$ の調整

さらなる性能向上のために、文献 [9] の拡張 Largange 法による重み $\lambda$ の調整を行いました。拡張 Lagrange 法の設定は以下の通りとしました。

$\lambda$ の初期値：$\lambda_0 = 10^{-6}$
$\lambda$ の増加率：$\beta = 5.0$ で $\lambda_{k+1} = \beta \lambda_k$ と更新。
$\lambda$ の更新回数：最大 $10$ 回 (最も良い性能の結果を用いる)
学習方法：$\lambda_0$ での学習は Adam+L-BFGS で、$\lambda_1$ 以降の学習は L-BFGS で行う。

上記の拡張 Lagrange 法による重みの調整の結果、更新 5 回で以下の性能となりました。全ての指標値で実験１の結果を上回っており、この問題のセットアップでは、拡張 Lagrange 法による $\lambda$ の調整に効果がありました。

熱分布の平均二乗誤差	温度分布の平均二乗誤差	観測データの損失関数値	PDE の損失関数値
2.7%	0.072%	1.3e-7	2.3e-3

おわりに

本記事では、逆問題の概要と PINN を用いて PDE の逆問題を解く手法について解説し、実際に熱源の分布を推定する問題を解かせ、その結果を確認しました。順問題の場合の同様に、PINN は逆問題の古典的なソルバーを置き換えるほどには至っていませんが、基本的にメッシュフリーで、 all-at-once で解けるというモデリングの自由度などもあり、今後も PINN を用いた逆問題の研究は増えていくものと期待できます。

次回の記事では、PINN を用いた逆問題の解法の、より現実的な応用事例への適用をご紹介します。