物理法則を組み込んだ深層学習技術 (2) ～ PINNの紹介

HOME
物理法則を組み込んだ深層学習技術 (2) ～ PINNの紹介

2024年2月19日 13:00

はじめに

前回の記事でご紹介したように、科学技術分野に機械学習技術を応用する際の手法として、物理法則を組み込んだ機械学習手法 (Physics-informed Machine Learning, PIML) が注目を集めています。PIML は、対象とするシステムが従うことが分かっている物理法則を事前知識 (prior knowledge あるいは inductive bias) として組み込んで機械学習モデルを作成する手法の総称です。

多くのシステムにおいて、物理法則は偏微分方程式 (Partial Differential Equation, PDE) の形式で記述されています。与えられた境界条件・初期条件のもとで PDE を解くことで、システムの挙動を解析することが出来ます。しかし、実際のシステムで PDE を満たす関数を解析的に求められることは稀で、通常は有限差分法、有限体積法、有限要素法といった数値解法を用いて近似的な解を求めることになります。ニューラルネットワークには任意の関数を近似できるという性質 (万能近似性) があります。PIML の一例である Physics-informed Neural Network (PINN) [1] は、PDE を満たす関数を学習することで PDE を数値的に解きます。

PIML について概説した前回の記事の続編として、本記事では、以下の構成で PINN についてご紹介します。

PINN の基本的なアイデア
PINN のメリット・デメリット
PINN の failure mode - 移流方程式を例として
PINN の failure mode を防ぐ工夫

PINN の基本的なアイデア

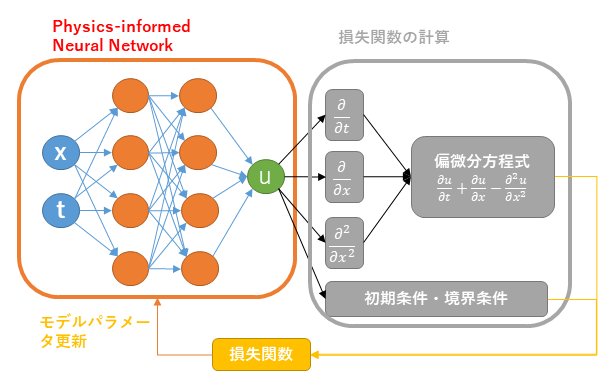
本節では PINN の基本的なアイデア (Fig.1) を解説します。

PINN は PDE の解をニューラルネットワークでモデル化し、ニューラルネットワークの学習によって PDE を求解する PDE ソルバーです。PINN のニューラルネットワークは、PDE の独立変数 (空間座標や時刻等) を入力とし、その独立変数の値での解の値を出力します。ネットワークアーキテクチャは、通常は多層パーセプトロンが用いられますが、CNN や RNN、トランスフォーマーが用いられる場合もあります。

PINN は、学習 = PDE の求解、となるように特殊な損失関数を用いて学習を実行します。損失関数は、ニューラルネットワークの出力が初期条件、境界条件、PDE のそれぞれを満たすほど値が小さくなり、満たさないほど値が大きくなるように、以下の数式で定義します。まず PDE を

[[ \begin{aligned} \mathcal{F}[u](t, x) &= 0 \\ \mathcal{B}[u](t, x_b) &= 0 \\ \mathcal{I}[u](t=0, x) &= 0 \end{aligned} ]]

と表記します。ここで、 $u(t, x)$ は PDE の解、$\mathcal{F}$ は $\mathcal{F}[u] = \frac{\partial u}{\partial t} + \frac{\partial u}{\partial x} - \frac{\partial^2 u}{\partial x^2} $ などの PDE を表す微分演算子です。$\mathcal{B}$ は境界上の点 $x=x_b$ での境界条件を、$\mathcal{I}$ は初期値 $t=0$ での初期条件を表します。この時、PINN の最適化に用いられる損失関数は以下の形になります。

[[ \begin{aligned} \mathcal{L} &= \lambda_r \mathcal{L}_r + \lambda_b \mathcal{L}_b + \lambda_i \mathcal{L}_i \\ \mathcal{L}_r &= \frac1{N_r}\sum_{k=1}^{N_r} |\mathcal{F}[u](t_k^{(r)}, x_k^{(r)})|^2 \\ \mathcal{L}_i &= \frac1{N_i}\sum_{k=1}^{N_i} |\mathcal{I}[u](t_k^{(i)}=0, x_k^{(i)})|^2 \\ \mathcal{L}_b &= \frac1{N_b}\sum_{k=1}^{N_b} |\mathcal{B}[u](t_k^{(b)}, x_k^{(b)})|^2 \end{aligned} ]]

ただし、

${t_k^{(r)}, x_k^{(r)}}_{k=1}^{N_r}$ は PDE の定義域の内部からサンプルした標本点
${t_k^{(i)}=0, x_k^{(i)}}_{k=1}^{N_i}$ は $t=0$ の初期状態からサンプルした標本点
${t_k^{(b)}, x_k^{(b)}}_{k=1}^{N_b}$ は定義域の境界からサンプルした標本点

です。損失関数 $\mathcal{L}_r, \mathcal{L}_i, \mathcal{L}_b$ はこれらの標本点でどの程度 PDE、初期条件、境界条件が満たされているかをそれぞれ定量化した値となっています。 $\mathcal{L}_r, \mathcal{L}_i, \mathcal{L}_b$ の重み付き平均である $\mathcal{L}$ を最小化することで、PDE、初期条件、境界条件の全てを (近似的に) 満たす PDE の解をニューラルネットワークが表現するようになります。なお、これらの損失関数の値を計算し、学習を進めるうえで、解 $u(t, x)$ の正解データは必要でなく、(通常の PDE ソルバーと同様に) PDE の具体的な表式および初期条件・境界条件が分かっていれば十分です。

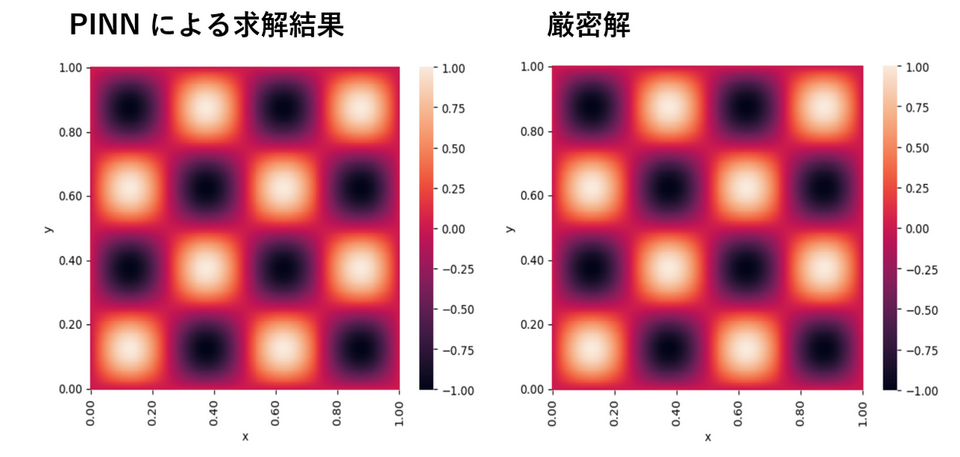
実際に PINN を用いて具体的な PDE の解を求めた結果は以下のようになります。Fig.2 では、時間依存性のない PDE の境界値問題として、定常波に対する波動方程式である Helmoholtz 方程式を PINN で求解し、厳密解 $u(x, y) = \sin(4\pi x) \sin (4\pi y)$と共に図示しています。PINN で求まった解の厳密解との平均相対二乗誤差は 0.5 % 未満であり、良好な精度で PDE を求解出来ています。

[[ - \frac{\partial^2 u}{\partial x^2} - \frac{\partial^2 u}{\partial y^2} - (4\pi)^2 u = (4\pi)^2 \sin(4\pi x) \sin (4 \pi y), \\ x\in [0, 1], \; y \in [0, 1], \\ u(x=0, y) = u(x=1, y) = 0, \\ u(x, y=0) = u(x, y=1) = 0. ]]

PINN のメリット・デメリット

PDE の解を求める手段として、既に有限差分法、有限体積法、有限要素法などを用いた様々なソルバーが開発されています。これらの通常の PDE ソルバーと比較して、PINN によるソルバーには以下のメリットがあります。

一つ目のメリットは、深層学習は原理的には入力と出力の間のどのような複雑な関係性もモデル化できる点 (深層学習の万能近似性) です。現実世界の PDE の問題では、複数の変数が複雑に相互作用しながら時間変化しており、このような系は複雑な関数になることが予想されます。

二つ目のメリットは、通常のソルバーでの求解が難しい高次元の PDE にアプローチできる点です。有限要素法などの PDE ソルバーは、求解の際にメッシュを生成し、PDE をメッシュ上での線形方程式の問題に変換します。計算時間はメッシュのノード数に大きく依存するため、ノード数が必然的に大きくなる高次元の PDE をこれらのソルバーで解くことは現実的ではありません。PINN はニューラルネットワークが連続的な時空座標を入力として受け付けるため、メッシュを用いる必要がなく、上記の計算量の問題は緩和されます。実際、画像処理や自然言語処理での成功から、深層学習は高次元のデータに強いと考えられています。

最後のメリットは、PINN は順問題を解く場合と、実装を大きく変えずに逆問題を解くことが出来る点です。通常の PDE ソルバでパラメータなどを推定する場合には、PDE の求解とパラメータの推定の bi-level の最適化問題を解く必要があります。PINN で逆問題を解く際には、PDE の解をモデル化する元のニューラルネットワークに、推定またはコントロールしたい PDE のパラメータをモデル化するニューラルネットワークを追加したものを（一つのニューラルネットワークとして）同時に学習します。2 つのネットワークを同時に学習することで、PDE の解とパラメータを同時に求解する (= 逆問題を解く) ことが出来ます。なお、PINN を用いた逆問題の求解については別記事でより詳細に紹介する予定です。

PINN には、通常の PDE ソルバーと比較して上記のようなメリットがありますが、現時点では通常のソルバーを置き換える段階にまでは至っていません。その理由となる PINN のデメリットのうち最大のものは、failure mode [2] [3] という現象です。failure mode とは、PINN が本来求めたい PDE の解とは異なる、不適切な近似解（部分的に自明な解を含む解）を求めてしまう現象（およびその不適切な近似解そのもの）です。PINN の損失関数 $\mathcal{L}$ は、二乗誤差等の通常の教師有学習の損失関数とは異なり、初期値、境界値以外での正解値を与えていません。残りの領域ではPDE を満たすという正則化を用いて解いており、初期、境界から他の領域への情報の伝播（他の領域の関数の学習）は PDE を介して行われることになります。変化の少ない解（極端な例では自明な解など）では PDE 損失は小さな値となり、全体として見た損失も小さくなるため学習は進みません。このように、不適切な近似解をいったん学習すると、更に学習を進めても本来の解に到達出来ない事象がしばしば報告されています [4]。次節以降では、PINN の failure mode の具体例とその対策をご紹介します。

PINN の failure mode - 移流方程式を例として

本節では、前節で触れた PINN の failure mode について、具体例として移流方程式を取り上げ、どのような failure mode が生じるのか詳しくご紹介します。移流方程式は物理量が流れに沿って運ばれる過程を記述する PDE で、数式としては単純な線形 PDE ですが、数値的に解くことは決して簡単ではありません。

初期条件を正弦波とし、空間方向に周期的境界条件を課した 1 + 1 次元移流方程式は以下の数式のようになります。この PDE の厳密解は $u(t, x) = \sin (2\pi (x - \beta t))$ です。

[[ \frac{\partial u}{\partial t} + \beta \frac{\partial u}{\partial x} = 0, \\ x \in [0, 1], \; t \in [0, 2], \; \beta=8.0, \\ u(t, x=0) = u(t, x=1), \\ u(t=0, x) = \sin (2\pi x). ]]

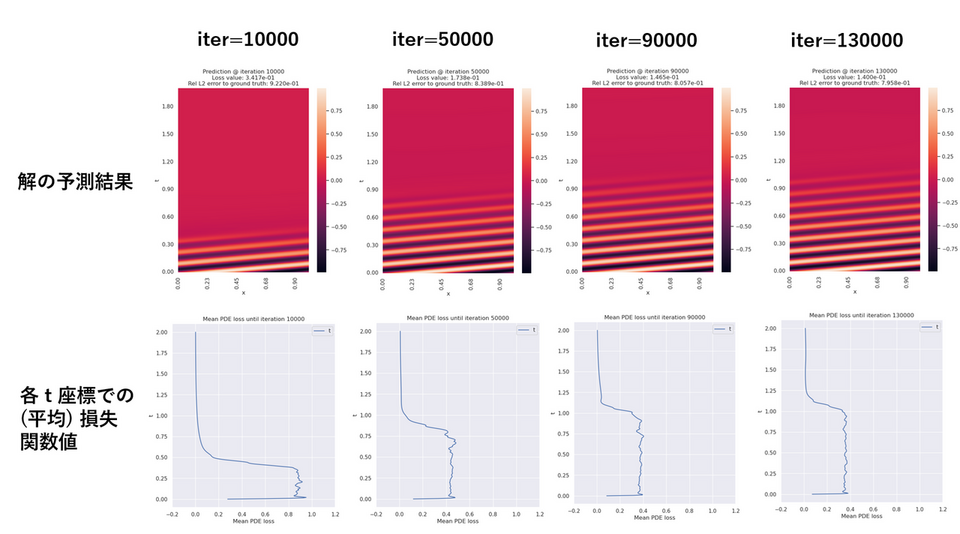
上記の移流方程式を PINN で求解した結果が Fig. 3 です。1 行目では、各 iteration での解 $u(t, x)$ の予測値をヒートマップで表示しています。学習の iteration が進むにつれて、$t=0$ での正弦波の波形が時刻 $t$ の小さい領域から大きい領域へとニューラルネットワークの学習によって伝播していく様子が確認出来ます。しかし、$t>1.0$ を超えた領域では iteration を進めても定数関数 $u(t, x) = c$ のままで正弦波が伝播していきません。これが PINN で移流方程式を学習する際の failure mode です。

なぜこのような failure mode が生じるのか考察するために、Fig.3 の 2 行目では各 $t$ 座標での PDE 損失関数の (空間) 平均値

[[ \mathcal{L}_r(t) = \frac1{N_r}\sum_{k=1}^{N_r} \biggl\lvert \frac{\partial u}{\partial t}(t, x_k) + \beta \frac{\partial u}{\partial x}(t, x_k) \biggl\rvert^2, ]]

をプロットしています。これによると、10000 iteration 未満の比較的早い段階で、 $t>1.0$ の領域での損失関数値はほとんど 0 であり、iteration を進めてもそれ以上変化しないことが分かります。実際、移流方程式 $\frac{\partial u}{\partial t} + \beta \frac{\partial u}{\partial x} = 0$ に関しては、初期条件を無視すれば、定数関数 $u(t, x) = c$ は解となっており、損失関数 $\mathcal{L}_r(t)$ についても最小値 0 となります。全領域にわたって正しい解を PINN で得るためには、$t$ の大きい領域でいったん損失関数 $\mathcal{L}_r(t)$ を増加させて定数関数解から脱出する必要があります。

言い換えると、移流方程式の failure mode では、$t=0$ の初期条件の情報が学習によって $t$ の大きい領域に伝播する前に、PINN が $t$ の大きい領域で定数関数 $u(t, x) = c$ を学習してしまい、情報の伝播がそこで妨げられる現象が起こっています。以上の観察を踏まえて、次節では PINN の failure mode を防ぐいくつかの工夫をご紹介します。

PINN の failure mode を防ぐ工夫

前節の移流方程式の例で見た通り、failure mode とは PINN の学習において情報の伝播が上手くいかず、不適切な近似解を求めてしまう現象と考えられます。こうした failure mode が大きな問題として認識されてから現在まで、 failure mode を防ぐための様々な工夫が提案されています [5]。本節では、それらの工夫をいくつかご紹介します。

まず、損失関数そのものに変更を加えて（境界での）適切な情報の伝播を陽に促す工夫として、以下の手法が提案されています。

正解値のデータを用いる：定義域内部の一部の標本点での PDE の解の正確な値が分かっている場合は、それを正解値とした二乗誤差を損失関数に加えることで、正しい PDE の解へと PINN の学習を誘導することが出来ます。
標本点の適応的重み付け：PINN の損失関数が各標本点に対する和の形になっていることに着目し、以下のように各標本点に独立に重み $\lambda_{k}$ を設定します。

[[ \mathcal{L}_r = \frac1{N_r}\sum_{k=1}^{N_r} \lambda_k \biggl\lvert \frac{\partial u}{\partial t}(t_k, x_k) + \beta \frac{\partial u}{\partial x}(t_k, x_k) \biggl\rvert^2. ]]

これらの重みを学習の過程で適切に調整することで、標本点から標本点へと情報をうまく伝播させることが出来ます。時間依存する PDE に対して、学習の初期段階では $t_k$ の小さな標本点の $\lambda_k$ が大きく、学習の進んだ段階では $t_k$ の大きな標本点の $\lambda_k$ が大きくなるように $\lambda_k$ を調整して、早い時刻の領域から遅い時刻の領域へと徐々に情報を伝播させる手法が causal PINN [6] です。また、$\lambda_k$ 自体を学習対象のパラメータとみなして、学習の過程で自動的に変化させる self-adaptive PINN (SAPINN) [7] も提案されています。

標本点リサンプリング：標本点の重みを変化させるのではなく、標本点自体を学習の過程で取りなおす手法が提案されています。R3 サンプリング [8] では、損失関数の値が小さい標本点を捨てて、新しい標本点をリサンプリングすることで、failure mode に陥らず正しい解を学習できることが確認されています。
領域分割：複雑な形状の定義域の問題では、情報を定義域全体に伝播させて正しい解を学習することが難しく、failure mode が生じる場合があります。そのような事例では、定義域を領域分割し、領域ごとにニューラルネットワークで解をモデル化する手法が提案されています [9]。

また、PINN のアーキテクチャや学習過程を工夫することで、適切な情報の伝播を陰に促す工夫として、以下の手法が提案されています。

多重スケール Fourier 特徴量ネットワーク (Multi-Scale Fourier Feature Networks, MSFFN)：ニューラルネットワークが高周波成分よりも低周波成分を先に学習してしまうスペクトルバイアスは、多重スケールの問題に対して PINN を適用した場合に情報が正しく伝播しない原因となります。ネットワークの入力となる時空座標からランダムに Fourier 特徴量を作成することで、高周波成分を学習しやすくした PINN が [10] で提案された MSFFN です。
カリキュラム学習：学習の過程をいくつかのサブタスクに分割し、それらのサブタスクを順番に学習させるカリキュラム学習も failure mode に有効であることが確認されています [2]。サブタスクの順番として、情報が正しく伝搬しやすい（簡単な）ものから学習することで、学習全体を通して情報が正しく伝播するようになります。

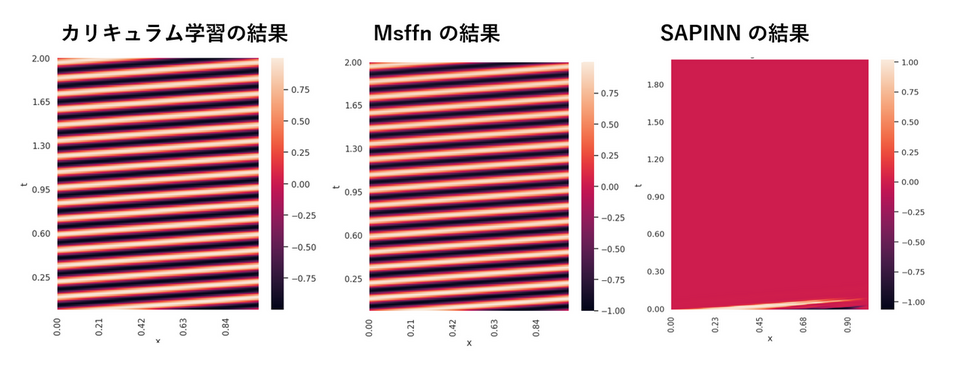
上記の手法のうちいくつかを、移流方程式の PINN に適用し failure mode を回避できるか検証した結果を以下に示します。成功例として、カリキュラム学習と MSFFN の学習結果を示すと Fig.4 (左、中) のようになり、いずれも failure mode を回避できています。なお、カリキュラム学習では移流速度 $\beta$ を徐々に大きくするカリキュラムを用いています。一方、上記の工夫の全てが移流方程式の faluire mode 回避に有効という訳ではなく、例えば、標本点の適応的重み付けのアルゴリズムである SAPINN を用いた場合はやはり failure mode が生じています (Fig.4 右)。よって、個別の問題ごとに何れの工夫が有効かを試行錯誤する事が重要になります。

Fig.4 移流方程式へのカリキュラム学習、多重スケール Fourier 特徴量ネットワーク、SAPINN の適用結果

おわりに

本記事でご紹介したように、PINN はニューラルネットワークによる新たな PDE ソルバーとして盛んに研究されています。現状では failure mode の課題があり、既存の数値計算による PDE ソルバーを置き換えるまでには至っていませんが、今後も様々な研究がなされ実用化に近づくことが期待できます。次回の記事では、PINN によるソルバーが有効と考えられている応用事例についてご紹介します。