はじめに
深層学習は画像処理や自然言語処理などのタスクで大きな成功を収めています。その理由としては、深層学習の高いモデル化能力が挙げられます(深層学習の万能近似性)。この高いモデル化能力を背景に、近年では気象学や材料科学といった科学技術分野における複雑な自然現象のモデル化にも、深層学習を適用する研究がなされるようになりました。
科学技術分野では実験や理論に基づく研究が長い間行われており、その多くは、研究対象の系が従う物理法則が判明しています。ここで、物理法則とは、Maxwell の方程式などの偏微分方程式から、エネルギー保存則や回転対称性などの系の性質などまで、広い範囲の知識を含みます。具体的な特定の物理法則に従うことが分かっている系に、深層学習などの機械学習技術を適用する際には、単にデータだけを用いるのではなく、物理法則を事前知識(prior knowledge あるいは inductive bias)として組み込むことで、効率的にモデル化することが出来ます。物理法則を事前知識として組み込み、機械学習モデルを作成する新たなアプローチを Physics-informed Machine Learning(PIML, 物理法則を組み込んだ機械学習) [1] [2] [3] とよび、近年、注目が集まっています。
物理法則を組み込んだ機械学習手法(PIML)には、純粋にデータだけを用いる手法と比較して以下のようなメリットが期待されています。
- 機械学習モデルが科学的に不合理な出力を行う可能性を減らせる。
- 教師データの量が少ない場合でも精度の良い機械学習モデルの作成が可能となる。
- 学習時に探索するモデルの空間が小さくなるため、学習にかかる時間が低減される。
- 学習時の教師データに含まれないようなデータに対する予測性能が向上する。
本記事では概説として、以下の 2 つの視点で PIML を紹介します。
- PIML が用いられる典型的な問題設定(タスク)
- PIML で物理法則を機械学習に組み込むための手法
Physics-informed Machine Learning(PIML)概説
本節では、PIML の概説として、PIML を、典型的な問題設定(タスク)、物理法則をモデルに組み込むための手法という2つの視点で紹介します。
PIML が用いられる問題設定(タスク)
PIML が用いられる典型的な問題設定(タスク)として、以下のものが挙げられます。
1. 物理システムのシミュレーション
物理システムをコンピュータ上に模倣して再現することにより、物理システムの挙動を調べることを、物理システムのシミュレーションと呼びます。物理システムのシミュレーションは、物理システムの支配方程式(量子力学のシュレーディンガー方程式や、流体のナビエストークス方程式などの偏微分方程式)が与えられている場合には、様々な条件(初期条件や境界条件)のもとで方程式を解くことで行います。一般に、これらの方程式の解析的な解が求まることはまれで、多くの場合は差分法や有限要素法といった数値解法によって近似解を求めることになります。
一方、物理システムの支配方程式が与えられていない、あるいは方程式が複雑すぎて現実的な計算資源で解けない場合には、物理システムをブラックボックスとして、データからその挙動をモデル化します。これをシステム同定と呼びます。例えば、センサを取り付けた地点の温度の観測データが手元にある場合に、それを教師データとして neural network を学習させて、領域全体における温度分布を求めることは、このようなシステム同定の具体例です。
2. 物理システムのコントロール
物理システムの支配方程式が与えられている場合には、様々な条件の元で方程式の解を求めることで、そのシステムのシミュレーションが実行できます。一方、シミュレーションとは逆に、物理システムの支配方程式とその解がデータとして与えられたもとで、そのデータを再現する条件を求める問題が物理システムのコントロールです。
また、物理システムの支配方程式が与えられていない、あるいは方程式が複雑すぎて現実的な計算資源で解けない場合にも、様々な条件下での物理システムの解のデータが存在する場合には、条件も合わせて入力データとして物理システムの挙動をモデル化することで、所望の観測結果になるような条件を求める=所望の結果になるようにシステムをコントロールする、ことができます。
システムコントロールの典型例として、指定された箱の表面の温度分布になるように箱の内部にある熱源の位置を設定する問題や、揚力比を最大化するように翼の形状を設計する問題、最適な特性を持つ材料を設計する material design/architectured materials があります。 また、方程式に現れる一部の観測可能な物理量から内部状態を推定することもシステムコントロールの典型例となります。例えば、システム生物学において、一部の化学物質の濃度の観測値から、反応速度、初期濃度などのパラメータや未観測の化学物質の濃度の時間発展を推定することや、流体の解析において、一部の観測可能な濃度の場から速度場と圧力場を推定することも行われています。
なお、物理システムのシミュレーションの事を順問題、物理システムのコントロールの事を逆問題と呼ぶ場合もあります。逆問題に関しては、リンク先の 記事 でも解説しています。
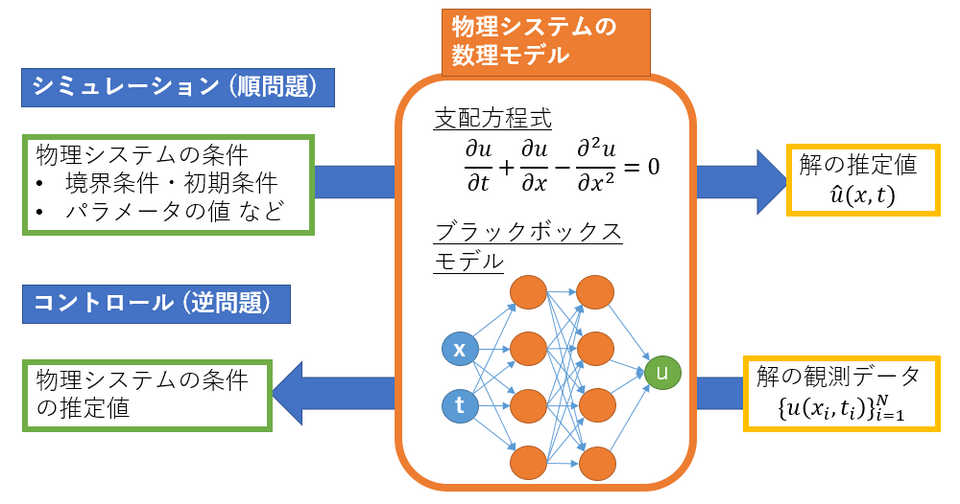 Fig.1 物理システムのシミュレーションとコントロール
Fig.1 物理システムのシミュレーションとコントロール
PIML で物理法則を組み込む手法
PIML において物理法則をモデルに組み込む主要な手法として、以下で紹介する三つがあります。
一つ目は、物理法則に従う教師データを用いてモデルを学習させるという純粋にデータドリブンなアプローチ (通常の機械学習のアプローチ)です。教師データとしては、観測や実験によって収集する場合もあれば、シミュレーションを用いてそれらをデータ拡張する場合もあります。
データドリブンなアプローチの具体例としては、物理システムのシミュレーションの項で既に上げた、限られたセンサー設置個所での温度の観測データから、 neural network で温度分布のモデルを作成するケースがあります。また、近年注目を集めるデータドリブンなアプローチの例として Neural Operator [4] [5] があります。Neural Operator は、偏微分方程式の条件 (初期条件、境界条件、外力など)を様々に変えた場合での様々な解のデータを用いて、条件 (=入力)と解(=出力)の間のマッピングを学習した neural network で、データのみから物理法則(偏微分方程式)を取り込んでいます。
二つ目は、モデルの損失関数を既知の物理法則に合わせて工夫するというアプローチです。モデルの損失関数を $\mathcal{L}$ とすると、典型的には以下の形に分解される損失関数を用いてモデルを学習させます。
[[
\mathcal{L} = \mathcal{L}_{data}(\hat{y}, y) + \mathcal{L} _{phys} (\hat{y})
]]
第一項 $\mathcal{L}_{data}(\hat{y}, y)$は、モデルの予測値 $\hat{y}$ と教師データ $y$ の間の食い違いを定量化した、通常の教師有り学習で用いられる MSE などの損失関数です。第二項 $\mathcal{L} _{phys}(\hat{y})$ は、モデルの予測値 $\hat{y}$ が物理法則を満たしている度合いを定量化した損失関数で、物理法則ごとに様々なものが考えられます。
損失関数の修正に基づくアプローチの具体例としては、Physics-informed Neural Network(PINN)[6] があります。 PINN は偏微分方程式の解の値を予測する neural network です。損失関数の $\mathcal{L}_{phys}(\hat{y})$ として予測値 $\hat{y}$ が満たすべき PDE を用いる(PDE を満たさないことに罰則を与える)ことで、深層学習モデルに偏微分方程式を組み込んでいます。
三つ目は、深層学習のネットワークアーキテクチャ自体を、既知の物理法則に合わせて工夫するというアプローチです。損失関数と同様に、組み込む物理法則毎に様々なアーキテクチャが用いられます。
特殊なアーキテクチャに基づくアプローチの具体例としては、Tensor-Basis Neural Network [7] があります。この研究では、流体のレイノルズ応力非等方テンソルを近似する neural network を作成しますが、流体現象の満たすべきガリレイ不変性を neural network の出力にも要請するために、特殊なレイヤーがアーキテクチャに導入されています。
なお、上記のアプローチを複数、組み合わせて用いる場合もあります。Hamiltonian Neural Network [8] では損失関数の修正とアーキテクチャの工夫の両方が用いられています。Physics-informed DeepOnet [9] では、データドリブンな Neural Operator に対して、偏微分方程式に基づく損失関数の修正が組み合わされています。
まとめ
ここまでで述べた、主要な PIML の手法の具体例を、問題設定(タスク)と物理法則を組み込む手法に基づいて表にすると以下のようになります。
|
物理法則を組み込む手法 |
| データドリブン |
損失関数の工夫 |
アーキテクチャの工夫 |
| 問題設定(タスク) |
物理システムのシミュレーション |
Neural Operator [4] [5] |
Physics-informed Neural Network [6] |
Tensor-Basis Neural Network [7] |
| 物理システムのコントロール |
Neural Operator [10] |
Physics-informed Neural Network [11] |
|
Physics-informed Neural Network(PINN)[6] は損失関数の修正によって偏微分方程式を neural network で求解する手法で、物理システムのシミュレーションに用いることが出来ます。Tensor-Basis Neural Network [7] は流体のレイノルズ応力非等方テンソルを近似するための neural network で、アーキテクチャに工夫をしています。Neural Operator [4] [5] は物理システム(偏微分方程式)を条件(入力)と解(出力)の間のマッピングとしてシステム同定する手法で、純粋にデータドリブンに neural network を学習させます。PINN や Neural Network を物理システムのコントロールに応用する研究 [10] [11] も提案されています。
本記事では、物理法則を組み込んだ機械学習(Physics-informed Machine Learning, PIML)について概説しました。これらはまだ発展途上の技術ではありますが、新規アルゴリズムの開発や実問題への適用が盛んに進められています。次回以降の記事では、PIML の代表的な手法の詳細を解説します。まずは、シミュレーションに対する手法として最も盛んに研究が進められている Physics-informed Neural Network(PINN)[6] について解説します。その後に Neural Operator や物理システムのコントロール(逆問題)への応用についても解説する予定です。
参考文献
雪島 正敏
株式会社NTTデータ数理システム
シミュレーション&マイニング部 部長
機械学習・シミュレーションなどの技術を活用したAI活用/データ分析の案件を年間70件以上こなすシミュレーション&マイニング部を牽引する。
常に最新技術を調査し、お客様からの様々な要件に対して最適な技術提案を行う。
清水 浩之
株式会社NTTデータ数理システム シミュレーション&マイニング部所属。
博士号(理学)取得後、当社に入社。現在は機械学習、統計解析を活用した企業や社会における課題解決に取り組んでいる。
技術調査、データ分析、モデル開発、システムへの実装といった業務を手掛ける。
趣味:旅行、歴史、美術鑑賞
