量子位相推定は、量子コンピューティングにおける最も重要なアルゴリズムの一つであり、与えられたユニタリ演算子の固有値を高精度で推定することを可能にします。
素因数分解問題を解くShorのアルゴリズム、連立一次方程式を解くHarrow-Hassidim-Lloyd (HHL) アルゴリズム、量子化学など量子計算の幅広い応用分野で使用されています。この記事では、量子位相推定の基本概念、動作原理について詳しく紹介します。
こちらは以下の記事の知識を前提としています。事前にある程度ご確認いただければ幸いです。
また量子位相推定の応用先を以下の記事にて紹介しています。
量子位相推定とは
量子位相推定 : QPE(quantum phase estimation) 、別名 Kitaevの位相推定 とは、あるユニタリ演算子 $U$とその固有状態 $\ket{\psi}$ について
[[
\begin{align*}
U\ket{\psi} = e^{i\lambda}\ket{\psi}
\end{align*}
]]
の位相(固有値) $\lambda$ を推定するアルゴリズムです。
アダマールテスト による位相推定では量子状態が収束するまで何度もサンプリングする必要がありました。位相の推定精度を$\epsilon$程度にしようと思うと、$(1/\epsilon)^2$程度のサンプリングが必要となり、高々多項式の逆数スケールでしか精度を上げられないという欠点がありました。このQPEアルゴリズムではサンプリング回数に対して指数的に精度改善できます。
アダマールテストでは1つしか用意しなかった 補助量子ビットを複数に拡張 するという手続きをとっており、1回の測定ごとに$\pm 1$の2通りの情報しか得られなかったものを、QPEでは大きな自由度に拡張することでサンプルコストを下げることが可能です。アルゴリズムの出力として、追加した補助量子ビット数分の桁数の2進小数で表現した近似位相値を、補助量子ビットの量子状態をそれぞれ1度測定することで得ることが可能です。
計算の詳細
計算手順を順々に説明していきます。
$U$の固有状態が既知の場合
まず固有値を得たいユニタリ行列$U$の固有状態が1つわかっている場合について説明します。後述しますが入力状態が固有状態の重ね合わせの場合でも全く同じ議論が使えるので、一般性は失われません。
以下の1~5が量子位相推定の計算を順に行っていく過程になります
1. $n$個の補助量子ビットの初期状態と$U$の固有状態:$U\ket{\lambda}=e^{i\lambda}\ket{\lambda}$を用意する
[[
\begin{align*}
\ket{\phi_1}=\ket{0}^{\otimes n}\ket{\lambda}
\end{align*}
]]
2. $n$個の補助量子ビットにアダマールゲートを作用させる
[[
\begin{align*}
\ket{\phi_2}=(\frac{\ket{0}+\ket{1}}{\sqrt{2}})^{\otimes n}\ket{\lambda}
\end{align*}
]]
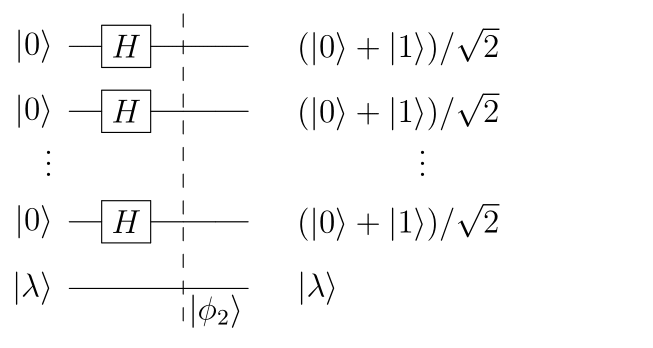 QPE:$\phi_2$まで実行した回路図
QPE:$\phi_2$まで実行した回路図
3. インデックス$k\;(k=0,...,n-1)$番目の補助量子ビットを制御、$\ket{\lambda}$を標的として$U^{2^k}$ゲートを順々に作用させる(位相キックバック)
[[
\begin{align*}
\ket{\phi_2}&=(\frac{\ket{0}+\ket{1}}{\sqrt{2}})^{\otimes n}\ket{\lambda}\\
C(U^{2^0})&\to(\frac{\ket{0}+e^{i\lambda}\ket{1}}{\sqrt{2}})(\frac{\ket{0}+\ket{1}}{\sqrt{2}})^{\otimes n-1}\ket{\lambda}\nonumber\\
C(U^{2^1})&\to(\frac{\ket{0}+e^{i\lambda}\ket{1}}{\sqrt{2}})(\frac{\ket{0}+e^{i2\lambda}\ket{1}}{\sqrt{2}})(\frac{\ket{0}+\ket{1}}{\sqrt{2}})^{\otimes n-2}\ket{\lambda}\nonumber\\
...\nonumber\\
C(U^{2^{n-1}})&\to\prod_{k=0}^{n-1}(\frac{\ket{0}+e^{i2^k\lambda}\ket{1}}{\sqrt{2}})\ket{\lambda}
\end{align*}
]]
ここで$\lambda=2\pi0.j_1j_2,...,j_n$と、小数点以下$n$桁の2進小数で近似すると以下のように表されます:
[[
\begin{align*}
\ket{\phi_3}&=\prod_{k=0}^{n-1}(\frac{\ket{0}+e^{i2^k\lambda}\ket{1}}{\sqrt{2}})\ket{\lambda}\\
&=\left(\frac{\ket{0}+e^{i2\pi0.j_1j_2...j_n}\ket{1}}{\sqrt{2}}\right)\otimes...\otimes
\left(\frac{\ket{0}+e^{i2\pi0.j_n}\ket{1}}{\sqrt{2}}\right)\ket{\lambda}
\end{align*}
]]
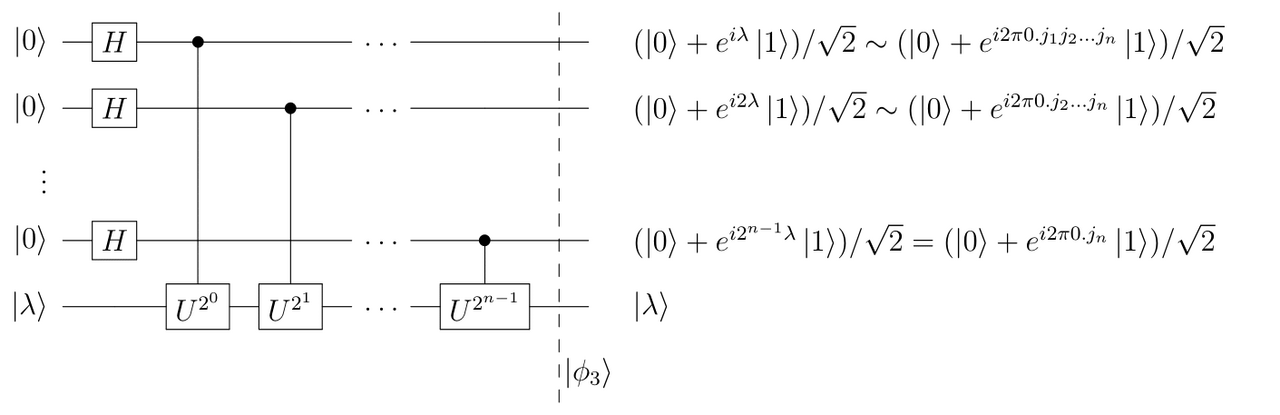 QPE:$\phi_3$まで実行した回路図
QPE:$\phi_3$まで実行した回路図
4. 補助量子ビットに逆量子フーリエ変換を行う
$\ket{\phi_3}$の補助量子ビット部の状態は状態$\ket{j_1,...,j_n}$に対して、”SWAPゲートで位相の順序を反転させない”量子フーリエ変換が行われた形となっています。
[[
\begin{align*}
&U_{{\rm QFT}}\ket{j_1,...,j_n}\\
=& \left(\frac{\ket{0}+e^{i2\pi0.j_1j_2...j_n}\ket{1}}{\sqrt{2}}\right)
\otimes...\otimes
\left(\frac{\ket{0}+e^{i2\pi0.j_n}\ket{1}}{\sqrt{2}}\right)
\end{align*}
]]
従って補助量子ビットに対し量子フーリエ変換の回路を逆向きに実行し、逆量子フーリエ変換 を行うことで、以下のように位相の情報を補助量子ビットの量子状態に書き込むことができます。
[[
\begin{align*}
&U_{{\rm QFT}}^\dagger\left(\frac{\ket{0}+e^{i2\pi0.j_1j_2...j_n}\ket{1}}{\sqrt{2}}\right)\otimes...\otimes
\left(\frac{\ket{0}+e^{i2\pi0.j_n}\ket{1}}{\sqrt{2}}\right)\ket{\lambda}\\
=& \ket{j_1,...,j_n}\ket{\lambda}
\end{align*}
]]
逆量子フーリエ変換後の状態$\ket{\phi_4}$は以下のようになります。
[[
\begin{align*}
\ket{\phi_4}
=\ket{j_1,...,j_n}\ket{\lambda}
\end{align*}
]]
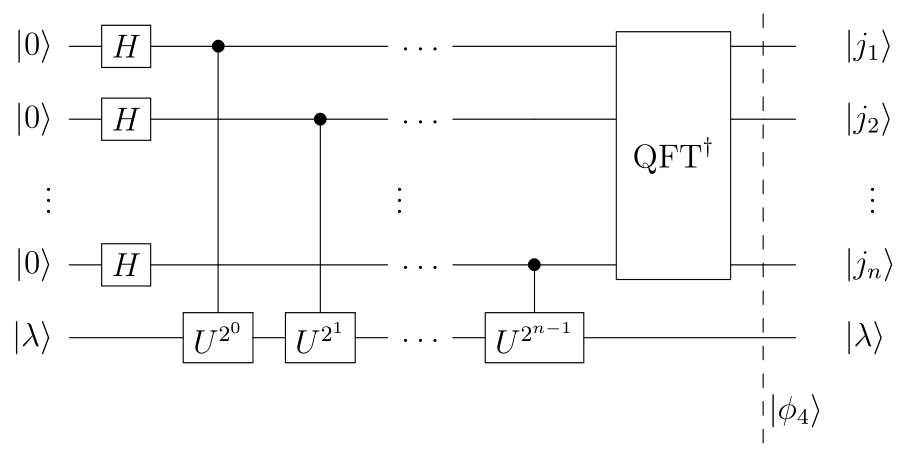 QPE:$\phi_4$まで実行した回路図
QPE:$\phi_4$まで実行した回路図
5. 補助量子ビットを測定する
$\ket{\phi_4}$から補助量子ビットを測定してそれぞれ $j_1,\dots j_n$ が確率 1 で観測できるので、$U$ の $\ket{\lambda}$ に対する固有値を $e^{i\lambda} \simeq e^{2\pi i 0.j_1\dots j_n}$ の精度で推定することができます。
このような手続きで量子位相推定は
[[
\begin{align*}
U_{{\rm QPE}}\ket{00...0}\ket{\lambda}=\ket{j_1,...,j_n}\ket{\lambda}
\end{align*}
]]
と、$U$を固有状態$\ket{\lambda}$に作用させた際の位相情報を補助量子ビットの量子状態に埋め込むことで効率的に取り出すことができるアルゴリズムとなっています。
$U$の固有状態が既知でない場合
では入力の$\ket{\lambda}$が固有状態でなく、適当な状態$\ket{\psi}$である場合を考えます。状態$\ket{\psi}$は$U$の固有状態${\ket{\lambda^{(i)}}}$で展開できるので
[[
\begin{align*}
U_{{\rm QPE}}\ket{0...0}\ket{\psi}&=U_{{\rm QPE}}\ket{0...0}(\sum_iC_i\ket{\lambda^{(i)}})\\
&=\sum_iC_i\ket{j_1^{(i)}...j_n^{(i)}}\ket{\lambda^{(i)}}
\end{align*}
]]
となり、補助系を測定すると確率$|C_i|^2$で$j_1^{(i)}...j_n^{(i)}$が得られ、入力の状態$\ket{\psi}$はユニタリ演算$U$の固有状態$\ket{\lambda^{(i)}}$と射影されます( 射影測定 )。
計算量
QPEアルゴリズムの計算オーダーを説明します。
1. 準備ステップ
補助量子ビットに$H$ゲートを作用させ、重ね合わせ状態にするステップは、各補助量子ビットで同時実行可能なため深さ1で、$\mathcal{O}(1)$の操作を必要とします。
2. 制御ユニタリ演算の適用
制御ユニタリ演算$C(U^{2^{k-1}})(k=1,\dots n)$ を適用します。このステップの計算オーダーは、次のように評価できます:
- U を 1 回適用するコストを$\mathcal{O}(C_U)$とします
- $C(U^{2^{k-1}})$を適用するコストは、最大で$\mathcal{O}(2^{k-1}C_U)$です
従って、このステップの合計コストは最大で$\mathcal{O}(2^nC_U)$となります。
3. 逆量子フーリエ変換
逆量子フーリエ変換の計算量は量子フーリエ変換と同じく $\mathcal{O}(n^2)$です:こちらの記事を参照
4. 測定
最後に、補助量子ビットを測定するステップは $\mathcal{O}(n)$の操作で実行できます。
従って、計算量は$C(U^{2^{k-1}})$を効率的に用意できるかどうかに大きく依存します。QPEが効力を発揮するのは $U^{2^{k-1}}$ が予め効率的に計算できる場合です。たとえばユニタリ演算子の一つとして回転演算子の場合、$U$ が角度 $\alpha$ の回転なら $U^{2^{k-1}}$ は $2^{k-1}\alpha$ の回転となり、$U$ ゲートの部分を $O(n^2)$ とできます。これにより合計の計算量も $\mathcal{O}(n^2)$ とできます。
終わりに
量子位相推定(QPE)は、量子コンピューティングの中核を成すアルゴリズムの一つであり、量子コンピュータの強力な計算能力を実証するための重要なツールで、ユニタリ演算の固有ベクトルが与えられたとき、それに付随する固有値を推定する方法として使用されます。本記事では、QPEの基本的な仕組み、手順について詳しく解説しました。今後、Shorのアルゴリズム(素因数分解)やHHLアルゴリズム(連立一次方程式解法)といった他の量子アルゴリズムとの関連性を理解することで、QPEの有用性とその応用範囲の広さを実感していただけると思います。
