量子アルゴリズム　～Shorのアルゴリズム～

量子位相推定の手続きを用いると様々な興味深い問題を解くことができます。ここではそのうちの1つである 量子素因数分解 、所謂 Shorのアルゴリズム について解説します。素因数分解はRSA公開鍵暗号の"カギ"となっており、それを高速に解くアルゴリズムは社会的に大きなインパクトを持つため、Shorのアルゴリズムは量子コンピューティングの研究動向が注目される大きな要因の1つとなっています。
こちらは以下の記事の知識を前提としています。事前にある程度ご確認いただければ幸いです。　

• ゲート型量子コンピュータの基礎
• 量子アルゴリズム　～アダマールテスト～
• 量子アルゴリズム　～量子フーリエ変換～
• 量子アルゴリズム　～量子位相推定～

Shorのアルゴリズムとは

Shorのアルゴリズム(Shor's algorithm) は 素因数分解問題 を解くことができるアルゴリズムですが、実際にはそれと等価な 位数発見問題 と呼ばれる問題を解くことになります。
正の整数$N$を素因数分解したいとします。$N$と共通の因数を持たない(互いに素な)正の整数を$x\; (2 \leqq x < N )$とすると、「$N$を法とする$x$の 位数 」とは、$x^r=1\;({\rm mod}\;N)$なる最小の$r$として定義されます。

位数$r$が求まるとなぜ素因数分解ができるのでしょうか。
まず$r$が偶数の場合 、$x^r=1\;({\rm mod}\;N)\to(x^{r/2}+1)(x^{r/2}-1)=0\;({\rm mod}\;N)$と式変形できます。これはつまり、

• $x^{r/2}\pm1$両方が$N$の倍数、もしくは片方が倍数で片方はNと互いに素
• $x^{r/2}\pm1$のどちらかが$N$と非自明な公約数($N$の因数)を持つ

のどちらかとなります。前者の場合は$x$の選び直しになりますが、後者になる確率の方が十分高いことが知られており、$N$と$x^{r/2}\pm1$の最大公約数のどちらかが$1,N$のどちらでもなければそれが$N$の因数ということになるわけです。最大公約数はユークリッド互除法で高速に調べることができます。従って、位数発見問題を再帰的に解いて因数を探すことで素因数分解を実行することができるわけです。

上記の位数発見問題を含むShorのアルゴリズム(因数の発見処理部分)は以下のフローチャートのようになります。

計算の詳細

整数$N$を素因数分解したいとします。計算手順を順々に説明していきます。以下の1～6が計算を順に行っていく過程になります。

1. $N$の素数判定＋比較的自明な因数の判定

このステップは基本的なShorのアルゴリズムには含まれませんが、まず与えられた整数$N$がそもそも因数を持つのかの判定を行います。$N$が素数であればアルゴリズムの再帰的に実行している部分は終了となります。
また自明な因数として、例えば$N$が偶数であれば$2$を返します。他に比較的簡単にわかる因数として、整数$\alpha\geqq 1$と$\beta\geqq2$に対して$N=\alpha^{\beta}$なる$\alpha,\beta$があれば素因数として$\alpha$を返します。

ここでは紹介は省きますが、$N$の素数判定や$N=a^b$の判定は多項式時間で解ける、効率的な古典アルゴリズムが存在します。計算コストの高い因数分解を行う前に、上記の様なある程度簡単にできる前処理は行っておくべきです。

2. $N$と互いに素な整数$x(x=0,1,...,N-1\;{\rm where}\;N=2^n)$を選んでくる

ランダムに$x$を取ってきて、ユークリッドの互除法で$N$と$x$の最大公約数を計算し、それが1以外の整数であれば$N$の非自明な約数が見つかったことになるため因数$x$を返します。一方、最大公約数が1ならば$x$は$N$と互いに素な整数であることになります。

3. $x^r=1({\rm mod}\;N)$となるような最小の整数$r$、すなわち位数を見つける(位数発見問題)

このステップを量子計算にて解くことになります。まず$\ket{y}$を$\ket{x・y\;{\rm mod}\;N}$へと移す以下のようなユニタリ演算$U_x$を定義：

[[ \begin{align} U_x=\sum_y\ket{x・y\;{\rm mod}\;N}\bra{y} \end{align} ]]

ここで$y$は$0\sim N-1$の整数で$\ket{y}$は整数基底とします。また、$U_x$は$N,x$が互いに素であることからユニタリであるといえます。
例：$x=5,N=6$

[[ \begin{align} U_x&=\ket{0}\bra{0}+\ket{5}\bra{1}+\ket{4}\bra{2}+\ket{3}\bra{3}+\ket{2}\bra{4}+\ket{1}\bra{5}\\ U_xU_x^\dagger&=\ket{0}\bra{0}+\ket{1}\bra{1}+\ket{2}\bra{2}+\ket{3}\bra{3}+\ket{4}\bra{4}+\ket{5}\bra{5}=I \end{align} ]]

$U_x$の固有状態$\ket{u_s}$と固有値は以下のように書けます(証明は付録に記載)

[[ \begin{align} \ket{u_s}=\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\exp(-\frac{i2\pi sk}{r})\ket{x^k\;{\rm mod}\;N}\;\;where\;\;(0\leqq s\leqq r-1) \end{align} ]]

また固有値は以下のように書けます：

[[ \begin{align} U_x\ket{u_s}=\exp(\frac{i2\pi s}{r})\ket{u_s} \end{align} ]]

このように$U_x$の固有値には位相$s/r$が含まれており、$r$は求めていた位数です。量子位相推定 により

[[ \begin{align} U_{{\rm QPE}}\ket{0...0}\ket{u_s} ＝\ket{j_1...j_n}\ket{u_s}\\ \end{align} ]]

となって$s/r$が求まります。ただしここで$U_x\ket{u_s}=e^{i2\pi s/r}\ket{u_s}=e^{2\pi i 0.j_1\dots j_n}$としました。 しかし、この位相推定は入力に固有状態$\ket{u_s}$を持ってこれた場合に可能な計算であり、ここに不明な$s/r$が含まれている以上は用意することができません。 そこで固有状態$\ket{u_s}$をすべて重ね合わせたものを考えます。これは

[[ \begin{align} \frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\ket{u_s}&= \frac{1}{r}\sum_{s=0}^{r-1}\sum_{k=0}^{r-1}\exp(-\frac{i2\pi sk}{r})\ket{x^k\;{\rm mod}\;N}\\ &=\frac{1}{r}\sum_{s=0}^{r-1}\ket{x^0\;{\rm mod}\;N} +\frac{1}{r}\sum_{s=0}^{r-1}\sum_{k=1}^{r-1}\exp(-\frac{i2\pi sk}{r})\ket{x^k\;{\rm mod}\;N}\\ &=\ket{1}+0=\ket{1} \end{align} ]]

となります。最後の式は右辺$\sum_{s=0}^{r-1}\exp(-\frac{i2\pi sk}{r})$が$2\pi/r$の速度でちょうど$k$回転する位相を足し合わせた和になるため対称性($r$が偶数なので反対向きの位相がある)より０となります。また$\ket{1}$は２進数表現における整数($\ket{1}=\ket{00....01}$)なことに注意してください。 以上より、$\ket{u_s}$の代わりに$\ket{1}=\frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\ket{u_s}$を入力とすることで、いずれかの$\ket{u_s}$に状態が確定し、測定結果から$s/r$を知ることができます。

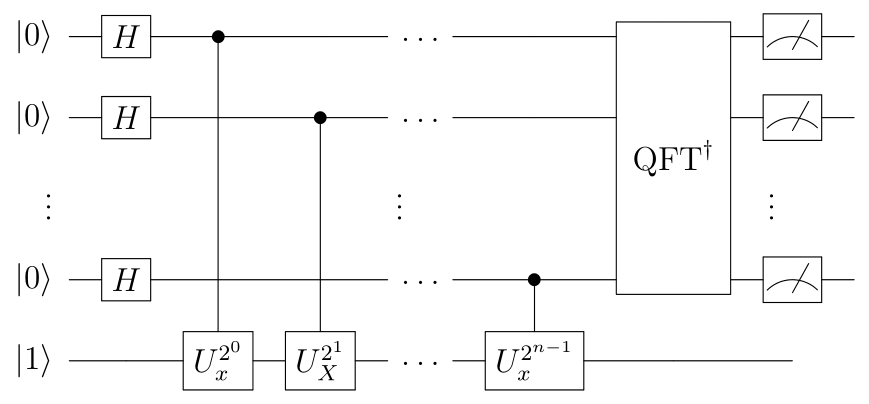
4. $s/r$は"小数の状態"で得られため、$s,r$を分離するために分数の形(最小の$r$が知りたいので約分され切った形)にする

これは 連分数展開 によって求まります(付録参照)。$r$が偶数であった場合は次のステップに進み、奇数であったならステップ２で$x$を選ぶところからやり直します。

5. $r$から$N$の因数を得る

前述の方法で$r$が偶数の場合$N$の因数を割り出します。$r$もしくは$x^{r/2}\pm1$両方が$N$の倍数、もしくは片方が倍数で片方はNと互いに素、な場合はステップ２に戻ります。

6. $N$を得られた因数で割って分割し、因数、割られた数それぞれにアルゴリズムを再帰的に適用する

具体例

分解したい数を $N = 15$とします。

1. $N$の素数判定＋比較的自明な因数の判定

Nは素数ではありません。また、比較的自明な因数の判定はここではスキップします。

2. $N$と互いに素な整数$x(x=0,1,...,N-1\;{\rm where}\;N=2^n)$を選んでくる

ここではまず$x=2$とします。$\gcd(x,N)$ を計算します。もし $\gcd(x, N) \neq 1$ なら、その $\gcd$が$N$の素因数です。$\gcd⁡(2,15)=1$なので先に進みます。

3. $x^r=1(\mod N)$となるような最小の整数$r$、すなわち位数を見つける(位数発見問題)

量子コンピュータを使って$r\;(s/r)$を求めます。ここでは$r=4$が見つかるとします($2^4=16=1\;{\rm mod}\;15$)。 量子コンピュータからは$3/4$の近似値$0.76$が得られたとして先に進みます。

4. $s/r$は "小数の状態"で得られるため、$s,r$を分離するために分数の形にする

$0.76$を連分数展開します。

[[ \begin{align} 0.76&=0+0.76\nonumber\\ &=0+\frac{1}{1+0.315789...}\nonumber\\ &=0+\frac{1}{1+\frac{1}{3+0.1666666...}}\nonumber\\ &=0+\frac{1}{1+\frac{1}{3+1/6}} \end{align} ]]

したがって、$0.76$の連分数展開は$[0;1,3,6]$です。次に連分数展開を元に$0.76$の近似分数を求めます。

• 1 : 最初の項だけを取る：$0$
• 2 : 次の項まで取る：$0+\frac{1}{1}=1$
• 3 : 次の項まで取る：$0+\frac{1}{1+1/3}=\frac{3}{4}$
• 4 : 次の項まで取る：$0+\frac{1}{1+\frac{1}{3+1/6}}=\frac{19}{25}=0.76$

今回は4項目でちょうど収束しましたが、実際にはうまく収束しないことが多いので、後述する収束判定を設けることになります。 これらの近似値のうち、最初の分数$\frac{3}{4}$の分母$4$を位数$r$候補として先に進みます。もしこれが正しくなければ、次の近似値を試していきます。

5. $r$から$N$の因数を得る

$r=4$は偶数なので$N$の因数を割り出します。

[[ \begin{align} \gcd(x-1,N)&=\gcd(4-1,15)=3\nonumber\\ \gcd(x+1,N)&=\gcd(4+1,15)=5 \end{align} ]]

これにより、$15$ の素因数として $3$ と $5$ が得られます。

6. $N$を得られた因数で割って分割し、因数、割られた数それぞれにアルゴリズムを再帰的に適用する

これ以上因数はないため終了します。

計算量

アルゴリズム中の量子位相推定(QPE)の計算量について、$U_x^{2^{n-1}}$のように指数オーダーのゲート演算を行うと、それに伴う計算コストがかかるのでは、という点が気になりますが(量子位相推定の計算量について)、今回用いる、 $x$を量子状態の$y$に乗算し、結果をモジュロ$N$で取るユニタリ演算$U_x$はうまくできており、

[[ \begin{align} U_x^{2^{k}}\ket{y} &=U_x^{2^{k}-1}\ket{xy\;{\rm mod}\;N}=U_x^{2^{k}-1}\ket{xy-C_1N}\nonumber\\ &=U_x^{2^{k}-2}\ket{x^2y-C_1Nx\;{\rm mod}\;N}=U_x^{2^{k}-2}\ket{x^2y\;{\rm mod}\;N}=U_x^{2^{k}-2}\ket{x^2y-C_2N}\nonumber\\ &=U_x^{2^{k}-3}\ket{x^3y-C_2Nx\;{\rm mod}\;N}=U_x^{2^{k}-3}\ket{x^3y\;{\rm mod}\;N}=U_x^{2^{k}-2}\ket{x^3y-C_3N}\nonumber\\ &...\nonumber\\ &=\ket{x^{2^k}y\;{\rm mod}\;N}=U_{x^{2^k}}\ket{y} \end{align} ]]

と変換できるので、事前に$U_{x^{2^k}}$を計算しておけば単体の制御ユニタリ演算は 多項式オーダーのゲート演算 で済んでしまいます。具体的にこの操作は任意の$k$について$N=2^n$として$\mathcal{O}(n^2)$で実行でき、この操作を$k=0,...,n-1$の$n$回行うためQPEは$\mathcal{O}(n^3)$で実行できます。さらに有効な位数を十分高い確率で得るための繰り返し回数により$\log n$因子が追加され、位数発見における量子位相推定の計算量は、多項式オーダーの$\mathcal{O}(n^3\log n)$となります。また、高速乗算を用いると$U_x^{2^{k}}\ket{y}$の計算量が$\mathcal{O}(n^2)$から$\mathcal{O}(n\log n\log\log n)$まで下げられ、位相推定の計算量は$\mathcal{O}(n^2(\log n)^2\log\log n)$まで下げられることが知られています。
さらに$s/r$から$r$を分離するための連分数展開は古典アルゴリズムで$\mathcal{O}(n^3)$ステップが必要になります。最後に、因数を得るために$\gcd(x\pm1,N)$をユークリッドのアルゴリズムで計算しますが、これにも$\mathcal{O}(n^3)$ステップが必要になります。もし$r$が奇数であったり、偶数であっても$\gcd(x\pm1,N)$が$1$であった場合は最初からやり直すことになります。しかし、有効な因数が得られる良いケースは高々定数回の繰り返しで得られることが知られています。以上より、Shorのアルゴリズム全体の計算量は$\mathcal{O}(n^3)$で多項式時間となります。

一方、古典的素因数分解アルゴリズムでは一般数体篩法(すうたいふるいほう)が最速で、計算量は$\mathcal{O}(e^{(64/9)^{1/3}(logN)^{1/3}(loglogN)^{2/3}})$ です。これは準指数時間であり、多項式時間で実行可能なShorのアルゴリズムと比べて大規模な数に対しては実行が困難です。

終わりに

Shorのアルゴリズムは、量子コンピューティングの中でも特に注目されるアルゴリズムであり、その実用化は計算科学のパラダイムシフトを象徴しています。本記事では、Shorのアルゴリズムの基本的な原理、手順、そしてその計算量が古典的なアルゴリズムと比較してどれほど優れているかについて詳しく解説しました。特に、量子位相推定との関係性を理解することで、Shorのアルゴリズムがどのようにして大規模な整数の素因数分解を効率的に行うのか、そのメカニズムを理解していただけたかと思います。

付録

$U_x$の固有状態と固有値の証明

$y=x^k \mod N$とは $y=x^k-CN\land$$ y < N $と書けるので($C$は適当な整数)、

[[ \begin{align} U_x\ket{x^k\;{\rm mod}\;N}=U_x\ket{x^k-CN} =\ket{x^{k+1}-CNx\;{\rm mod}\;N} =\ket{x^{k+1}\;{\rm mod}\;N} \end{align} ]]

となる。よって以下の通り：

[[ \begin{align} U_x\ket{u_s} &=U_x\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\exp(-\frac{i2\pi sk}{r})\ket{x^k\;{\rm mod}\;N}\nonumber\\ &=\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\exp(-\frac{i2\pi sk}{r})\ket{x^{k+1}\;{\rm mod}\;N}\nonumber\\ &=\frac{1}{\sqrt{r}}\sum_{k'=1}^{r}\exp(-\frac{i2\pi s(k'-1)}{r})\ket{x^{k'}\;{\rm mod}\;N}\nonumber\\ &=\exp(\frac{i2\pi s}{r})\frac{1}{\sqrt{r}}\sum_{k'=1}^{r}\exp(-\frac{i2\pi sk'}{r})\ket{x^{k'}\;{\rm mod}\;N}\nonumber\\ &=\exp(\frac{i2\pi s}{r})\frac{1}{\sqrt{r}}[\sum_{k'=1}^{r-1}\exp(-\frac{i2\pi sk'}{r})\ket{x^{k'}\;{\rm mod}\;N}+\exp(-i2\pi s)\ket{x^0\;{\rm mod}\;N}]\;\;(x^r\;{\rm mod}\;N=x^0\;{\rm mod}\;N=1より)\nonumber\\ &=\exp(\frac{i2\pi s}{r})\frac{1}{\sqrt{r}}\sum_{k'=0}^{r-1}\exp(-\frac{i2\pi sk'}{r})\ket{x^{k'}\;{\rm mod}\;N}\nonumber\\ &=\exp(\frac{i2\pi s}{r})\ket{u_s} \end{align} ]]

以上より$U_x$の固有状態・固有値は以下の通り：

[[ \begin{align} \ket{u_s}&=\frac{1}{\sqrt{r}}\sum_{k=0}^{r-1}\exp(-\frac{i2\pi sk}{r})\ket{x^k\;{\rm mod}\;N}\\ U_x\ket{u_s}&=\exp(\frac{i2\pi s}{r})\ket{u_s} \end{align} ]]

連分数展開

小数$y$に最も近似された分数を推定するには連分数展開を行います。連分数展開とはある実数$z$を整数$a_n$を用いて以下のように展開することです。

[[ \begin{align} z=a_0+\frac{1}{a_1+\frac{1}{a_2+\frac{1}{...}}} \end{align} ]]

ここで$a_n\;(n=0,1,...)$は

• $a_0=\lfloor z\rfloor,\;b_0=\frac{1}{z-a_0}$
• $a_n=\lfloor b_{n-1}\rfloor,\;b_n=\frac{1}{b_{n-1}-a_n}$

と整数部分との分離、小数部分の反転を繰り返すアルゴリズムを用いて機械的に計算することができます。$z$が有理数であれば展開は有限の項数で終わります。連分数展開後、$z$の分数近似形は

[[ \begin{align} z\sim\frac{c_n}{d_n} \end{align} ]]

と求めることができます。ここで、$c_0=a_0,c_1=1+a_0a_1,c_n=a_nd_{n-1}+c_{n-2}$、$d_0=1,d_1=a_1,d_n=a_nd_{n-1}+d_{n-2}$となっています。
連分数展開には以下のような収束判定が存在します。

定理：$s/r$が$|s/r-z|\leqq 1/2r^2$を満たす有理数であるとき、$s/r$は$z$に対する連分数の収束値(近似分数)であり、さらに$s,r$の最大公約数は１である

従って、補助量子ビットの数を$2L+1$とすると、$z$は$2L+1$ビット精度なため、連分数展開が十分行われた際の$s/r$と$z$の差は以下のように抑えられます。

[[ \begin{align} |\frac{s}{r}-z|\leqq\frac{1}{2^{2L+1}} \end{align} ]]

さらに$r\leqq N\leqq2^L$より

[[ \begin{align} |\frac{s}{r}-z|\leqq\frac{1}{2^{2L+1}}\leqq\frac{1}{2r^2} \end{align} ]]

が導けます。従って、$2L+1$ビット精度で$z$を求め、上式(収束判定)が満たされるまで連分数展開を行うことで、完全に約分されてかつ最も近似された$s/r$、すなわち最小の$r$を手に入れることができます。実際に$r$が位数かどうかは$x^r\;{\rm mod}\;N=1$となるかどうかを計算することでチェックできます。
連分数展開が収束するまでに必要な演算の回数は$\mathcal{O}(L^3)$と見積もることができます。