量子アルゴリズム　～アダマールテスト～

量子計算では量子ビットに対する演算の結果を演算子（ゲート）の 固有値 や 期待値 といった情報として取得することがあります。アダマールテスト はユニタリ演算の任意の量子状態に対する期待値、固有状態に対する固有値を推定する最もシンプルな方法の一つです。

アダマールテストの発展である量子位相推定は量子素因数分解（Shorのアルゴリズム）など有名なアルゴリズムに幅広く応用されているため、アダマールテストへの理解を深めることが、より複雑な量子アルゴリズムを理解する手引きとなるはずです。この記事では、アダマールテストについての概要と計算の詳細について解説します。

こちらは以下の記事の知識を前提としています。事前にある程度ご確認いただければ幸いです。

• ゲート型量子コンピュータの基礎

量子力学の基礎

量子力学を知らない人向けに、ここでは量子力学の量子状態のブラケット記法、固有値、演算子の期待値について簡単にまとめます。これらについてよくご承知の方はこの説明は飛ばしていただいて結構です。

ブラケット記法

量子ビットの状態を表す ケット（ket） とは列ベクトルに相当するものです。例えば、1量子ビットの基底は

[[ \begin{align} \ket{0} &= \begin{pmatrix}1\\0\end{pmatrix} \nonumber \\ \ket{1} &= \begin{pmatrix}0\\1\end{pmatrix} \end{align} ]]

のように書かれ、一般の１量子ビット状態 $\ket{\psi}$ は $|\alpha|^2 + |\beta|^2 = 1$ を満たす複素数 $\alpha, \beta$ を用いて、

[[ \begin{align} \ket{\psi} = \alpha\ket{0} + \beta\ket{1} = \begin{pmatrix} \alpha \\ \beta \end{pmatrix} \end{align} ]]

と書けます。

これに対してケットの双対を ブラ（bra） といい、これは行ベクトルに相当します。ブラとケットを同じ記号で書くときは、片方はもう片方の複素転置（$\dagger$ をつけて表す）となります。例えば基底は

[[ \begin{align} \bra{0} &= (1\; 0) = \ket{0}^\dagger　\nonumber\\ \bra{1} &= (0\; 1) = \ket{1}^\dagger \end{align} ]]

となり、先ほどの $\ket{\psi}$ に対応するのは

[[ \begin{align} \bra{\psi} = \ket{\psi}^\dagger = (\alpha^* \; \beta^*) \end{align} ]]

となります。二つのベクトルの 内積 は、片方をブラ、もう片方をケットとして、これらを続けて書きます。$\ket{\phi} = \begin{pmatrix} \gamma \ \delta \end{pmatrix}$ と先ほどの $\ket{\psi}$ の内積は、

[[ \begin{align} \Braket{\psi|\phi} = (\alpha^* \; \beta^*)\begin{pmatrix} \gamma \\ \delta \end{pmatrix} = \alpha^*\gamma + \beta^* \delta \end{align} ]]

となります。二つ目の等号では行列の積を計算しています。$\ket{0}, \ket{1}$ は正規直交基底をなしており、

[[ \begin{align} \Braket{0|0} = \Braket{1|1} = 1 \nonumber\\ \Braket{1|0} = \Braket{0|1} = 0 \end{align} ]]

が成り立ちます。

演算子

演算子 という言葉は、数学や物理学で「何かを操作する道具」として使われます。例えば、普通の数学では「+」や「-」といった記号が演算子です。

量子計算における演算子とは、量子ビットに対して特定の操作を行うためのものです。これにより、量子ビットの状態を変更したり、特定の計算を実行したりします。量子計算の演算子は、（量子）ゲート と呼ばれるもので構成されています。これらのゲートは、各量子ビットに対して特定の操作を行います。

演算子（ゲート）は行列のように表現できますが、ケットとブラをこの順に組み合わせて表現することもできます。ベクトルに作用させる計算も、行列とベクトルと同様におこなえばよいです。例えば、アダマールゲートは

[[ \begin{align} H = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \end{align} ]]

ですが、$\ket{0},\ket{1}$に作用させると、

[[ \begin{align} H\ket{0}&=\frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix}1\\0\end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix}1\\1\end{pmatrix} = \frac{\ket{0}+\ket{1}}{\sqrt{2}}, \nonumber \\ H\ket{1}&=\frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix}0\\1\end{pmatrix} = \frac{1}{\sqrt{2}} \begin{pmatrix}1\\-1\end{pmatrix} = \frac{\ket{0}-\ket{1}}{\sqrt{2}} \end{align} ]]

となります。これより、基底の正規直交性を思い出すとアダマールゲートは

[[ \begin{align} H = \frac{\ket{0}+\ket{1}}{\sqrt{2}}\bra{0} + \frac{\ket{0}-\ket{1}}{\sqrt{2}}\bra{1} \end{align} ]]

と書くこともできます。

固有値

固有値 という概念は、特定の操作（演算）を行ったときにその操作の対象（例えば、量子ビット）の状態が変わらない場合に、その状態に対応する数値を指します。

ある演算子 $A$、 状態 $\ket{\psi}$、 複素数 $a$ について

[[ \begin{align} A\ket{\psi} = a\ket{\psi} \end{align} ]]

が成り立つとき、すなわち $A$ を作用させても状態は変化せず係数のみが変わるようなとき、この状態 $\ket{\psi}$ を $A$ の 固有状態（固有ベクトル） と言い、係数 $a$ を固有値と言います。たとえば、$Z$ ゲート

[[ \begin{align} Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} = \ket{0}\bra{0} - \ket{1}\bra{1} \end{align} ]]

の固有状態は $\ket{0}, \ket{1}$ で固有値は $+1, -1$ です。実際、

[[ \begin{align} Z\ket{0} &= +\ket{0} \nonumber\\ Z\ket{1} &= -\ket{1} \end{align} ]]

となって、状態は変化せず係数 $\pm 1$ のみが出ています。

アダマールテストとは

アダマールテストとは、ユニタリ行列を入力の量子状態（ベクトル）に作用させた際の 固有値や期待値を推定する アルゴリズムです。入力状態$\ket{\psi}$がユニタリ演算子$U$の固有状態のときは対応する固有値が推定でき、一般の状態が入力として与えられたときは期待値が推定できます （※量子計算における期待値については付録で解説します）。

アダマールテストの回路は以下の通りです。

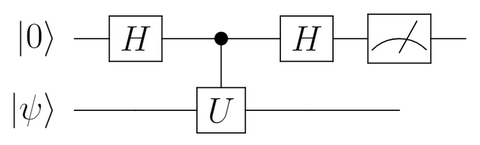
入力には $\ket{\psi}$ のほかに、補助量子ビットとして $\ket{0}$ を用います。補助ビットと制御ゲートを用いることで、$\ket{\psi}$ への $U$ の作用をうまく観測結果として取り出すことができます。$\ket{\psi}$への$U$の演算結果を直接測定するのではなく、補助量子ビットを通して間接的に測定することになります。こうした測定方法は「 間接測定 」と呼ばれます。

古典コンピュータでこの回路をシミュレートしようとすると、$\ket{\psi}$ の量子ビット数 $n$ に対して$U$の行列サイズが $2^n$ と指数的に大きくなるため、大きい $n$ に対しては現実的な時間で解くのが難しくなります。量子コンピュータでは、複雑すぎない $U$ に対してなら量子ビット数 $n$ に対して高々多項式回のサンプリングで期待値や固有値の値を十分な精度で近似することができます。

計算の詳細

ここでは入力状態$\ket{\psi}$ が $U$ のある固有状態である場合を考えます （※固有状態でない場合に関しては付録で扱います）。

ユニタリ演算の場合、固有値の絶対値は必ず1になるため、すべての固有値は$e^{2\pi i \theta}$という表示で表すことができます。この$2\pi \theta$の部分を量子ビットが持つある種の回転の自由度として 位相 と呼びます。位相が定まることで固有値が定まるため、量子計算における固有値推定は位相の推定と同義になります。ここでは位相を$\lambda$とおきます。

[[ \begin{align} U\ket{\psi}=e^{i\lambda}\ket{\psi} \end{align} ]]

以下の1～4が上記のアダマールテストの回路図の演算を左から順に行っていく過程になります。

1. 補助量子ビットにアダマールゲートを作用させる

アダマールゲート $H$ は

[[ \begin{align} H = \frac{\ket{0}+\ket{1}}{\sqrt{2}}\bra{0} + \frac{\ket{0}-\ket{1}}{\sqrt{2}}\bra{1} \end{align} ]]

ですから、一つ目のゲートを通った後の状態 $\ket{\phi_1}$ は、

[[ \begin{align} \ket{\phi_1} = H\ket{0}\otimes\ket{\psi} = \frac{\ket{0}+\ket{1}}{\sqrt{2}} \otimes \ket{\psi} \end{align} ]]

で、補助量子ビットは$\ket{0}$と$\ket{1}$の重ね合わせ状態となっています。

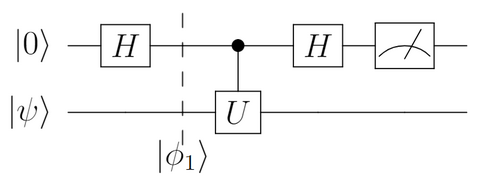
2. 制御ユニタリゲートを適用する

ユニタリ演算$U$ に対する 制御ゲート $\mathrm{C}(U)$ は、制御ビット である補助量子ビットが $\ket{0}$ なら何もせず、$\ket{1}$ なら第 2 ビットに $U$ を作用させる、というものです。制御ゲートは回路図上ではターゲットビットに作用させる演算と制御ビットの黒丸を直線でつないで表現します。これは式を表記すると以下のようになります：

[[ \begin{align} \mathrm{C}(U) = \ket{0}\bra{0}\otimes I + \ket{1}\bra{1}\otimes U \end{align} ]]

$\ket{\phi_1}$を$\mathrm{C}(U)$ ゲートに通します。量子コンピュータでは重ね合わせ状態の$\ket{0}$と$\ket{1}$にそれぞれ同時並行で演算を実行することができます。その後の状態 $\ket{\phi_2}$ は

[[ \begin{align} \ket{\phi_2} &= \mathrm{C}(U) \ket{\phi_1} \nonumber\\ & = \left(\ket{0}\bra{0}\otimes I + \ket{1}\bra{1}\otimes U\right)\left(\frac{\ket{0}+\ket{1}}{\sqrt{2}} \otimes \ket{\psi} \right) \nonumber\\ & = \frac{1}{\sqrt{2}}\ket{0}\otimes\ket{\psi} + \frac{1}{\sqrt{2}}\ket{1}\otimes U\ket{\psi} \\ \end{align} ]]

となります。ところで今は$\ket{\psi}$が$U$の固有状態であるため、

[[ \begin{align} \ket{\phi_2} & = \frac{1}{\sqrt{2}}\ket{0}\otimes\ket{\psi} + \frac{e^{i\lambda}}{\sqrt{2}}\ket{1}\otimes \ket{\psi} \nonumber\\ & = \frac{\ket{0}+e^{i\lambda}\ket{1}}{\sqrt{2}}\otimes\ket{\psi} \\ \end{align} ]]

とすることもできます。$\ket{\phi_1}$と比較すると、 $\ket{1}$ にのみ$e^{i\lambda}$ が係数として追加されている事がわかります。$\ket{0}$の係数が$e^{i0}$で位相が$0$だと思えば、$\ket{1}$との位相差が$\lambda$だけ増えたことになります。このような$\ket{0}$と$\ket{1}$の位相差を 相対位相 といいます。$\mathrm{C}(U)$を通すことで$\ket{\psi}$ の固有値の情報を補助ビットの相対位相として取り出せたことがわかります。このことを 位相キックバック といいます。

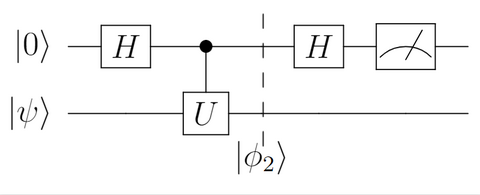
3. 補助量子ビットにアダマールゲートを作用させる（2回目）

補助量子ビットにアダマールゲートを通すと、その後の状態 $\ket{\phi_3}$ は

[[ \begin{align} \ket{\phi_3} & =\frac{1}{\sqrt{2}}H\ket{0}\otimes\ket{\psi} + \frac{1}{\sqrt{2}}H\ket{1}\otimes U\ket{\psi} \nonumber\\ & = \frac{1}{2}\left(\ket{0} + \ket{1}\right) \otimes \ket{\psi} + \frac{1}{2}\left(\ket{0}-\ket{1}\right) \otimes U\ket{\psi} \nonumber\\ & = \frac{1}{2}\ket{0}\otimes(I+U)\ket{\psi} + \frac{1}{2}\ket{1}\otimes(I-U)\ket{\psi}\\ \end{align} ]]

となります。

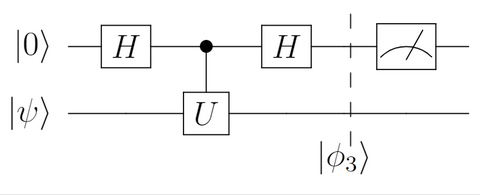
4. 測定する

最後に補助量子ビットを測定します。おさらいですが、量子ビットの状態が$\ket{\psi}=\alpha\ket{0}+\beta\ket{1}$であるとき、この量子ビットを測定して0が得られる確率は$p_0=|\alpha|^2$でした。従って、状態 $\ket{\phi_3}$ に対して 0 を観測する確率 $p_0$ は、上の$\ket{\phi_3}$ 式の最終行第１項より

[[ \begin{align} p_0 &= \left|\frac{1}{2}(I+U)\ket{\psi}\right|^2 \nonumber\\ & = \frac{1}{4} \Braket{\psi|(I+U^\dagger)(I+U)|\psi} \nonumber\\ &= \frac{1}{4}\Braket{\psi|2I+U+U^\dagger|\psi} \quad (\because U^\dagger U = I)\nonumber\\ &= \frac{2 + \Braket{\psi | U | \psi} + \Braket{\psi | U | \psi}^*}{4} \quad (\because \Braket{\psi|\psi}=1)\nonumber\\ &= \frac{1 + \operatorname{Re}\Braket{\psi | U | \psi}}{2} \end{align} ]]

となります。さらに今は$\ket{\psi}$が$U$の固有状態であるため、

[[ \begin{align} p_0 =\frac{1 + \operatorname{Re}\Braket{\psi | e^{i\lambda} | \psi}}{2} = \frac{1 + \cos\lambda}{2} \end{align} ]]

となります。補助量子ビットで 1 を観測する確率 $p_1$ も同様にして

[[ \begin{align} p_1 = \left|\frac{1}{2}(I-U)\ket{\psi}\right|^2 = \frac{1-\operatorname{Re}\Braket{\psi|e^{i\lambda}|\psi}}{2}=\frac{1 - \cos\lambda}{2} \end{align} ]]

となります。

回路に通す前後で第 2 ビットの状態 $\ket{\psi}$ は不変なので、同様の計算を十分な回数を行えば、第１ビットで0を観測した割合が$p_0$に、1を観測した割合が $p_1$ に収束し、固有値$e^{i\lambda}$の実数部である$\cos\lambda$ を十分な精度で推定することができます。また、基本的に量子状態は測定すると重ね合わせ状態が解消され、状態が変化してしまいますが、アダマールテストは$\ket{\psi}$ が不変であるままに固有値の推定ができる 間接測定 となっています。

更に固有値$e^{i\lambda}$の虚数部である$\sin\lambda$に関しては、$C(U)$を実行する前に$S^\dagger$ゲート

[[ \begin{align} S^\dagger=\ket{0}\bra{0} - i \ket{1}\bra{1}=\begin{pmatrix}1&0\\0&i\end{pmatrix} \end{align} ]]

を補助量子ビットに挿入させることによって推定できます。

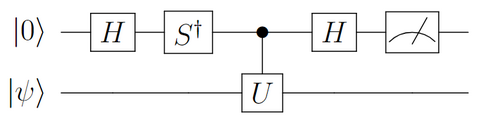
実際、$S^\dagger$ゲート後の状態 $\ket{\phi_1^\prime}$は

[[ \begin{align} \ket{\phi_1^\prime} &= S^\dagger H\ket{0}\otimes\ket{\psi} \nonumber\\ &= S^\dagger \frac{\ket{0}+\ket{1}}{\sqrt{2}} \otimes \ket{\psi} \nonumber\\ &= \frac{\ket{0}-i\ket{1}}{\sqrt{2}} \otimes \ket{\psi} \nonumber\\ &= \frac{1}{\sqrt{2}} \ket{0} \otimes \ket{\psi} - \frac{i}{\sqrt{2}} \ket{1} \otimes \ket{\psi} \end{align} ]]

となり、次の $\mathrm{C}(U)$ ゲートを通すと、そのあとの状態 $\ket{\phi_2^\prime}$ は

[[ \begin{align} \ket{\phi_2^\prime} &= \mathrm{C}(U) \ket{\phi_1^\prime} \nonumber\\ & = \left(\ket{0}\bra{0}\otimes I + \ket{1}\bra{1}\otimes U\right) \left(\frac{1}{\sqrt{2}}\ket{0}\otimes\ket{\psi} - \frac{i}{\sqrt{2}}\ket{1}\otimes\ket{\psi}\right) \nonumber\\ & = \frac{1}{\sqrt{2}}\ket{0}\otimes\ket{\psi} - \frac{i}{\sqrt{2}}\ket{1}\otimes U\ket{\psi} \\ \end{align} ]]

となり、最後にアダマールゲートを通すと、状態 $\ket{\phi_3^\prime}$ は

[[ \begin{align} \ket{\phi_3^\prime} = & \frac{1}{\sqrt{2}}H\ket{0}\otimes\ket{\psi} - \frac{i}{\sqrt{2}}H\ket{1}\otimes U\ket{\psi} \nonumber\\ & = \frac{1}{2}\left(\ket{0} + \ket{1}\right) \otimes \ket{\psi} - \frac{i}{2}\left(\ket{0}-\ket{1}\right) \otimes U\ket{\psi} \nonumber\\ & = \frac{1}{2}\ket{0}\otimes(I-iU)\ket{\psi} + \frac{1}{2}\ket{1}\otimes(I+iU)\ket{\psi}\\ \end{align} ]]

となります。よって、

[[ \begin{align} p_0 &= \left|\frac{1}{2}(I-iU)\ket{\psi}\right|^2\nonumber\\ & = \frac{1}{4} \Braket{\psi|(I+iU^\dagger)(I-iU)|\psi} \nonumber\\ &= \frac{1}{4}\Braket{\psi|2I-iU+iU^\dagger|\psi} \quad (\because U^\dagger U = I)\nonumber\\ &= \frac{2 -i\left(\Braket{\psi | U | \psi} - \Braket{\psi | U | \psi}^*\right)}{4} \nonumber\\ &= \frac{1 + \operatorname{Im}\Braket{\psi | U | \psi}}{2} \end{align} ]]

となるので、

[[ \begin{align} p_0 =\frac{1 + \operatorname{Im}\Braket{\psi | e^{i\lambda} | \psi}}{2} = \frac{1 + \sin\lambda}{2} \end{align} ]]

となります。確率 $p_1$ も同様にして

[[ \begin{align} p_1 = \left|\frac{1}{2}(I+iU)\ket{\psi}\right|^2 = \frac{1-\operatorname{Im}\Braket{\psi|e^{i\lambda}|\psi}}{2}=\frac{1 - \sin\lambda}{2} \end{align} ]]

となり、虚数部も推定する事ができます。

推定の誤差と計算量について

$N$ 回アダマールテストをおこない、そのうち $N_0$ 回で補助量子ビットに 0 を観測したとします。Hoeffding の不等式（証明は省略します）より、$\varepsilon > 0$ について

[[ \begin{align} \operatorname{Prob}\left(\left|\frac{N_0}{N}-p_0\right| \geq \varepsilon\right) \leq 2e^{-2\varepsilon^2 N} \end{align} ]]

が成り立ちます。よって、$N = O(1/\varepsilon^2)$ 回程度アダマールテストをおこなえば、上式の右辺は小さくなり、$|N_0/N - p_0|\geq \varepsilon$ となる確率も十分小さくなります。したがって $p_0$、ひいては $\cos\lambda$ を誤差 $\varepsilon$ で推定するには、$1/\varepsilon$ についての多項式オーダー $O(\operatorname{poly}(1/\varepsilon))$ のアダマールテストをおこなえばよい、ということになります。

なお、1 回のアダマールテストにかかる計算量は、$U$ や $H$ のゲートを作用させるのにかかる時間によって変わります。例えば、量子ビット数 $n$ に対して $U$ が $O(n)$, $H$ が $O(1)$ で計算できるとすると、期待値の推定は $O(n\operatorname{poly}(1/\varepsilon))$ の時間でできる、ということになります。実際にどうなるかは、$U$ がどのような演算子であるかのほかに、具体的な量子コンピュータの実装にもよります。

終わりに

この記事では量子アルゴリズムの理解への手引きとしてアダマールテストの紹介をしました。入力状態をユニタリ行列の固有状態にすればその固有値を、一般の状態とすれば期待値を推定することができます。アダマールテストでは補助ビット 1 つだけ用いて何度も回路からサンプリングすることで推定を実行しましたが、発展版の量子位相推定では補助ビットを増やすことでサンプリング回数が大幅に削減され、より実用的なアルゴリズムとなっています。

• 量子アルゴリズム　～量子位相推定～

付録 : 入力状態が $U$ の固有状態ではない場合

ここでは量子力学における期待値の概念と、アダマールテストにおいて入力状態$\ket{\psi}$が$U$の固有状態でないときの、$U$の期待値測定について解説します。

量子力学では、ある状態 $\ket{\psi}$ に対してある種の操作を実行した際の結果が確率的に定まります。つまり演算子 $A$ に対応する物理量（何かしらの値）を測定したときの結果の値も 確率的にしか定まりません 。測定値を出現確率で重みづけして全て足し合わせるとまさしく 期待値 となります。量子力学では演算子$A$の期待値は次のように表されます。

[[ \begin{align} \Braket{A}=\Braket{\psi|A|\psi} \end{align} ]]

実際にこれが期待値となっているのか、以下に詳しく見ていきます。

例えば、状態$\ket{\psi}$を以下のように定義します。

[[ \begin{align} \ket{\psi}=\sum_iq_i\ket{a_i} \end{align} ]]

ここで$\ket{a_i}$は完全直交基底で$A\ket{a_i}=a_i\ket{a_i}$を満たすような演算子$A$の固有状態とします。測定によって状態$\ket{a_i}$を得る確率$p_i$は係数の絶対値２乗である$p_i=|q_i|^2$と紹介していましたが、これは量子力学における次のような確率の定義から得られています。

[[ \begin{align} p_i=\left| \Braket{a_i|\psi} \right|^2 \end{align} ]]

実際に、

[[ \begin{align} p_i=\left| \bra{a_i}\sum_jq_j\ket{a_j} \right|^2=|q_i|^2 \end{align} ]]

と係数の絶対値２乗と一致していることがわかります。これは 射影測定 と呼ばれる測定の結果で、射影演算子

[[ \begin{align} \rho_i=\ket{a_i}\bra{a_i} \end{align} ]]

を作用させ、その結果の期待値を取っていることに相当します。この射影演算子は

[[ \begin{align} \rho_i\ket{\psi}=q_i\ket{a_i} \end{align} ]]

といったように重ね合わせ状態を１つの状態に収束（つまり射影）させてしまいます。つまり、射影測定によって状態$\ket{a_i}$が得られることが確認できた後は、すでに状態が１つに収束してしまっているため、何度測定しても$\ket{a_i}$が得られることになります。射影演算子の期待値は

[[ \begin{align} \Braket{\psi|\rho_i|\psi}=\sum_jq_j^*\Braket{a_j|a_i}\bra{a_i}\sum_kq_k\ket{a_k}=q_i^*q_i=|q_i|^2 \end{align} ]]

となって、$\ket{a_i}$が得られる確率$p_i$と一致している事がわかります。実際の操作としては$\ket{\psi}$を何度も射影測定し、$\ket{a_i}$が得られたときを1、その他の状態が得られたときを0としてその期待値（つまり割合）を取っていくと、この値に収束することになります。

演算子$A$はこの射影演算子を用いて以下のように定義することができます。

[[ \begin{align} A=\sum_ia_i\rho_i=\sum_ia_i\ket{a_i}\bra{a_i} \end{align} ]]

これは状態$\ket{\psi}$を射影測定し、状態が$\ket{a_i}$に収束した場合は値として固有値$a_i$が得られる演算子とも解釈できます。$\bra{\psi}A\ket{\psi}$を実際に計算すると確かに古典的な期待値と一致していることも確認できます。

[[ \begin{align} \Braket{A}&=\bra{\psi}A\ket{\psi}\nonumber\\ &=\sum_jq_j^*\bra{a_j}\left(\sum_ia_i\ket{a_i}\bra{a_i}\right)\sum_kq_k\ket{a_k}\nonumber\\ &=\sum_ia_i|q_i|^2\nonumber\\ &=\sum_ia_ip_i \end{align} ]]

ただし実際の操作として、$\ket{\psi}$に演算子$A$を作用させて基底$\ket{a_i}$の下で射影測定を行っても得られるのはそれぞれの状態$\ket{a_i}$のみで、何度も測定することでその出現割合である$p_i$はわかりますが、依然として固有値$a_i$はわからないため期待値$\Braket{A}$を得ることはできません。

アダマールテストではこの期待値の値を補助ビットの射影測定の確率値として取り出せるようになっています。

固有値推定のときと同様の回路で、式$(20)$より、

[[ \begin{align} p_0 = \frac{1 + \operatorname{Re}\Braket{\psi | U | \psi}}{2} \end{align} ]]

となるので補助ビットが0となる確率$p_0$から期待値の実部 $\operatorname{Re}\Braket{\psi | U | \psi}$ が推定できます。

$S^\dagger$ゲートを差し込んだ場合、式$(27)$より

[[ \begin{align} p_0 = \frac{1 + \operatorname{Im}\Braket{\psi | U | \psi}}{2} \end{align} ]]

となるので確率$p_0$から期待値の虚部 $\operatorname{Im}\Braket{\psi | U | \psi}$ を推定できます。