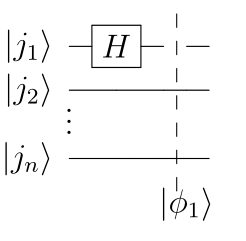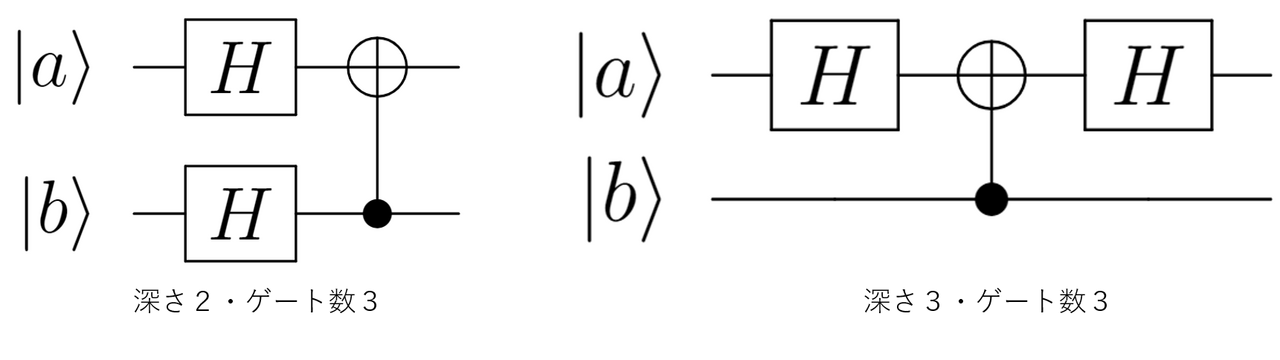量子コンピュータでは社会的に重要な問題を、従来のコンピュータよりも遥かに高速に解くことができます。
この記事ではショアのアルゴリズム(量子素因数分解)やその他多くの量子アルゴリズムにおける重要な構成要素である 量子フーリエ変換 について、その概要と計算の詳細について解説します。
こちらは以下の記事の知識を前提としています。事前にある程度ご確認いただければ幸いです。
また量子フーリエ変換の応用先を以下の記事にて紹介予定です。
離散フーリエ変換とは
量子フーリエ変換の説明の前に、比較対象として挙げられる古典的な 離散フーリエ変換(DFT : discrete Fourier transform) についての紹介をしておきます。
DFTは$N$個の標本点$x(=0,1,...,N-1)$に対して値(波形)が関数$f(x)$にて与えられているとき、$f(x)$を以下のような関数$F(y)$へと移す変換です。
[[
\begin{align}
F(y)=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}f(x)e^{2\pi ixy/N}
\end{align}
]]
ここで$y$は波数であり、$F(y)$の振る舞いを確認することで、$f(x)$を周期性で分解した際の支配的な成分を確認することに役立ちます。一般的なフーリエ変換との違いは、有限な周期を持つ離散的な関数に対して適応可能な点です。DFTは高速フーリエ変換(FFT)という手法で$\mathcal{O}(N\log N)$の計算量で計算することができます。
量子フーリエ変換とは
量子フーリエ変換 : QFT(quantum Fourier transform) は、$x,y$を整数列$0,1,2,...,N-1\;\;(N=2^n)$とし、対応する量子状態を$\ket{x},\ket{y}$としたとき、以下のようなユニタリ演算で記述されます:
[[
\begin{align}
U_{{\rm QFT}}=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}\sum_{y=0}^{N-1}e^{2\pi ixy/N}\ket{x}\bra{y}
\end{align}
]]
そして$\ket{y}$に対して以下のような変換を行います:
[[
\begin{align}
U_{{\rm QFT}}\ket{y}=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}e^{2\pi ixy/N}\ket{x}
\end{align}
]]
古典のDFTの式と見比べると対応関係が見えると思います。またここで、状態$\ket{x},\ket{y}$は整数$x,y$を2進数表示とした場合の
[[
\begin{align}
x&=i_12^{n-1}+i_22^{n-2}+...+i_n2^0 \nonumber\\
y&=j_12^{n-1}+j_22^{n-2}+...+j_n2^0
\end{align}
]]
に対応する量子状態 $\ket{x}=\ket{i_1,...,i_n},\ket{y}=\ket{j_1,...,j_n}$としています(例えば$\ket{1}=\ket{00,...,01}$,$\ket{2}=\ket{00,...,10}$のようになる)。
QFTはフーリエ変換の文脈で解釈すると 入力状態を位相の周期性に変換 することに相当しています。例えば$n$量子ビットにて$y=2$を入力とするとこれに対する$\ket{x}$の位相(係数)は$e^{2\pi ix・2/N}$となります。これはすなわち$x$が$0\to N-1$と変化する間に$x=0,N/2$の2回、位相が1になるため周期は2となるわけです。
このようにQFTを通して量子状態$\ket{y}$に書き込まれている整数情報 $y$ が位相部分に書き込まれる事になります。一方その 逆変換は位相の情報を量子状態に書き込む ことに使用されます。こういった操作が量子位相推定などの他の量子アルゴリズムで用いられています。
実際の量子回路上での変換を確認するため、$\ket{x},\ket{y}$に2進数を代入してQFTの変換式をみることにします。式$(3)$に代入:
[[
\begin{align}
\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}e^{2\pi ixy/N}\ket{x}
&=\frac{1}{\sqrt{2^n}}\sum_{i_1=0}^1...\sum_{i_n=0}^1\exp(2\pi i(i_12^{n-1}+...+i_n2^0)y/2^n)\ket{i_1,...i_n}\nonumber\\
&=\frac{1}{\sqrt{2^n}}\sum_{i_1=0}^1...\sum_{i_n=0}^1\exp(2\pi i(i_12^{-1}+...+i_n2^{-n})y)\ket{i_1,...i_n}\nonumber\\
&=\left(\frac{1}{\sqrt{2}}\sum_{i_i=0}^1e^{i2\pi i_12^{-1}y}\ket{i_1}\right)\otimes...\otimes\left(\frac{1}{\sqrt{2}}\sum_{i_n=0}^1e^{i2\pi i_n2^{-n}y}\ket{i_n}\right)\nonumber\\
&=\left(\frac{\ket{0}+e^{i2\pi2^{-1}y}\ket{1}}{\sqrt{2}}\right)\otimes...\otimes\left(\frac{\ket{0}+e^{i2\pi2^{-n}y}\ket{1}}{\sqrt{2}}\right)
\end{align}
]]
ここで$y=j_12^{n-1}+j_22^{n-1}+...+j_n2^0$を代入しますが、位相の $2\pi・$整数 部は$2^{i2\pi・整数}=1$になるため無視してよく、以下のようになります。
[[
\begin{align}
\left(\frac{\ket{0}+e^{i2\pi(2^{-1}j_n)}\ket{1}}{\sqrt{2}}\right)\otimes...\otimes
\left(\frac{\ket{0}+e^{i2\pi(2^{-1}j_1+...+2^{-n}j_n)}\ket{1}}{\sqrt{2}}\right)
\end{align}
]]
さらに位相は 二進小数表示 ($0.j_1...j_n=\frac{j_1}{2}+...+\frac{j_n}{2^n}$)として以下のようにも書けます。
[[
\begin{align}
\left(\frac{\ket{0}+e^{i2\pi0.j_n}\ket{1}}{\sqrt{2}}\right)\otimes...\otimes
\left(\frac{\ket{0}+e^{i2\pi0.j_1j_2...j_n}\ket{1}}{\sqrt{2}}\right)
\end{align}
]]
つまりQFTは2進数表示にて以下のような変換になっており、最終的にこの形を目指して回路を組んでいくことになります。
[[
\begin{align}
U_{{\rm QFT}}\ket{j_1,...,j_n}=\left(\frac{\ket{0}+e^{i2\pi0.j_n}\ket{1}}{\sqrt{2}}\right)\otimes...\otimes
\left(\frac{\ket{0}+e^{i2\pi0.j_1j_2...j_n}\ket{1}}{\sqrt{2}}\right)
\end{align}
]]
 QFTの回路図
QFTの回路図
計算の詳細
以下の1~5が上記のQFTの回路図の演算を左から順に行っていく過程になります
1. $n$量子ビット状態$\ket{y}=\ket{j_1,...,j_n}$の1番目の量子ビット$\ket{j_1}$にアダマールゲートをかける
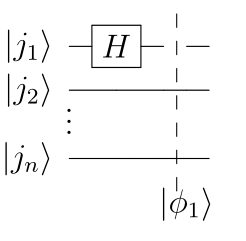 QFT : $\phi_1$ まで
QFT : $\phi_1$ まで
アダマールゲートの作用は以下のようでした:
[[
\begin{align}
H\ket{0} = \frac{\ket{0}+\ket{1}}{\sqrt{2}}\nonumber\\
H\ket{1} = \frac{\ket{0}-\ket{1}}{\sqrt{2}}
\end{align}
]]
これは$j_1=0\; {\rm or}\;1$に対して以下のように1つの式にまとめることができます:
[[
\begin{align}
H\ket{j_1}=\frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.j_1}\ket{1})
\end{align}
]]
ここで2進数表示なので$0.1=1/2$であることに注意してください。状態は以下のようになります:
[[
\begin{align}
\ket{\phi_1} =\frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.j_1}\ket{1})\ket{j_2...j_n}
\end{align}
]]
2. $\ket{j_2}$を制御ビットとして1番目の量子ビットに回転ゲート : $R_z(2\pi/2^2)$をかける
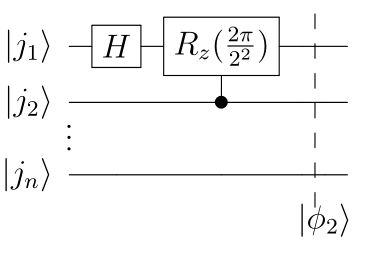 QFT : $\phi_2$ まで
QFT : $\phi_2$ まで
回転ゲート$R_z$ の行列表現は以下のようになります:
[[
\begin{align}
R_z(\theta)=\begin{bmatrix}e^{-i\theta/2} & 0 \\ 0 & e^{i\theta/2}\end{bmatrix}=e^{-i\theta/2}\begin{bmatrix}1 & 0 \\ 0 & e^{i\theta}\end{bmatrix}
\end{align}
]]
これは$\ket{0},\ket{1}$に$\theta$の位相差を追加する効果であり、基本的に$\ket{1}$側の位相を$\theta$増やす効果として扱います。今は$\ket{j_2}$を制御ビットとして1番目の量子ビットに$R_z(2\pi/2^2)$を作用させているため、$\ket{j_2}$が1の時のみ1番の量子ビットの$\ket{1}$に$2\pi/2^2$だけの位相が追加されます。そこで1番の量子ビットの$\ket{1}$に$2\pi j_2/2^2$の位相を追加すれば、$j_2=1$のときのみ$2\pi/2^2$の位相を追加するのと同じ扱いになるため、状態$\ket{\phi_2}$は以下のようになります:
[[
\begin{align}
\ket{\phi_2} =\frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi j_2/2^2}e^{i2\pi0.j_1}\ket{1})\ket{j_2,...,j_n}
\end{align}
]]
さらに2進数表示で$1/2^2=0.01$を用いて状態は以下のようも書けます:
[[
\begin{align}
\ket{\phi_2} &=\frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.0j_2}e^{i2\pi0.j_1}\ket{1})\ket{j_2,...,j_n} \nonumber\\
&=\frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.j_1j_2}\ket{1})\ket{j_2,...,j_n}
\end{align}
]]
3. 同様に3番目以降の量子ビット$\ket{j_k}$を制御ビットとして1番目の量子ビットに$R_z(2\pi/2^k)$をかけていく
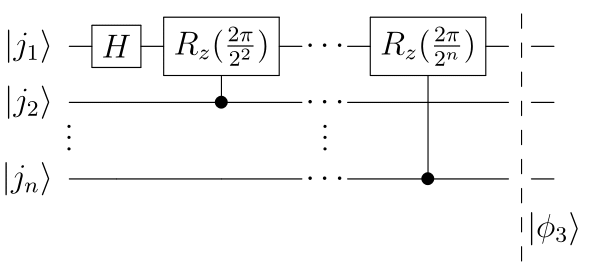 QFT : $\phi_3$ まで
QFT : $\phi_3$ まで
[[
\begin{align}
\ket{\phi_3}=\frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.j_1...j_n}\ket{1})\ket{j_2,...,j_n}
\end{align}
]]
4. 2番目以降の量子ビット$\ket{j_k}$に関しても1~3と同様にアダマールゲートをかけて$k'=k+1\sim n$までの$R_z(2\pi/2^{k'-k+1})$を作用させていく
 QFT : $\phi_4$ まで
QFT : $\phi_4$ まで
[[
\begin{align}
\ket{\phi_4}=\frac{\ket{0}+e^{i2\pi0.j_1...j_n}\ket{1}}{\sqrt{2}}\otimes\frac{\ket{0}+e^{i2\pi0.j_2...j_n}\ket{1}}{\sqrt{2}}\otimes...\otimes\frac{\ket{0}+e^{i2\pi0.j_n}\ket{1}}{\sqrt{2}}
\end{align}
]]
このままでは各量子ビットの状態の順序が目的の式$(8)$と逆なため、反転させる必要があります。
5. SWAPゲートで量子ビットを入れ替え、順序を反転させる
 QFT : $\phi_5$ まで
QFT : $\phi_5$ まで
SWAPゲート は2つの量子ビットを交換する($\ket{01}\to\ket{10}$)ゲート演算で、行列表現は以下のようになります:
[[
\begin{align}
U_{{\rm SWAP}} = \begin{pmatrix}1&0&0&0\\0&0&1&0& \\ 0&1&0&0\\0&0&0&1\end{pmatrix}
\end{align}
]]
きちんと位相も入れ替わっていることが分かります
[[
\begin{align}
U_{{\rm SWAP}}(\alpha\ket{0}+\beta\ket{1})(\alpha'\ket{0}+\beta'\ket{1})&=U_{{\rm SWAP}}(\alpha\alpha'\ket{00}+\beta\alpha'\ket{10}+\alpha\beta'\ket{01}+\beta\beta'\ket{11})\nonumber\\
&=\alpha\alpha'\ket{00}+\beta\alpha'\ket{01}+\alpha\beta'\ket{10}+\beta\beta'\ket{11}\nonumber\\
&=(\alpha'\ket{0}+\beta'\ket{1})(\alpha\ket{0}+\beta\ket{1})
\end{align}
]]
回路上ではSWAPゲートは以下のように3つのCNOTゲートで作成することができます。
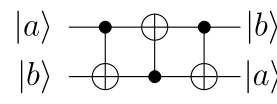 SWAP
SWAP
上記の回路により$\ket{ab}$は4パターンそれぞれで以下のように変化し、確かにSWAPゲートが構成できていることが分かります。
- $\ket{00}\to\ket{00}\to\ket{00}\to\ket{00}$
- $\ket{10}\to\ket{11}\to\ket{01}\to\ket{01}$
- $\ket{01}\to\ket{01}\to\ket{11}\to\ket{10}$
- $\ket{11}\to\ket{10}\to\ket{10}\to\ket{11}$
SWAPゲートを$(\ket{j_1},\ket{j_n}),(\ket{j_2},\ket{j_{n-1}})...$と順序反転させるように各ペアに作用させていき、目的としていた状態を得ることができます。
[[
\begin{align}
\ket{\phi_5}=\left(\frac{\ket{0}+e^{i2\pi0.j_n}\ket{1}}{\sqrt{2}}\right)\otimes...\otimes
\left(\frac{\ket{0}+e^{i2\pi0.j_1j_2...j_n}\ket{1}}{\sqrt{2}}\right)
\end{align}
]]
回路中に出てくるゲート演算は全てユニタリーなため、QFTもユニタリーとなっています。そのため逆変換は上記の回路を逆に向きに進めることに相当します。
計算量について
量子アルゴリズムは、量子ゲートのシーケンスとして表現されます。つまり、ある計算を実行するためには、その計算を実現するために必要な量子ゲートの配列を特定します。量子アルゴリズムの計算時間は、最も長いゲート操作の連鎖、すなわち量子回路の深さ(ステップ数)に依存します。
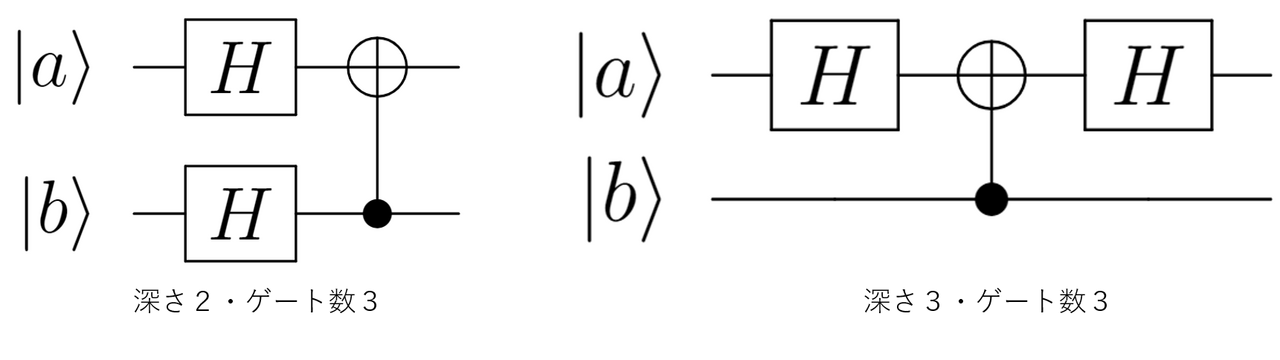
一方、古典計算では、計算の複雑さは典型的にはアルゴリズムのステップ数や実行する命令の数で評価されます。例えば、ソートアルゴリズムでは、比較操作や交換操作の数が重要な評価基準となります。
ではQFT回路は何回のゲート演算を必要とするでしょうか。SWAPゲートを抜きにすると、
- 1番目の量子ビット:1回のアダマールゲートと$n-1$回の条件付きゲート
- 2番目の量子ビット:1回のアダマールゲートと$n-2$回の条件付きゲート
- ...
- $n$番目の量子ビット:1回のアダマールゲートと$1$回の条件付きゲート
となり、合わせると$n+(n-1)+...+1=n(n-1)/2$だけのゲートが必要なことが分かります。SWAPゲートはペアの数である$n/2$回、3つのCNOTゲートを作用させればよいので$3n/2$ゲートとなります。従ってこの回路では$\mathcal{O}(n^2)$のゲート演算でQFTを実行できます。
一方、標本数が$N(=2^n)$個のDFTを古典アルゴリズムで実行する場合、最良のアルゴリズムである高速フーリエ変換(FFT)を用いても$\mathcal{O}(N\log N)\sim\mathcal{O}(2^nn)$回の演算が必要なことが分かっています。つまり、QFTは古典のフーリエ変換よりも 指数的に高速 であると言えます。
では今後、音声などのデジタル化された古典データをフーリエ変換する際、QFTがFFTの代わりに用いられるようになっていくでしょうか。これは実は難しく、現在古典フーリエ変換をQFTに置き換える効率的な方法は知られていません。これは終状態の回路からフーリエ係数を読み出すのに 指数的な回数の反復測定 を行う必要があるためです。
終わりに
今回の記事では量子フーリエ変換の紹介をしました。量子フーリエ変換単体では指数関数的な高速化を得るのは難しいですが、以降に紹介する量子位相推定や、ショアのアルゴリズムではこれを巧妙に利用し、量子の強みを活かした高速なアルゴリズムを構成しています。