- HOME
- 量子計算による最適化アルゴリズム~QAOA~
量子近似最適化アルゴリズム(Quantum Approximate Optimization Algorithm: QAOA)は、量子アニーリング(QA)に着想を得てゲートベースの量子コンピュータを活用して最適化問題の解を求めるために設計された量子アルゴリズムです。従来のコンピュータでは計算に膨大な時間がかかる問題に対し、QAOAはQAと同様に量子力学の特性を利用してより効率的に解を提供する可能性があります。
位相推定やショアのアルゴリズムといった代表的な量子アルゴリズムを行うには、大規模な量子回路を実装できる量子コンピュータの開発を待たなくてはならず、数十年先までかかると言われています。
一方、QAOAは現在開発されている小~中規模の量子コンピュータに実装することが可能です。小~中規模でかつ(誤り訂正ができないため)計算途中でノイズが乗ってしまうような量子コンピュータを NISQ(Noisy Intermediate-Scale Quantum) デバイスといい、QAOAはNISQデバイスでも実行可能な NISQアルゴリズム と言われています。
QAOAは、金融分野でのポートフォリオ最適化や物流分野での配送経路の最適化など、さまざまな実世界の問題に応用研究がなされています。これらの分野では、QAOAを用いることで、従来の手法よりも効率的に高品質な解を得られる可能性が示されています。近年の量子コンピュータの発展とともに、QAOAは今後さらに多くの分野での応用が期待されており、量子計算の実用化に向けた重要なステップとされています。
本記事では以下の内容を扱います。
1. QAOAの紹介
2. QAOAの実行手順
3. QAOAを発展させたアルゴリズムであるQAOA+の紹介
4. 量子計算シミュレータのQiskitを用いたQAOA・QAOA+によるポートフォリオ最適化のシミュレーション
こちらは以下の記事の知識を前提としています。事前にある程度ご確認いただければ幸いです。
QAOAとは
量子アニーリングについて
QAOA は 量子アニーリング(Quantum Annealing : QA) から着想を得て設計された量子アルゴリズムです。そこでQAの仕組みから順を追って解説していくことにします。前提知識として量子アニーリングの解説をご参照いただければより理解しやすいと思います。
QAは、物理現象に基づく最適化手法で、イジングモデルや量子ビットを利用して最適解に相当する基底状態(最小エネルギー状態)を探索します。QAは以下のようなハミルトニアン$H(t)$の時間依存進化を利用します。
[[ \begin{align} H(t)=(1-s(t))H_M+s(t)H_P \end{align} ]]
ここで、$H_M$は計算初期の量子揺らぎによる無秩序な状態を生成する「 ミキサーハミルトニアン 」で、横磁場を表すパウリ$X$行列などが用いられます。$H_P$は最適化問題を表現する「 問題ハミルトニアン 」で、エルミート行列の形で表されます。$s(t)$は時間変化のスケジュールを決める関数で、時刻$t$ ともに 0 から 1 へと変化し、これによりハミルトニアンが徐々に$H_M$から$H_P$へと変化します。
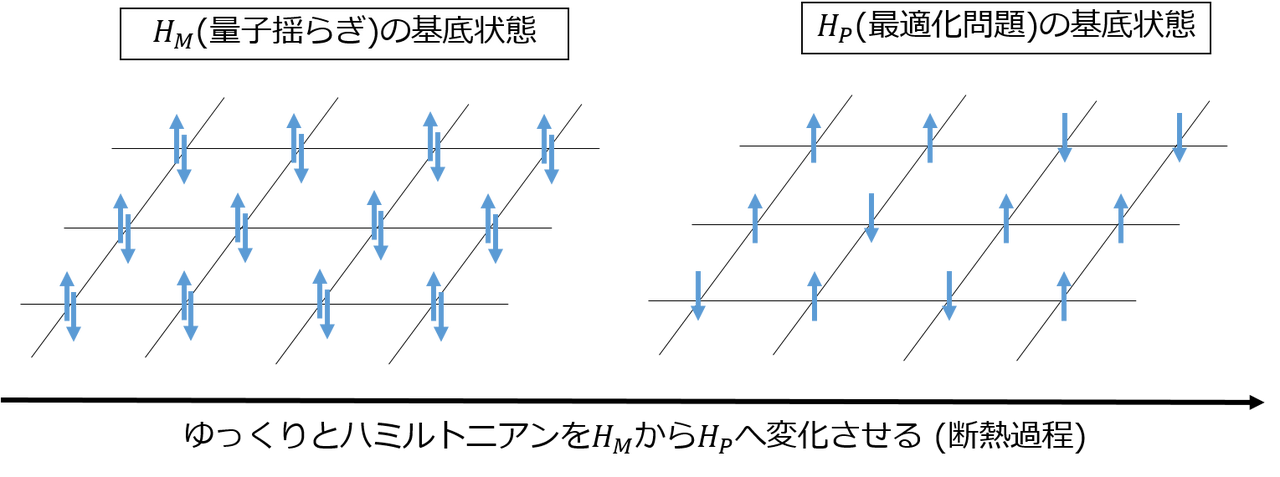
このプロセスの最終目標は、問題ハミルトニアン$H_P$の基底状態に到達することで、QAを成功させるには、初期状態として$H_M$の基底状態を用意し、システムが断熱条件、つまり常に基底状態に留まるようにゆっくりと変化することを条件としています。
時間発展の離散化
QAOAはQAのアナログなプロセスをゲート型量子コンピュータ用に 離散化 つまりデジタル化して適用した近似アルゴリズムです。
物理学・量子力学に馴染みのない方からすると少しむずかしいかもしれませんが、あるハミルトニアン$H(t)$における量子状態$\ket{\psi(t)}$の時間発展(時刻による状態の変化)は次のような シュレディンガー方程式 によって記述されます。
[[ \begin{align} i\hbar\frac{\partial}{\partial t}\ket{\psi(t)}=H(t)\ket{\psi(t)} \end{align} ]]
$\hbar$はディラック定数と呼ばれ、量子力学に現れるスケール定数です。このハミルトニアン$H(t)$における時刻$0$から$t_f$への時間発展の結果は以下のように記述されます。
[[ \begin{align} U\ket{\psi(0)}=\ket{\psi(t_f)},\;\;U=\exp\left(-\frac{i}{\hbar}\int_0^{t_f}H(t)dt\right) \end{align} ]]
$U$は時間発展演算子と呼ばれ、ここではまさしく状態$\ket{\psi(0)}$から状態$\ket{\psi(t_f)}$への時間変化を表現しています。この時間発展は時刻$t$に関する連続な積分が入ってしまっているため、デジタルなゲート式量子コンピュータでは表現しきれません。そこで積分の離散化を行うにあたり、時刻$t\sim t+\delta t$のごく短い時間では$H(t)$は変化しないとしてしまいます。その結果$U$は以下のように近似されます。
[[ \begin{align} U&\sim\exp\left(-\frac{i}{\hbar}(H(0)\delta t+H(\delta t)\delta t+...+H(t_f-\delta t)\delta t+H(t_f)\delta t)\right) \nonumber\\ &=\prod_{t=0}^{t_f}\exp\left(-\frac{i}{\hbar}H(t)\delta t\right) \end{align} ]]
つまり、$\exp\left(-\frac{i}{\hbar}H(t)\delta t\right)$という演算を$t$を少しずつ変えながら離散的に量子状態に対してかけていけば良いことになります。ところでエルミート行列$A$の指数行列$e^{A}$はユニタリ行列となることが知られており、ゲート式量子コンピュータの量子ゲートとしての必要条件であるユニタリ性を満たしています。しかし、$H(t)$はエルミート演算子$H_M$と$H_P$の和で構成されており、この2つは基本的には非可換な行列で、その和の指数行列はユニタリ行列になりません。つまりこのままではゲート式量子コンピュータの量子ゲートとして実装することができません。
そこで 鈴木=トロッター分解 と呼ばれる近似を利用します。鈴木=トロッター分解では非可換な行列$A,B$の和の指数行列をそれぞれの指数行列の積に分解します。
[[ \begin{align} e^{\delta(A+B)}=e^{\delta A}e^{\delta B}+\mathcal{O}(\delta^2) \end{align} ]]
これを$U$に当てはめると以下のようになります。
[[ \begin{align} U\sim\prod_{t=0}^{t_f}\exp\left(-\frac{i}{\hbar}(1-s(t))H_M\delta t\right)\exp\left(-\frac{i}{\hbar}s(t)H_P\delta t\right) \end{align} ]]
これでユニタリ演算を順々にかけることで量子回路上でも$U$を表現できるようになりました。さらに$\hbar$はスケールのための定数なので$1$としてしまい、時間の分割数を整数$i=1,...,p$として明確にパラメートライズすると$U$は以下のように表現できます。
[[ \begin{align} U&=\prod_{i=1}^{p}\exp\left(-i\beta_iH_M\right)\exp\left(-i\gamma_iH_P\right)\nonumber\\ &=\prod_{i=1}^{p}U_M(\beta_i)U_P(\gamma_i)\\ \beta_i&=(1-s(t))\delta t = (1-s(t_f\frac{i-1}{p-1}))\frac{1}{p}\\ \gamma_i&=s(t)\delta t =s(\frac{i-1}{p-1})\frac{1}{p} \end{align} ]]
以上より、式$(6)$に従って、$U_M(\beta_i),U_P(\gamma_i)$を初期状態$\ket{\psi(0)}$に順次作用させて行くことがシュレディンガー方程式の時間発展に相当し、時間発展の終状態$\ket{\psi(t_f)}$を得ることができます。初期状態$\ket{\psi(0)}$はQAに習って$H_M$の基底状態とします。例えば$H_M$にパウリ$X$を選択した場合は$\ket{0}$に$H$ゲートを作用させた$\ket{+}$を初期状態とします。
量子回路のパラメータとチューニング
QAでは断熱定理といって、ハミルトニアンを$H_M$から$H_P$に非常にゆっくり変化させると状態が最適解にたどり着くことが保証されています。その場合は時間変化のスケジュールを決める$s(t)$に計算の結果は左右されません。しかし現実に行われる計算は、デバイスの問題で量子性を長くは保てないために、非常に短時間で計算を行う必要があり、その場合はスケジュール$s(t)$が解の精度に影響してきます。
QAOAでは離散分割数$p$をなるべく大きく取ることがQAにおける断熱時間発展に相当し、パラメータ${\beta_1,...,\beta_p,\gamma_1,...,\gamma_p}$がスケジュール$s(t)$に相当します。$p$を大きく取ることはそれだけ量子回路が大規模化することを意味するため、NISQデバイスのような小~中規模の量子コンピュータでは$p$の大きさを制限するしかなく、解の精度を上げるには適切なパラメータ${\beta_1,...,\beta_p,\gamma_1,...,\gamma_p}$をチューニングする必要があります。
パラメータチューニングを行う際、その目的関数として終状態$\ket{\psi(t_f)}$を代入した$H_P$の値を用いることになりますが、測定される$\ket{\psi(t_f)}$は確率的にばらつくため、1度の測定結果から$H_P$の値を算出するのではなく、何度かサンプリングを行った上での期待値$\Braket{\psi(t_f)|H_P|\psi(t_f)}$を目的関数として最小化します。チューニング自体は古典コンピュータ上で行われ、更新されたパラメータを用いて再度量子回路を構成して逐次更新していきます。
終状態$\ket{\psi(t_f)}$はパラメータ${\beta_1,...,\beta_p,\gamma_1,...,\gamma_p}$でパラメートライズされており、それを明示して$\ket{\psi(t_f)}=\ket{\beta_p\gamma_p}$のように記述します。$\ket{\beta_p\gamma_p}$のようなパラメートライズされた量子状態(波動関数)やそれを生成するパラメートライズされた量子回路のことを ansatz(試行波動関数) と呼びます。
実行手順
ゲート方量子コンピュータ回路上でのQAOAの実行手順について説明していきます。
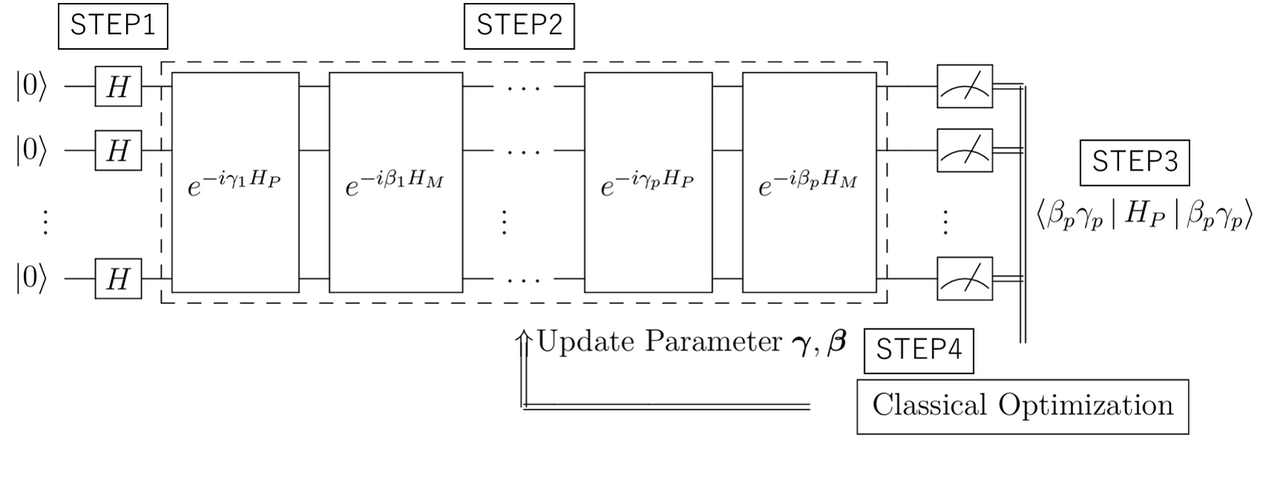
問題ハミルトニアン$H_P$は$n$ qubitで表される最適化問題とします。
1. 初期状態を作成する
基本的には$H_M$としてQAと同様にパウリ$X$を選択し、初期状態はパウリ$X$の固有ベクトルであり、基底状態でもある$\ket{+}=\frac{\ket{0}+\ket{1}}{\sqrt{2}}$の$n$ qubit重ね合わせ状態である$|s⟩=\ket{+}^{\otimes n}$を初期状態とします。この状態は$\ket{0}$にアダマールゲートを適用することで作れます。
2. ユニタリ演算を順次適用する
パラメータ$\beta_i,\gamma_i$に応じて状態に$U_M(\beta_i)=\exp\left(-i\beta_iH_M\right),U_P(\gamma_i)=\exp\left(-i\gamma_iH_P\right)$を順次作用させていき、終状態$\ket{\beta_p,\gamma_p}$を得ます。
3. エネルギー期待値を推定する
期待値$\Braket{\beta_p\gamma_p|H_P|\beta_p,\gamma_p}$を推定します。期待値測定の方法は代表的なものとしてアダマールテストなどがありますが、非効率なため、以下のような手法が用いられます。
ハミルトニアン$H_P$はエルミート行列であり、任意のエルミート行列は単位行列・パウリ行列の直積と線形結合で表現されます。そこで$H_P$を構成している要素を取り出して、$\Braket{\beta_p\gamma_p|Z|\beta_p,\gamma_p}$や$\Braket{\beta_p\gamma_p|ZX|\beta_p,\gamma_p}$のように分解したそれぞれの要素の期待値をサンプリング結果から推定し、それらを足し合わせて$H_P$を再構成することで期待値$\Braket{\beta_p\gamma_p|H_P|\beta_p,\gamma_p}$を推定します。
基本的にゲート型量子コンピュータではパウリ$Z$基底での測定しか想定していないため、パウリ$X,Y$にあたる箇所を測定する際は事前に回転ゲートを作用させてパウリ$Z$に揃えます(回転ゲートはベクトルの長さ(すなわち確率の大きさ)は変えないため、作用させても結果は変わりません)。
また、複数量子ビットにまたがる$Z_1Z_2$のような演算子の期待値を測定する場合は、状態を$\ket{\psi}=a_{00}\ket{00}+a_{01}\ket{01}+a_{10}\ket{10}+a_{11}\ket{11}$とすると期待値は
[[ \begin{align} \Braket{\psi|Z_1Z_2|\psi}=|a_{00}|^2-|a_{01}|^2-|a_{10}|+|a_{11}|^2 \end{align} ]]
となり、$|a_{00}|^2+|a_{11}|=1が偶数個出た確率,|a_{01}|^2+|a_{10}|=1が奇数個出た確率$なため、
[[ \begin{align} \Braket{\psi|Z_1Z_2|\psi}=1が偶数個出た確率-1が奇数個出た確率 \end{align} ]]
と推定することができます。これは何量子ビットであっても同じで、パウリ$Z$が存在する箇所の量子ビットを測定して$1$が出た個数の遇奇の確率の差から期待値が推定できます。
4. パラメータを更新する
古典コンピュータでベイズ最適化などを用いて$\Braket{\beta_p\gamma_p|H_P|\beta_p\gamma_p}$がより小さくなるようにパラメータ$\beta_i,\gamma_i$を更新します。
5. 1〜4を繰り返し、最適なパラメータを得る
6. 最適なパラメータにおける終状態を測定する
5で得た最適なパラメータを適用した状態$\ket{\beta_p^{*}\gamma_p^{*}}$に対して、$Z$基底で測定を行います。測定は複数回行い、最もエネルギーの小さい解を採用します。
QAOAの発展:QAOA+
QAOAのミキサーハミルトニアン$H_M$は基本のパウリ$X$以外にもいくつか候補があり、問題の性質に応じて適切なものを選択するとより効率的に解を探索する事ができます。
例えば通常のQAOAは最適化問題の制約条件を満たさない解も含めた全空間を探索しますが、QAOA+(Quantum Alternating Operator Ansatz) と呼ばれる手法は、QAOA(Quantum Approximate Optimization Algorithm)のミキサーハミルトニアン$H_M$を問題に合わせたものに変更することで 特定の制約条件を満たした解のみを探索 するように修正したものです。
特に$XY$ゲートを使用したものが有名で、これは$\ket{10}\to\ket{01}$といったように2つの量子ビットの値を入れ替えるSWAPゲートでもあります。
[[ \begin{align} \frac{X_1X_2+Y_1Y_2}{2}=SWAP \end{align} ]]
$X$ゲートの代わりにこの$XY$ゲートを用いると$\ket{10}$と$\ket{01}$が交互に入れ替わるような時間発展が起き、$\ket{00}$や$\ket{11}$は発生しません。このような状況は、複数の量子ビットの内D個のみが$1$となるように制限をもたせる等式制約$\sum_{i=1}^NZ_i=D$を実装する際に非常に便利で、初期状態で量子ビットD個だけを$\ket{1}$としておけば、量子ビット間でD個しかない$\ket{1}$の交換のみが生じ、常に$\sum_{i=1}^NZ_i=D$制約が満たされたまま探索が行われることになります。
等式制約$\sum_{i=1}^NZ_i=D$に対するミキサーハミルトニアン$H_M$は以下のように、$Z_i-Z_{i+1}$間のSWAP演算子を足し合わせたものになります。
[[ \begin{align} H_M = \sum_{i=1}^N\frac{X_iX_{i+1}+Y_iY_{i+1}}{2}+\frac{X_NX_1+Y_NY_1}{2} \end{align} ]]
このようにミキサーハミルトニアンを柔軟に設定できる点がQAに比べてQAOAの強みとなっています。
具体例:ポートフォリオ最適化
解説
QAOAによる組合せ最適化の具体例として、ここでは ポートフォリオ最適化 について解説します.
ここで扱うポートフォリオ最適化問題とは、N通りの株式銘柄のうち、銘柄$i$を買うのか($z_i=1$)買わないのか($z_i=0$)、その選択をリスクとリターンのバランスを考慮して最適化することを目的としています。ここではMarkowitzモデルと呼ばれる以下のコスト関数を最小化することとして問題を定式化します:
[[ \begin{align} U=\lambda\sum_{i=1}^N\sigma_{ij}z_iz_j-(1-\lambda)\sum_{i=1}^N\mu_iz_i \end{align} ]]
右辺第1項は投資リスクを表す項、第2項は投資リターンにマイナスをかけた項で、各パラメータや変数の意味は以下の通りです。
- $z_i$ : 資産$i$の保有状態(保有:1、未保有:0)
- $\lambda$:リスクとリターンのバランスを調整するパラメータ(0から1の範囲)
- $\sigma_{ij}$:資産$i,j$のリターンの共分散
- $\mu_i$:資産$i$の期待リターン
リターン項ではその銘柄を保持した際の期待リターンをそのまま足し合わせており、リスク項では共分散から株価が連動する銘柄を同時保有するのはリスクと見なされペナルティがかかるようになっています。
また、銘柄の合計保有数は以下の制約を満たす必要があります:
[[ \begin{align} \sum_{i=1}^Nz_i = D \end{align} ]]
ここで、$D$は所望の合計保有サイズです。
これをソフト制約として表すにはコスト関数に以下のようなペナルティ項を足します。
[[ \begin{align} P= A\left(\sum_{i=1}^Nz_i-D\right)^2 \end{align} ]]
また、前述のQAOA+からXYミキサーハミルトニアンを用いてこの制約をハード制約として表現することもできます。
まず初期状態として合計保有サイズが$D$となり、かつXYミキサーハミルトニアンの基底状態となるような状態を作成します。例えば$D=3$では以下のように1がD個、0がN-D個となるすべての状態を同じ重みで重ね合わせた状態が初期状態として使用できます。
[[ \begin{align} \ket{\psi_0} = \frac{1}{\sqrt{_NC_D}}(\ket{00111}+\ket{01011}+\ket{01101}+...+\ket{11100}) \end{align} ]]
この状態はXY、すなわちSWAP演算子を作用させたとき、内部で状態の入れ替わりが起き、全体として変化しないため基底状態であり、かつ常に$\sum_{i=1}^Nz_i = 3$を満たす基底のみで構成されており制約を満たしています。
従ってミキサーハミルトニアンとして$z_i-z_{i+1}$間のスワップ演算子(終端の$z_N-z_1$間も)を用意することで、状態$\ket{1}$の位置が移動するだけで総数変わらずは常に保有銘柄数$D$が保たれた空間に限定された探索が行われることになります。
Qiskitによるシミュレーション
ここではQiskitを用いてQAOAとQAOA+によるポートフォリオ最適化を実際に実装してシミュレーションを行います。
まずは以下の必要なライブラリをインストールしてください。
pip install qiskit==1.2.4 qiskit-algorithms==0.3.1 qiskit-optimization==0.6.1
必要なライブラリをインポートします。
#必要なライブラリのインポート
import numpy as np
import itertools
from qiskit import QuantumCircuit
from qiskit.primitives import Sampler
from qiskit.quantum_info import SparsePauliOp
from qiskit_algorithms import QAOA
from qiskit_algorithms.optimizers import COBYLA
from qiskit_optimization import QuadraticProgram
from qiskit_optimization.algorithms import MinimumEigenOptimizer
問題設定である各種パラメータ$\mu_i,\sigma_{ij},\lambda,D$を定義します。
# 資産の期待リターン
mu = np.array([0.24, 0.20, 0.15, 0.10, 0.18])
# 資産の共分散行列
sigma = np.array([
[0.1, 0.02, 0.04, 0.01, 0.03],
[0.02, 0.08, 0.02, 0.01, 0.02],
[0.04, 0.02, 0.09, 0.03, 0.04],
[0.01, 0.01, 0.03, 0.07, 0.02],
[0.03, 0.02, 0.04, 0.02, 0.08]
])
# リスクとリターンのバランスを調整するパラメータ(0から1の範囲)
l = 0.5
# 資産数
num_assets = len(mu)
# 予算制約(選択する資産の数)
D = 3
次に量子ビットと問題ハミルトニアン、制約を定義します。
# QuadraticProgramを使ってポートフォリオ選択問題を定式化
qp = QuadraticProgram()
#量子ビットの定義
for i in range(num_assets):
qp.binary_var(name=f'z{i}')
# 問題ハミルトニアンH_pの設定
qubo_matrix = l*sigma - (1-l) * np.diag(mu)
quadratic = {}
for i in range(num_assets):
for j in range(num_assets):
quadratic[(f"z{i}",f"z{j}")] = qubo_matrix[i][j]
qp.minimize(quadratic=quadratic)
# 制約の設定:投資銘柄の合計数がDに等しくなる制約
qp.linear_constraint(linear=[1] * num_assets, sense='==', rhs=D, name='investment_constraint')
計算の初期状態として$\ket{+}^{\otimes N}$を作成します。$\ket{0}$にHゲートを作用させて作成します。
# 初期状態の設定:|0>にHゲートを作用させた|+>状態
initial_state = QuantumCircuit(num_assets)
for i in range(num_assets):
initial_state.h(i)
最後にQAOAの実行を行います。ここでのハイパーパラメータチューニングにはCOBYLA法を用いています。
# Samplerの設定
sampler = Sampler()
# QAOAの設定
p = 1 # レイヤーの深さ
cobyla = COBYLA() # ハイパーパラメータのチューニングoptimizer
cobyla.set_options(maxiter=250)
qaoa = QAOA(sampler = sampler, optimizer=cobyla, reps=p, initial_state=initial_state)
# 固有値最小化を行う
optimizer = MinimumEigenOptimizer(qaoa)
# 問題を解く
result = optimizer.solve(qp)
計算結果は例えば以下のような関数でまとめて表示することができます。
from qiskit.result import QuasiDistribution
def print_result(result,qp):
# 最適化で得られた選択結果と対応する値を取得
selection = result.x # 最適化で選ばれた選択肢。
value = result.fval # 選択に対応する最適化値。
print("Optimal: selection {}, value {:.4f}".format(selection, value))
# 最適化結果の固有状態を取得
eigenstate = result.min_eigen_solver_result.eigenstate # 固有状態に関する情報
# 固有状態の確率分布を計算
probabilities = (
# QuasiDistribution であれば、binary_probabilities メソッドを使用して確率分布を取得
eigenstate.binary_probabilities()
if isinstance(eigenstate, QuasiDistribution)
# それ以外の場合は、固有状態を辞書形式で取得して確率を計算
else {k: np.abs(v) ** 2 for k, v in eigenstate.to_dict().items()}
)
print("\n----------------- Full result ---------------------")
print("selection\tvalue\t\tprobability")
print("---------------------------------------------------")
# 確率分布を降順にソート
probabilities = sorted(probabilities.items(), key=lambda x: x[1], reverse=True)
# 各選択肢とその値、確率を表示
for k, v in probabilities:
x = np.array([int(i) for i in list(reversed(k))])
value = qp.objective.evaluate(x)
print("%10s\t%.4f\t\t%.4f" % (x, value, v))
離散分割数$p$を1とした場合、実行結果は以下のようになりました。”selection”は$Z_1\sim Z_N$の値の配列、”value”はその配列における$H_P$の値、“probability”はその配列を得る確率で、以下では確率が高い順に出力されています。
制約を満たすような$D=3$の解が高い確率で出力されている一方、$D\neq3$の解も出力されています。また最適解である$\ket{11001}$が1番高い確率で出力されているわけではありません。
Optimal: selection [1. 1. 0. 0. 1.], value -0.1100
----------------- Full result ---------------------
selection value probability
---------------------------------------------------
[0 0 1 1 1] -0.0050 0.0823
[1 0 1 1 0] -0.0350 0.0719
[1 0 1 0 1] -0.0400 0.0719
[0 1 1 1 0] -0.0450 0.0694
[0 1 1 0 1] -0.0600 0.0650
[0 1 0 1 1] -0.0750 0.0617
[1 1 1 0 0] -0.0800 0.0611
[1 0 0 1 1] -0.0750 0.0596
[1 1 0 0 1] -0.1100 0.0544
[1 1 0 1 0] -0.1050 0.0541
[1 0 1 1 1] 0.0050 0.0409
[0 1 1 1 1] -0.0150 0.0342
[1 1 1 0 1] -0.0400 0.0330
[1 1 1 1 0] -0.0450 0.0283
[0 0 1 1 0] -0.0150 0.0228
[0 1 0 1 0] -0.0650 0.0216
[1 1 0 1 1] -0.0850 0.0216
[0 0 0 1 1] -0.0450 0.0204
[1 0 0 1 0] -0.0750 0.0176
[0 0 1 0 1] -0.0400 0.0169
...
[0 0 1 0 0] -0.0300 0.0014
[0 0 0 0 1] -0.0500 0.0013
[0 1 0 0 0] -0.0600 0.0009
[0 0 0 1 0] -0.0150 0.0004
次に離散分割数$p$を$3$とした場合、実行結果は以下のようになりました。制約を満たすような解がより高い確率で出力されるようになり、また最適解である$\ket{11001}$が1番高い確率で出力されるようになりました。
Optimal: selection [1. 1. 0. 0. 1.], value -0.1100
----------------- Full result ---------------------
selection value probability
---------------------------------------------------
[1 1 0 0 1] -0.1100 0.1129
[1 1 0 1 0] -0.1050 0.1075
[1 1 1 0 0] -0.0800 0.1021
[1 0 0 1 1] -0.0750 0.0990
[0 1 0 1 1] -0.0750 0.0978
[0 1 1 0 1] -0.0600 0.0956
[1 0 1 0 1] -0.0400 0.0918
[0 1 1 1 0] -0.0450 0.0882
[1 0 1 1 0] -0.0350 0.0870
[0 0 1 1 1] -0.0050 0.0788
[1 1 1 1 1] 0.0150 0.0070
[1 1 0 1 1] -0.0850 0.0039
[1 1 1 0 1] -0.0400 0.0037
[0 0 1 1 0] -0.0150 0.0035
[0 0 1 0 1] -0.0400 0.0025
[1 1 1 1 0] -0.0450 0.0024
[0 0 0 1 1] -0.0450 0.0022
[0 1 1 0 0] -0.0700 0.0016
[1 0 1 1 1] 0.0050 0.0015
[0 1 1 1 1] -0.0150 0.0014
...
[0 1 0 0 1] -0.0900 0.0007
[0 0 0 0 1] -0.0500 0.0004
[1 0 0 0 0] -0.0700 0.0003
[0 0 0 0 0] 0.0000 0.0002
次にSWAPゲートを利用してハード制約を実装したQAOA+を実装してみます。
QAOAのときとは異なり制約は実装せず、代わりにミキサーハミルトニアンとして$Z_i-Z_{i+1}$間のSWAP演算子、すなわち$\frac{XX+YY}{2}$を用意します。
# QuadraticProgramを使ってポートフォリオ選択問題を定式化
qp = QuadraticProgram()
#量子ビットの定義
for i in range(num_assets):
qp.binary_var(name=f'z{i}')
# 問題ハミルトニアンH_pの設定
qubo_matrix = l*sigma - (1-l) * np.diag(mu)
quadratic = {}
for i in range(num_assets):
for j in range(num_assets):
quadratic[(f"z{i}",f"z{j}")] = qubo_matrix[i][j]
qp.minimize(quadratic=quadratic)
#ミキサーハミルトニアンの設定
mixer = SparsePauliOp(["XXIII", "YYIII", "IXXII", "IYYII", "IIXXI", "IIYYI", "IIIXX", "IIIYY", "XIIIX", "YIIIY"], [1/2, 1/2, 1/2, 1/2, 1/2, 1/2,1/2, 1/2, 1/2, 1/2])
次に初期状態として$\ket{1}$が$D$個、$\ket{0}$が$N-D$個の全状態の重ね合わせを用意します。
#初期状態の設定
# itertools.permutationsを使い、1がD個,0がN-D個のすべての組み合わせを取得
target_states = list(set("".join(seq) for seq in itertools.permutations("1"*D+"0"*(num_assets-D))))
# 各状態の振幅を計算(均等な重ね合わせなので√(1/数)で割る)
amplitude = 1 / np.sqrt(len(target_states))
# 2^num_assets次元の状態ベクトルを用意し、対象の状態にのみ振幅を割り当てる
np_initial_state = np.zeros(2**num_assets, dtype=complex)
for state in target_states:
index = int(state, 2) # 状態を整数(インデックス)に変換
np_initial_state[index] = amplitude # 対象の状態に振幅を設定
# 回路の作成と初期化
initial_state = QuantumCircuit(num_assets)
initial_state.initialize(np_initial_state)
QAOAモジュールに作成したmixerを渡して計算を実行します。mixerの指定がない場合はデフォルトでパウリXがミキサーハミルトニアンとなります。
# Samplerの設定
sampler = Sampler()
# QAOAの設定
p = 3 # レイヤーの深さ
cobyla = COBYLA()
cobyla.set_options(maxiter=250)
qaoa = QAOA(sampler = sampler, optimizer=cobyla, reps=p,initial_state=initial_state,mixer=mixer)
# 最適化アルゴリズムとしてQAOAを使用
optimizer = MinimumEigenOptimizer(qaoa)
# 問題を解く
result = optimizer.solve(qp)
離散分割数$p$を$3$とした場合、実行結果は以下のようになりました。制約を満たすような解のみが出力される様になっており、ミキサーハミルトニアンがハード制約として機能している事がわかります。
Optimal: selection [1. 1. 0. 0. 1.], value -0.1100
----------------- Full result ---------------------
selection value probability
---------------------------------------------------
[1 1 0 0 1] -0.1100 0.3638
[1 0 1 0 1] -0.0400 0.1743
[0 1 1 0 1] -0.0600 0.1382
[1 1 1 0 0] -0.0800 0.0931
[1 1 0 1 0] -0.1050 0.0924
[0 1 1 1 0] -0.0450 0.0548
[1 0 0 1 1] -0.0750 0.0452
[1 0 1 1 0] -0.0350 0.0200
[0 1 0 1 1] -0.0750 0.0116
[0 0 1 1 1] -0.0050 0.0066
終わりに
本記事ではQAOAの基本から実応用までを解説してきました。QAOAは量子アニーリングから着想を得た、ゲート式量子コンピュータ上で実行する、最適化問題を解くためのアルゴリズムで、現行のノイズがあってかつ規模の小さいデバイスでも実行可能となっています。従ってQAOAは量子コンピューティングが実世界の課題を解決するための一歩となる可能性を秘めています。
http://www.msi.co.jp NTTデータ数理システムができること
- ゲート型量子コンピュータの基礎
- 量子アルゴリズム ~アダマールテスト~
- 量子アルゴリズム ~量子フーリエ変換~
- 量子アルゴリズム ~量子位相推定~
- 量子アルゴリズム ~Shorのアルゴリズム~
- 量子計算による最適化アルゴリズム~QAOA~










