ゲート型量子コンピュータの基礎

この記事では ゲート型 、所謂 量子回路モデル型 の量子コンピュータについて、その基礎と代表的なアルゴリズムについて解説します。

量子コンピュータでは素因数分解やデータ探索、連立一次方程式の解を求める問題など、科学技術計算を通して実社会にも影響する重要な問題を、従来のコンピュータよりも遥かに高速に解くことができます。

量子コンピュータとは何か

1900年代初頭、観測技術の発展によりそれまで物理学を支配していたニュートン力学やマクスウェル電磁気学などの所謂「 古典論 」ではうまく説明できない事象が次々と発見され始めました。それは私たちの世界を形づくる原子や分子といったミクロの世界の出来事で、これら小さな粒子はマクロな世界を生きる私たちの直感に反するような不思議な性質を持っています。そうした小さな粒子である「 量子 」の不思議な性質を説明するために考えられたのが「 量子論 」です。量子論は古典論が説明が困難であった物理現象を見事に説明し、自然界が量子によって成り立っていることを示しました。

私たちは現在、様々な物理現象を計算機を用いてシミュレートし、予報や実験の代用として広く活用していますが、量子の世界をシミュレートしようとするとある問題が生じます。量子には複数の状態を同時に取りうる「 重ね合わせ 」という性質があるため、1つの量子の状態を記述するためは多くのリソースが必要となります。しかし、私たちが従来使用している所謂「 古典コンピュータ 」では、０と１どちらかの状態しか保持できない「 古典ビット 」が用いられているため、重ね合わせを有する量子の世界を記述するのに非効率となります。従って多数の量子が存在する問題を古典コンピュータで解こうとすると、時間・空間的に必要なリソースが指数的に増大してしまい、現実的に解くことができないのです。

そこでその解決策として、量子をリソースとして利用することで計算する「 量子コンピュータ 」が考案されました。自然界が量子論で動いているのであればそれを効率的にシミュレートするためのコンピュータも量子論の原理で設計されているべきということです。量子コンピュータでは情報は０ と１両方の状態を 同時に とることができる「 量子ビット 」で表現されます。量子コンピュータ上で実行される計算を「 量子計算 」といい、量子ビットを用いて多数状態を同時に扱い、その結果をうまく処理することで、量子系のシミュレーションだけでなく 素因数分解 などのいくつかの社会的に有用な問題を、 古典コンピュータと比べて非常に高速 に解くことができます。

今回は ゲート型 、所謂 量子回路モデル型 の量子計算についての基礎を解説します。量子計算を実行するにはゲート型以外にも量子チューリングマシン、測定型量子計算、トポロジカル量子計算、断熱量子計算などがあり、これらは互いに多項式時間のオーバーヘッドのみでシミュレート可能なため計算能力は等価とされています。

※多項式時間：問題の大きさを示す因子$N$の多項式で表される計算時間。多項式時間で処理可能な場合、現実的な計算時間で計算可能とみなされる。

ゲート型量子コンピュータの基礎

ここではゲート型量子コンピュータの以下の基本要素について、古典コンピュータと比較しながら解説します。

• 量子ビット
• 測定
• 量子ゲート

量子ビット

古典ビットは1ビットあたり０と１の2通りの状態を表すことができます。さらに$n$ビットあれば$2^n$通りの状態を表すことができます。しかし当然、1度に表せる状態はその中の1つだけという制限があります。

一方、量子ビットでは1ビットで０と１の両方の状態を同時に保持することができます。1量子ビットの状態は複素数 $\alpha, \beta$ を用いて次のように表現できます。

[[ \begin{align*} 1{\bf 量子ビット状態\;:\;} \ket{\psi_1} &= \alpha \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \beta \begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ &= \alpha \ket{0} + \beta \ket{1} \;\;\;\; (\alpha, \beta \in \mathbb{C}) \end{align*} ]]

1量子ビットの状態は2次元のベクトルとして表され、その正規直交基底として $\begin{pmatrix} 1 \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ 1 \end{pmatrix}$ がそれぞれ古典ビットの０と１に対応しています。また、ベクトルによる表現の代わりに $\ket{0},\ket{1}$ といった ブラケット記号 を用いて表現されることが多いです。複素係数 $\alpha, \beta$ は 0 と 1 の重なりの程度を表しています。

複数量子ビット状態は1量子ビット状態のテンソル積で表現され、2量子ビットの場合は $\ket{0}\otimes\ket{0}$ や省略記として $\ket{0}\ket{0}$ や $\ket{00}$ のように表記します。

[[ \begin{align*} 2{\bf 量子ビット状態\;:\;}\ket{\psi_2} &=\alpha\begin{pmatrix}1\\0\\0\\0\end{pmatrix}+\beta\begin{pmatrix}0\\1\\0\\0\end{pmatrix}+\gamma\begin{pmatrix}0\\0\\1\\0\end{pmatrix}+\delta\begin{pmatrix}0\\0\\0\\1\end{pmatrix} \\ &=\alpha\ket{00}+\beta\ket{01}+\gamma\ket{10}+\delta\ket{11}\;\;\;\;(\alpha,\beta,\gamma,\delta\in\mathbb{C}) \end{align*} ]]

従って、2量子ビットであれば $\ket{00}, \ket{01}, \ket{10}, \ket{11}$ の4通り、$n$量子ビットあれば$2^n$通りの状態の重ね合わせが表現できます。

測定

古典ビットは状態が０であれば、私たちが何か手を加えたりしない限り、いつ見ても状態が０のままで突然１に入れ替わったりしません。

しかし量子ビットでは観測者である私たちがそれを観測する、「 測定 」という操作を行うまでは状態が０か１のどちらかに定まっていません。全く同じ操作を行ったとしても、時として０や１が確率的に表れるわけです。1量子ビット状態において測定を行った際に０１が現れる確率は下図のようになります。

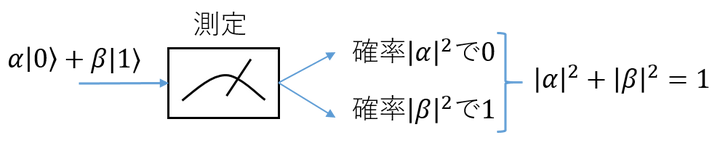
当然０になる確率と１になる確率は合計して1になる必要があるため、複素係数 $\alpha, \beta$ には $|\alpha|^2+|\beta|^2=1$ という制約があります。これは状態をベクトル表示した際の $\begin{pmatrix}\alpha \\ \beta\end{pmatrix}$ の長さが1であることと等価です。

さらに測定という操作を行うと元の状態は壊れてしまい、測定に対応した状態に変化します。例えば測定の結果０が得られた場合、状態は $\ket{0}$ となり、以降は何度測定しても０しか得られなくなります。

量子ゲート

古典コンピュータでは各古典ビットに対する AND, OR, NOT などのゲート(素子)を組み合わせてあらゆる計算を表現しています。

量子コンピュータにおける計算も、細かく分割していくと「 量子ゲート 」と呼ばれる、量子ビットの状態を別の状態に移すような操作の組み合わせで成り立っています。量子ビットの状態がベクトルで表されるため、量子ゲートの操作はベクトルに作用する 行列形式 で表現されます。

例えば $\ket{0}$ と $\ket{1}$ を入れ替える「Xゲート」は次のように表されます。 [[ X=\begin{pmatrix}0&1\\1&0\end{pmatrix} ]] 量子ゲートでは量子ビットで表現された重ね合わせ状態を同時に操作することができます。 [[ X(\alpha\ket{0}+\beta\ket{1})=\alpha\ket{1}+\beta\ket{0} ]] 次に量子ビットが複数ある場合を考えます。下図では2量子ビット状態の「1つ目の量子ビット」に、Ｘゲートを作用させています。

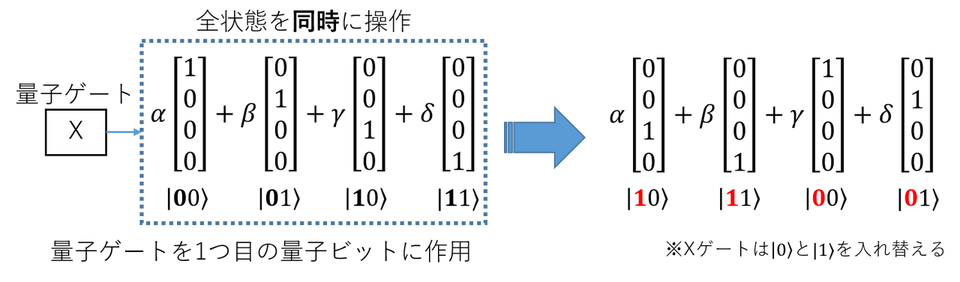
1つの量子ビットに作用する量子ゲートは前述の通り $2\times2$ の行列で表されます。しかし、上図のように2量子ビット状態に作用する量子ゲート行列のサイズはベクトルの長さに合わせて $4\times4$ でないといけません。このような場合は、2つ目の量子ビットに対して何も変化を起こさないように $2\times 2$ の恒等行列 $I$ を持ってきて $X$ とテンソル積を取ります。 [[ \begin{align*} XI &= X \otimes I = \begin{pmatrix}0&1\\1&0\end{pmatrix}\otimes\begin{pmatrix}1&0\\0&1\end{pmatrix} \\ &=\begin{pmatrix}0*I&1*I\\1*I&0*I\end{pmatrix} = \begin{pmatrix}0&0&1&0\\0&0&0&1\\1&0&0&0\\0&1&0&0\end{pmatrix} \end{align*} ]] このように複数量子ビット状態内の特定の量子ビットに個別に作用する量子ゲートはテンソル積で表現できます。例えば、 $XXX$ と書いた場合は3つの量子ビットにそれぞれ個別にXゲートが作用する $8\times8$行列となっています。また、後述する「CNOTゲート」のように元々2量子ビットに作用する$4\times 4$行列の量子ゲートや、それ以上のサイズの量子ゲートも存在します。

量子ゲートには、作用させる前後で全状態の確率の和が保存されていなくてはならない、という制約があります。つまり、ある量子ビットに対して量子ゲートを作用させた際、0と１の出る確率の配分(複素係数)は変わっても良いですが、確率の和を取ったらやはり1になっていないと整合性がとれない、ということです。

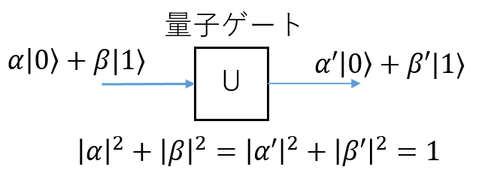
これは作用させたベクトルの長さを変えないことと同値であり、このような性質を満たす行列を「ユニタリ(unitary)行列」と言います。量子ゲートは全てこのユニタリ行列で構成されている必要があります。これは複数量子ビットに渡る量子ゲートにおいても同様で、作用させた量子ビット全体で確率が保存されている必要があります。

さらに古典コンピュータとの違いとして、例えば古典のANDゲートでは2つの入力に対して出力は1つのみとなりますが、量子ゲートではそうした入出力の数が異なるものは構成できません。古典のANDゲートでは出力から入力を復元することができないため、ゲート操作により 情報が損失 してしまっています。量子ゲートはそういった情報の損失が生じるような操作を許さず、常に 可逆的 (逆行列に対応する操作で元に戻せる)となっています。ユニタリ行列は逆行列を必ず持ちます。

量子回路図

量子計算は量子ビットに対して量子ゲートと測定という操作を組み合わせて順次行っていくことで実行されます。そうした操作の流れを記述したものを 量子回路図 といい、以下のように描かれます。

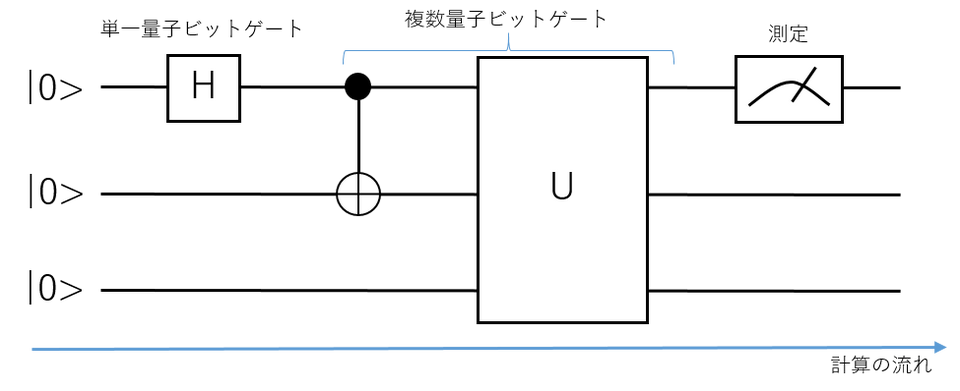
横に伸びる各ワイヤーが1つ1つの量子ビットを表しており、左端にはそれぞれの初期状態が記載されています。量子ゲートや測定といったパーツはボックスや、縦に繋がるワイヤーで表現されます。量子回路では時間は左から右に流れるため、 量子ゲートは左から作用させる時系列順に並べられ、作用された量子状態が左から右に移動し、各ゲートを通過していきます。

ユニバーサルゲートセット

古典コンピュータではNANDゲートを組み合わせることであらゆる計算が表現できることが知られています。

量子コンピュータでも同様に、以下に紹介する {H, T, CNOT} の3種類の量子ゲートがあれば任意の量子ゲートを任意の精度で近似して実行できることが知られています。これを「 ユニバーサルゲートセット 」といい、ユニバーサルゲートセットを揃えた量子コンピュータを「 万能量子コンピュータ 」と言います。

※ユニバーサルセットは一意ではありません。ここで紹介するのは代表的なユニバーサルゲートセットです。

Hゲート

アダマール (Hadamard)ゲートは1量子ビットに作用し、主に $\ket{0}$ や $\ket{1}$ を等確率の重ね合わせ状態に変換する操作を行います。 [[ H\ket{0}=\frac{\ket{0}+\ket{1}}{\sqrt{2}}=\ket{+} \\ H\ket{1}=\frac{\ket{0}-\ket{1}}{\sqrt{2}}=\ket{-} ]] 上式のように重ね合わせ状態 $\frac{\ket{0}+\ket{1}}{\sqrt{2}}$ は $\ket{+}$, $\frac{\ket{0}-\ket{1}}{\sqrt{2}}$ は $\ket{-}$ と表記されます。

Tゲート

Tゲートは$\pi/4$位相ゲートとも言い、1量子ビットに作用し、 $\ket{0}$ と $\ket{1}$ の複素係数の 位相差 に $\pi/4$ を追加する操作を行います。位相差は相対的なものなので、基本的には $\ket{1}$ 側に押し付けてしまいます。 [[ {T}(|\alpha|e^{i\theta}\ket{0}+|\beta|e^{i\phi}\ket{1}) =|\alpha|e^{i\theta}\ket{0}+|\beta|e^{i(\phi+\pi/4)}\ket{1} ]] HゲートとTゲートがあれば任意の単一量子ビットゲートが表現できます。

CNOTゲート

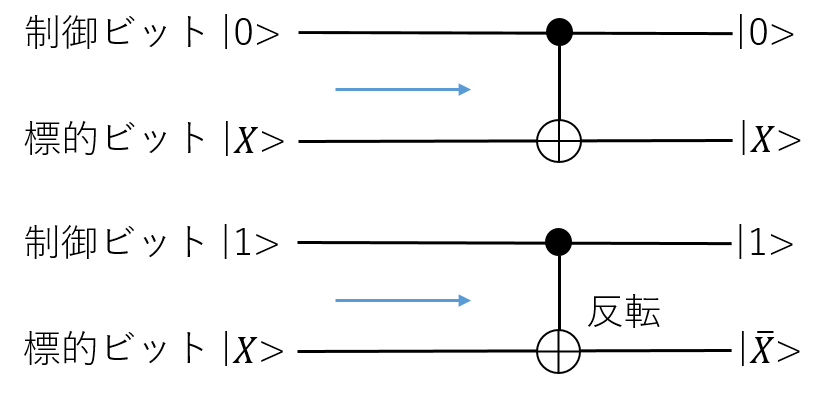
CNOTゲートは 制御 と 標的 と呼ばれる2量子ビットに作用し、制御に対応する量子ビットが０の時は何もせず、１の時は標的に対応する量子ビットの値を反転する操作を行います。 [[ \text{CNOT}\ket{0}\ket{x}=\ket{0}\ket{x} \\ \text{CNOT}\ket{1}\ket{x}=\ket{1}\ket{\bar{x}} ]] ここで $\bar{x}$ は $x$ を反転した状態を表します。CNOTと任意の単一量子ビットゲートがあれば任意のn量子ビットゲートが表現できます。

量子アルゴリズム

量子ビットは重ね合わせによって多数の状態を同時に表現できると紹介しました。例えば$n$個の量子ビットがあれば$2^n$個の状態を表現でき、量子ゲートによってそれらの状態を同時に操作することが可能です。これはあたかも古典コンピュータと比べて並列な分$2^n$倍高速に計算ができているかのように思えます。しかし、実はそれは大きな誤りです。

測定の節でも説明したように、計算の結果は観測によってどれか1つしか得られません。欲しい状態(答え)が1つの場合、特に 工夫もなく 計算を行うと確率$1/2^n$程度でしかその状態は得られません。従って、欲しい状態を確実に得るためには結局同じ計算を$2^n$回程度繰り返す必要があり本末転倒となってしまうわけです。

従って、 欲しい状態が高確率で得られる ように問題の構造などを利用してうまく設計されたアルゴリズムでなければ量子計算によって高速化はなされません。そうしたアルゴリズムを「 量子アルゴリズム 」と呼びます。

以下に代表的な量子アルゴリズムをいくつか紹介します。

アダマールテスト

概要：ユニタリ行列を入力の量子状態(ベクトル)に作用させた際の 期待値を推定する 。

古典コンピュータで行おうとすると行列サイズが量子ビット数に対して指数的に大きくなるため現実的に解くのが難しいですが、量子コンピュータでは量子ビット数に対して高々多項式回のサンプリングで近似することができます。

アダマールテストを行うとユニタリ行列を作用させる入力の量子状態は変化します。しかし、変化した状態をさらに入力として何度もアダマールテストを繰り返していくと、入出力が同じ状態へと収束し、その状態はユニタリ行列の固有状態となります。従って、繰り返し実行することで結果的に固有値も推定することができます。また、固有状態を入力として用いた場合はその状態を壊すことなく固有値を測定する、「 間接測定 」として利用することができます。

量子フーリエ変換

概要： 離散フーリエ変換 を行う。

量子位相推定など様々な量子アルゴリズムのサブルーチンとして用いられることが多いです。

古典コンピュータ(高速フーリエ変換)では標本数$N$に対してに$\mathcal{O}(N\log N)$かかるところ、$\mathcal{O}((\log N)^2)$に減らすことができます。

量子位相推定

概要：ユニタリ行列の 固有値を推定する 。

ユニタリ行列の固有値は大きさ１の複素数なため、$e^{i\theta}$と書けば位相$\theta$を求めることは固有値を求めるのと同値なため「 位相推定 」と呼ばれます。

アダマールテストによる固有値推定では入力状態が固有状態に収束するまでに多くの繰り返しが必要となります。アダマールテストでは入力状態を表現する量子ビットの他に、計算のため補助量子ビットを1つ使用しているのですが、量子位相推定ではこの補助量子ビットを複数に拡張することで必要な繰り返し回数を大幅に下げることができます。

Shorのアルゴリズム

概要：素因数分解を行う。

ある整数Nを素因数分解したいとすると、まずNと互いに素な整数$x$を(ユークリッドの互除法などで)選んできます。次に $x^r=1(mod\;N)$ となるような最小の整数 $r$ 、すなわち 位数 を見つけます。この「 位数発見問題 」を量子計算にて行います。詳細は省きますが、この位数発見問題は特殊なユニタリ行列の固有値を求める問題に帰着させることができ、量子位相推定にて固有値を求めます。因数 $r$ が偶数の場合(奇数の場合は $x$ を選びなおし)は高い確率で $x^{r/2}\pm1$ のどちらかが N と非自明な公約数( N の因数)を持つことになります。 N を得られた因数で割って分割し、因数、割られた数それぞれにアルゴリズムを再帰的に適用することで素因数分解が完了します。

素因数分解を $N$ の桁長 $n$ に対して多項式時間で解く古典アルゴリズムは未だに見つかっていませんが、Shor のアルゴリズムでは $\mathcal{O}(n^3\log n)$ で計算することができます。

Grover探索

概要：整列化されていないデータベースから特定のデータを 探索 する。

$N$個の要素から例えば $f(x)=1, x\in \mathbb{N}$となる要素を探索する問題です。指数加速ではありませんが、古典コンピュータによる線形探索では $\mathcal{O}(N)$ かかるところ、 $\mathcal{O}(N^{1/2})$ の加速となります。

Harrow-Hassidim-Lloyd (HHL) アルゴリズム

概要：連立1次方程式を解く(逆行列の計算)。

HHLアルゴリズムは、連立方程式 $A\vec{x}=\vec{y}$ の解である $\vec{x}=A^{-1}\vec{y}$ 、を高速に探索する量子アルゴリズムです。

古典コンピュータによる現在の最良のアルゴリズムでは行列Aのサイズ $N\times N$ に対して $\mathcal{O}(N)$ かかるところ、 $\mathcal{O}(\text{poly}(\log N))$ の指数加速となります。ただし、条件として行列$A$がスパース(非零成分が少ない)である必要があります。また、初期状態として $\vec{y}$ に対応するような量子状態を用意できた前提でのアルゴリズムなため、この状態を用意するために $\mathcal{O}(N)$ の時間がかかると意味がありません。従って、何らかの量子計算によって得られた量子状態をそのまま $\vec{y}$ として使用するような状況が想定されます。

おわりに

この記事ではゲート型量子コンピュータの基礎について解説しました。今回紹介したような量子アルゴリズムを実行できるような、理想的な量子コンピュータの実現にはまだまだ課題があり、技術的なブレイクスルーが待たれます。しかし着実に古典コンピュータを超えるような結果が得られる段階まで来ており[1]、今後の発展が注目されています。

今後の記事では量子コンピュータの実現に不可欠な「誤り訂正符号」や、ノイズのある量子コンピュータでも実行可能な「NISQ」アルゴリズムについて紹介していく予定です。

参考文献

• Kim, Youngseok, et al. "Evidence for the utility of quantum computing before fault tolerance." Nature 618.7965 (2023): 500-505.