- HOME
- 統計解析とは？統計解析と機械学習の違い、統計解析の使いどころ
2020年6月 3日 19:07
統計解析の特徴
統計解析とは統計学的理論に基づいて蓄積されたデータに対する分析を行うことです。 蓄積されたデータを使用して予測や分析を行うという意味で機械学習とよく似ています。 機械学習全盛の昨今では、単に統計解析のできることを考えても「それって機械学習でやることでは？」という話になってしまいますので、本記事では機械学習との比較ということを強く意識して考えてみます。
機械学習と比較して統計解析の強み・特徴は次のような点だと思います。
少量のデータでも分析しやすい
有限の観測データ（標本、サンプル）からその集団全体（母集団）が持っている傾向、バラつきなどを明らかにすることが統計解析の伝統的なタスクです（例：選挙の出口調査、新聞社の世論調査）。統計解析では、有限のデータから得られる情報やデータの集め方について数学モデルに基いた判断が可能になります。
統計解析においても機械学習においても「データは多ければ多いほど良い」というのは事実ではありますが、統計解析的アプローチを活用して「今使えるボリュームのデータで分かること」も理解しておくと実践的な打ち手を増やすことができます。
モデルの解釈がしやすい
統計解析モデルは統計的に意味のある比較的シンプルな式で記述されることが多いため、モデルの意味やパラメータの意味を人間が後から解釈しやすい場合が多いです。線形回帰モデルの回帰係数は解釈しやすいパラメータの典型例です。
機械学習はブラックボックスで解釈しにくいという指摘を受けることが多いですが、解釈性を重視したい分析の場合には統計解析は有力な選択肢になり得ます。
予測値や推定値のバラつき（誤差）を評価しやすい
データやモデルが統計学的に扱いやすい分布に従うことを仮定して分析するため、推定されるパラメータや予測値の誤差の分布も扱いやすいものになる場合が多いです。
例えば数値予測を行う場合、下記のグラフのように予測値の他に95%信頼区間（95%の確率で予測値がこの範囲に収まる領域）を推定できます。
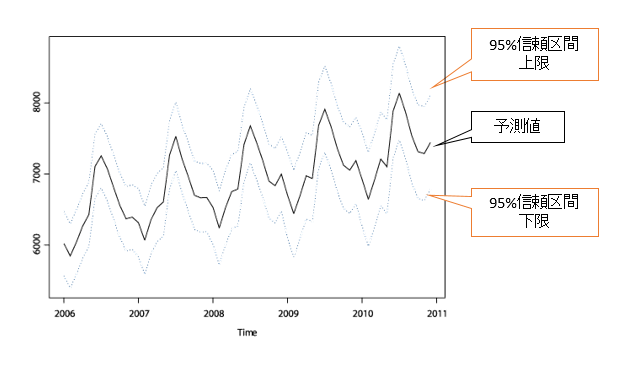
統計解析の手法
線形回帰
統計解析の手法として最も有名なのが線形回帰です。 次のビールの販売量と最高気温の関係の表から、下図の赤線のような関係を導く分析です。
| 最高気温（℃） | 販売量（ケース） |
|---|---|
| 18 | 24 |
| 20 | 27 |
| 22 | 29 |
| 25 | 30 |
| 28 | 36 |
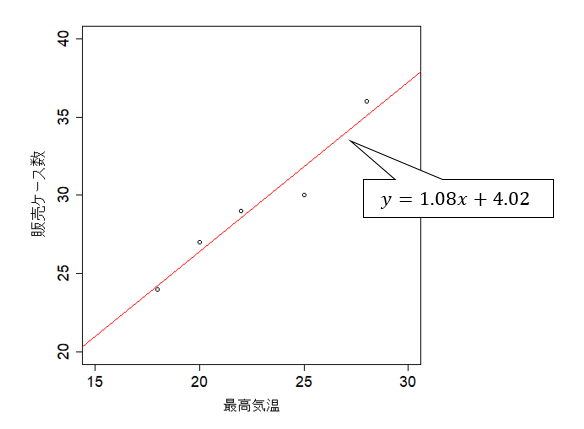
最高気温が1℃高くなるとビールの販売量が1.08ケース増えると理解することができます。 これを予測モデルと考えれば、天気予報に基づいて販売量を予測して入荷数を調整することができるようになります。
上の例は1つの変数のみで予測する単回帰モデルですが、さらに曜日、イベント、予約人数などの変数を追加した重回帰モデルにすることでもう少し複雑な状況を表現することもできます。 モデル式を少し変えることで、異常が発生するかどうかや商品を購入するかどうかなどを予測するロジスティック回帰モデルや、事故発生回数などを予測するポアソン回帰モデルへと応用することもできます。
いずれのモデルでも、○○が上がれば××が上がる（下がる）という人間にとって解釈しやすい一次方程式で表現されるため、予測だけでなく構造や要因の理解のためにも幅広く使われています。
主成分分析
主成分分析は次元縮約手法の1つです。 項目数の多い高次元のデータを理解することは難しいですが、本質的に重要な情報を抽出して次元を下げることで分析や解釈をしやすくします。
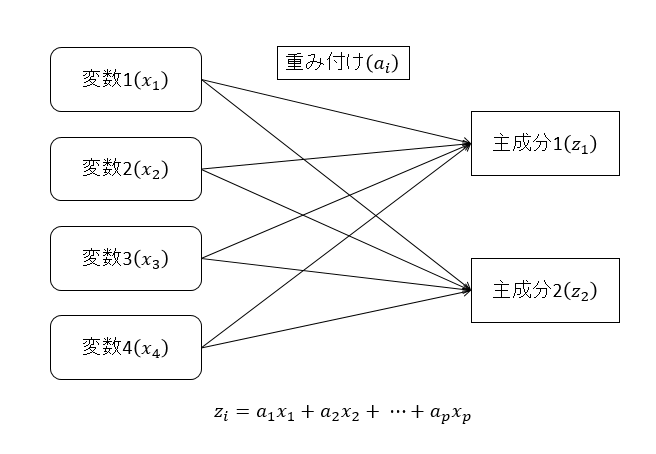
例えば設備のセンサーデータの場合、ある個所の温度を上げれば連動して周辺の別の箇所の温度や圧力が変動します。 このような場合1つの連動する系のデータは1つにまとめてしまった方が理解しやすそうです。 このように、複数の変数を1つの主成分と呼ばれる情報にまとめてしまうのが主成分分析です。 下図のように、高次元空間のうちの分散の大きい（意味のある）部分空間を抽出していると解釈することもできます。
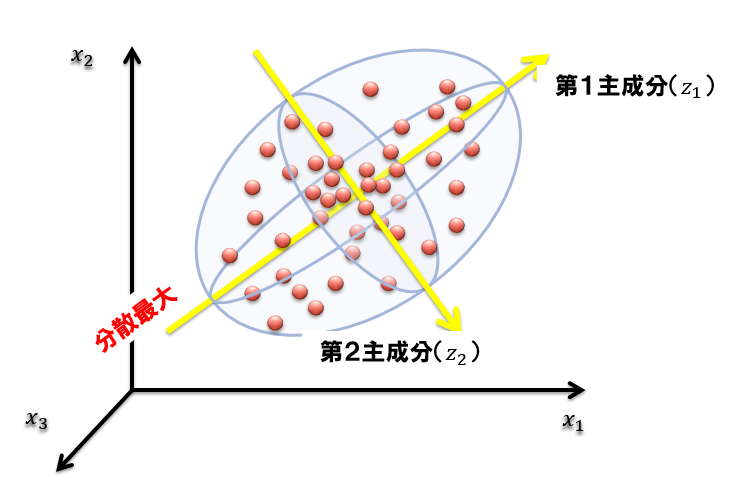
情報量の大きい主成分を使用して散布図を作成してデータの様子を可視化したり、各レコードがどのような特徴を持つものかを解釈することができるようになります。
混合ガウスモデル
混合ガウスモデルでは、データが複数の正規分布の重ね合わせで生成されていると仮定して、データに適合する正規分布の組み合わせを推定します。
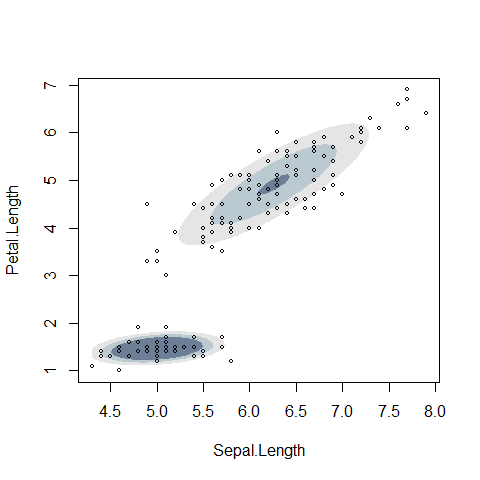
上のグラフでは、上側と左下の2つの正規分布の重ね合わせになっていると考えるとデータにうまく適合すると判断されたようです。 各データに対してそれぞれの正規分布への所属確率を出すことができるため、ソフトクラスタリングアルゴリズムとして使用することができます。 また、どの正規分布にも所属確率が高くないデータを外れ値と考えれば、外れ値検出アルゴリズムとして使うこともできます。
統計解析と機械学習の違いは何？
昨今の AI ブームの中で機械学習（特に Deep Learning）が注目を浴びていますが、実際の分析では同じような状況で統計解析的なアプローチも広く使われています。 どのように違いどのように使い分ければ良いのでしょうか。
機械学習と統計解析のそれぞれの起源を振り返ってみましょう。 統計解析はコンピューターが生まれる前の大昔の人口統計や経済統計から始まっており、入手できた有限のサンプルから実態を把握することを目指していました。 機械学習はコンピューターの発明後に人工知能（AI）の一分野として発展してきたもので、データから学習した結果に基づいて知的に動作するシステム（AI）の作成を目指していました。 現在では両者の垣根は低くなっており、同じようなアルゴリズムを使用して同じようなタスクに取り組むケースも多いですが、上記のような歴史的経緯による考え方の違いが残っていると感じます。
必要なデータ量
統計解析はコンピューター以前の手計算の時代から考えられているため構造が比較的シンプルで少量のデータでも問題なく適用できる手法が多いです。数百、数千件オーダーのデータに対しても（主にデータの分布に関する）仮定を満たせば適切に推論して結論を導くことができます。
一方で、現在よく使われる機械学習的なアルゴリズムは構造が複雑で、大量のデータを使用して学習することが期待されているものが多いです。特別な事情がなければ少なくとも数万件オーダーのデータを、可能であればもっと大量のデータを学習に使いたいというのが機械学習で使用するデータに対する感覚です。複雑な構造の内部パラメータに大量のデータの情報を反映できるため、十分なデータを使用することができれば、シンプルな構造の統計的手法よりも高精度な予測・分析ができる可能性が高いです。
モデル構造に対する解釈を考えるか
統計解析では「こういう構造であると辻褄が合うのではないか」という仮説に対してデータをあてはめるため、仮説の妥当性を検証するためにもモデルの内部構造そのものに関心があり、何らかの解釈を与えようとする場合が多いです。上で挙げた手法でも、何か解釈可能なモデルが出来上がって、それを予測モデルや異常検知モデルとしてアプリケーションとしても使うことができるという形になっているという理解の仕方ができると思います。
一方で、機械学習では予測、分類などを行うアプリケーションを作成するという意識を強く持っているという理解の仕方ができます。このため精度向上の優先度が高いのですが、一般論として複雑な現象をうまく表現するためには複雑な構造が必要で、トレードオフとしてモデル構造の解釈性が犠牲になりがちです。
統計解析の使いどころ
統計解析と機械学習の使い分け
機械学習と統計解析の使い分け方を考えてみましょう。 まず少量のデータしか使えないような状況では統計解析的なアプローチを取らざるを得ないでしょう。 次に、アドホックな分析や人間の判断を待ってから処理するようなシステムなどで、モデルの構造を人間が理解したいという要請がある場合にはやはり統計解析的なアプローチの優先度が高いと思います（ただしこの場合は機械学習的アプローチの精度と解釈性を比較して検討することになりそうです）。 途中で人間の介入が小さい自動化・システム化された運用を想定するのであれば、機械学習的アプローチでできる限り精度を上げる方向で検討するべきです（精度確保のために学習データは大量に準備したいですね）。
データ量が多いと統計解析は役に立たない？
昨今ではデータを全量蓄積するのは当たり前で、ほとんど母集団そのものと考えても良いようなデータを分析に活用できるケースも多くなってきました。 データ量が十分に大きければバラつきは無視できるほど小さくなるので、統計的な手法を用いて誤差や信頼区間を評価するまでもなく、機械学習的なアプローチで統計量や推定値そのものを計算するだけで済むようになってしまいます。 ビッグデータブームを経た現在に統計解析は不要になったと考えて良いのでしょうか。
実際にデータ分析をやってみると、単純に全体の傾向が知りたいというケースは少なく、特定のサブグループに注目して傾向を分析したり施策を検討したりするケースが非常に多いです（究極的には One to One マーケティングのような形になりがちです）。 データ件数が増えただけではなく、データ1件当たりの情報も詳しく取れるようになった結果として、より細かい分析ができる（したい）状況が生まれたわけです。サブグループを細かくしていくとバラつきがどの程度あるのかという議論が改めて発生します。また、目の前の現象が偶然かそうでないのか、という議論も統計解析ならば扱うことができます。
昨今では機械学習との垣根が低くなり同じようなことが機械学習的にできるようになってきましたが、統計解析的な手法でバラつきを推定したいケースもまだまだたくさんあります。状況に応じて使えるということが重要なのではないかと考えています。
おわりに
NTTデータ数理システムでは、統計解析、機械学習などの学問的な分類にはあまりこだわらず、お客様の現在の課題にどのようなアプローチが適しているかという観点で分析のアプローチをご提案します。当社にはビジネスの現場でどちらの技術も生かすことのできる技術者が多数在籍しています。データ分析、データ分析に関わるシステムの開発、データサイエンス教育など、様々な形でご支援が可能ですので、ぜひお気軽にご相談ください。
