- HOME
- psim言語講座(第3回)待ち行列 M/M/1 シミュレーションを拡張してみる

更新日:2025年2月12日 18:14
公開日:2021年8月24日 17:45
記事一覧
- psim言語講座(第1回)離散イベントシミュレーション(待ち行列 M/M/1モデル)を書いてみる
- psim言語講座(第2回)離散イベントシミュレーション(待ち行列 M/M/1モデル)を読んでみる
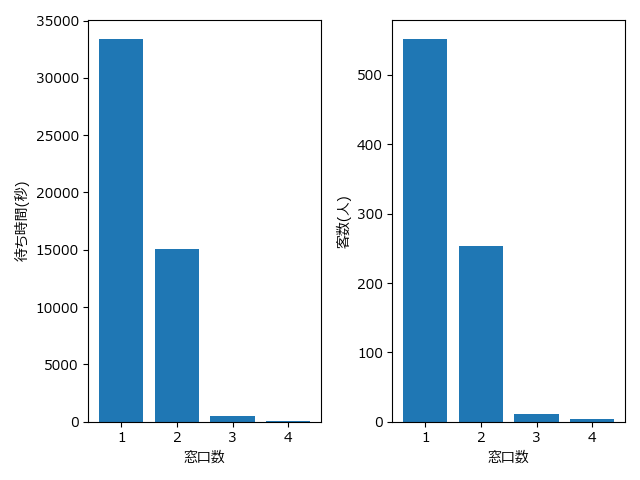
- psim言語講座(第3回)待ち行列 M/M/1 シミュレーションを拡張してみる
- psim言語講座(第4回)生産ラインシミュレーションを書いてみる
- psim言語講座(第5回)psimとexcelを連携してみる
- psim言語講座(第6回)psimとexcelを連携してみる(グラフ編)
- psim言語講座(第7回)連続型シミュレーションを書いてみる
- psim言語講座(第8回)エージェントシミュレーションを書いてみる
- psim言語講座(第9回)エージェントシミュレーションを拡張してみる
- psim言語講座(第10回)チュートリアル編(1)psim で 「Hello World!」
- psim言語講座(第11回)チュートリアル編(2)psim のプロセスを使いこなす
- psim言語講座(第12回)チュートリアル編(3)psim のファシリティを使いこなす
- psim言語講座(第13回)チュートリアル編(4)psim のストアを使いこなす
- psim言語講座(第14回)チュートリアル編(5)psim のスケジューラを使いこなす
- psim言語講座(第15回)チュートリアル編(6)(続)psim のストアを使いこなす
- psim言語講座(第16回)チュートリアル編(7)(続)psim のストアを使いこなす
- psim言語講座(第17回)チュートリアル編(8) AGV による搬送
- psim言語講座(第18回)チュートリアル編(9) 動的スケジューリング方式
- psim言語講座(第19回)チュートリアル編(10) 強化学習AGV方式