psim言語講座（第11回）チュートリアル編（2）

HOME
psim言語講座（第11回）チュートリアル編（2）

2023年7月18日 15:46

本記事は当社が発行しているシミュレーションメールマガジンVol.11の記事です。
シミュレーションメールマガジンの詳細・購読申込はこちらのサポートページから

はじめに

前回は、プロセスの定義方法を説明しました。

今回は、複数のプロセスが並行に走るような例を説明していきます。

並行プロセス

以下のコードは、2 つのプロセスA とプロセスBを定義し、並行に起動しています。

例えば、2 人の作業者に、それぞれ別の仕事を与え、それぞれが独立に作業を進めるようなモデルです。

initialize()
setGlobalSeed(0)

from psim import *

initialize()

def procA():
    g = exponentialDistribution(10)
    for i in range(5):
        yield pause(next(g))
        print(f"プロセスA 進捗{i+1}/6 時間 {now()}")

def procB():
    g = exponentialDistribution(9)
    for i in range(5):
        yield pause(next(g))
        print(f"プロセスB 進捗{i+1}/5 時間 {now()}")

activate(procA)()
activate(procB)()

start()

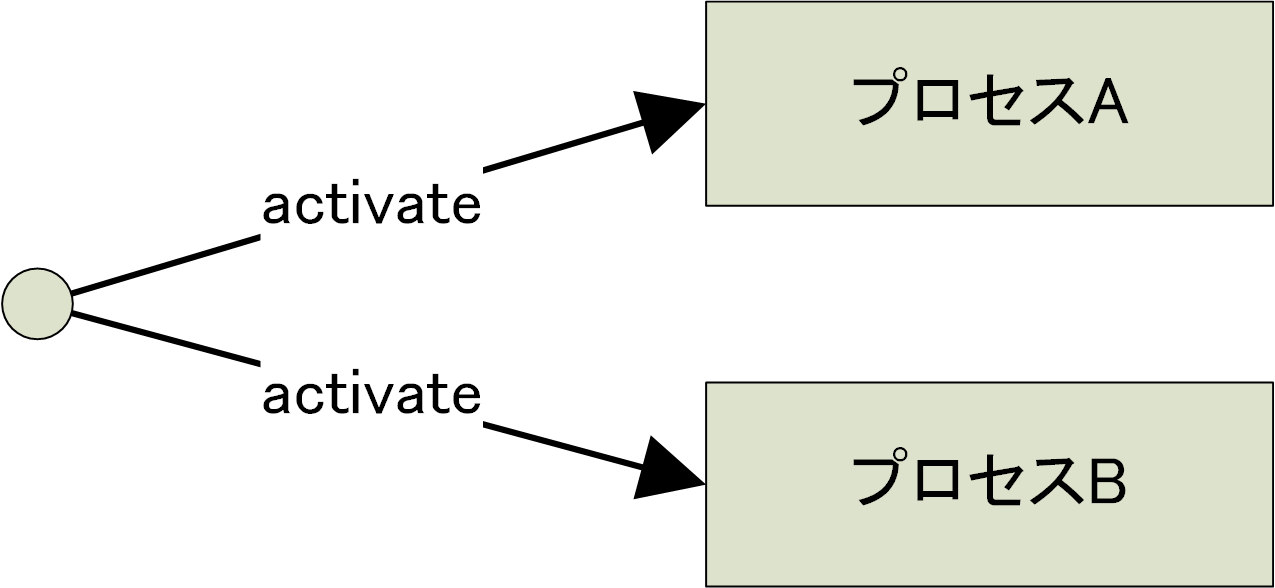
個々のプロセスは、前回のプロセスの定義方法に従って定義しています。それらを、activate すると、それらのプロセスは並列に起動します。

この例では、それぞれのプロセスは、進捗速度が少々異なり、内部で進捗状況を 5 回出力しています。

2つのプロセスが並列に起動するので、出力は以下のようになります。

プロセスA 進捗1/6 時間 7.9587450816311005
プロセスB 進捗1/5 時間 11.30337686669254
プロセスA 進捗2/6 時間 17.190976539671787
プロセスB 進捗2/5 時間 18.388187237547974
プロセスA 進捗3/6 時間 22.70146145062678
プロセスB 進捗3/5 時間 27.73162089204046
プロセスA 進捗4/6 時間 28.45665344231318
プロセスB 進捗4/5 時間 47.74334060933437
プロセスB 進捗5/5 時間 52.095759517454646
プロセスA 進捗5/6 時間 61.605775262851324

プロセスの引数

先の 2 つの並列プロセスは、ほぼ似たような定義です。

違いは、プロセス名と、平均作業時間のみです。

そのようなケースでは、以下のようにプロセスの定義に引数を使う事ができます。

initialize()
setGlobalSeed(0)

def proc(name, mean):
    # name: プロセス名
    # mean: 平均作業時間
    g = exponentialDistribution(mean)
    for i in range(5):
        yield pause(next(g))
        print(f"プロセス{name} 進捗{i+1}/5 時間 {now()}")

activate(proc)("A", 10)
activate(proc)("B", 9)

start()

この例では、setGlobalSeed(0) を実行しているので、乱数の種が共通であるので、結果は完全に一致します。

プロセスA 進捗1/6 時間 7.9587450816311005
プロセスB 進捗1/5 時間 11.30337686669254
プロセスA 進捗2/6 時間 17.190976539671787
プロセスB 進捗2/5 時間 18.388187237547974
プロセスA 進捗3/6 時間 22.70146145062678
プロセスB 進捗3/5 時間 27.73162089204046
プロセスA 進捗4/6 時間 28.45665344231318
プロセスB 進捗4/5 時間 47.74334060933437
プロセスB 進捗5/5 時間 52.095759517454646
プロセスA 進捗5/6 時間 61.605775262851324

状態遷移の記述

世の中の離散事象をモデリングすると、状態遷移を使って表現されるものが多いです。

例えば、工場の生産ラインなども状態遷移で表されます。

工程 G1, G2, G3 があり、その順番で状態遷移し、その後また、G1 に戻るような状態遷移を考えます。

そのような状態遷移モデルは以下のように yield go を使ってモデリングできます。

initialize()
setGlobalSeed(0)

g1 = exponentialDistribution(5)
def procG1():
    yield pause(next(g1))
    print(f"工程 G1 時間 {now()}")
    yield go(procG2)()

g2 = exponentialDistribution(7)
def procG2():
    yield pause(next(g2))
    print(f"工程 G2 時間 {now()}")
    yield go(procG3)()

g3 = exponentialDistribution(3)
def procG3():
    yield pause(next(g3))
    print(f"工程 G3 時間 {now()}")
    yield go(procG1)()

activate(procG1)()

start(until = 40)

yield go(プロセス名)(引数1, 引数2, ...)

は、現在のプロセスを、指定されたプロセス名に置き換えます。その際、呼出されるプロセスには、引数1, 引数2, ...が渡されます。

この例では、一方通行の状態遷移ですが、一般的なモデルでは、条件によって、遷移するプロセスが変化する事が多いです。

現実世界では、この「条件」はより複雑な待ち受けになる事が多く、そこが離散イベントシミュレーションの本質なのですが、ここでは、その説明は割愛します。

このシミュレーション実行結果は以下のようになります。

工程 G1 時間 3.9793725408155503
工程 G2 時間 12.770887881576416
工程 G3 時間 15.540557318988622
工程 G1 時間 19.476563080574977
工程 G2 時間 23.33390251824347
工程 G3 時間 26.448380403074296
工程 G1 時間 29.325976398917494

同期型のサブプロセス

一般的にプロセスには入れ子構造がよく現れます。

例えば、ある生産ラインの工程のひとつを分解すると、

製品をラインからピッキングする
加工する
製品をラインに戻す

と分解できるかもしれません。それぞれのサブ工程もプロセスです。更に、「加工する」工程の中を更に細分化できる事があります。

先程の工程 G1, G2, G3 があるような状態遷移のような工程を考えます。そして、G2 の内部で、サブ工程を呼出すようなモデルを考えます。

以下のコードは、上記のような工程を表現しています。

initialize()

g1 = exponentialDistribution(5)
def procG1():
    yield pause(next(g1))
    print(f"工程 G1 時間 {now()}")
    yield go(procG2)()

g2 = exponentialDistribution(7)
def procG2():
    yield pause(next(g2))
    print(f"工程 G2 時間 {now()}")
    yield call(subproc1)()
    yield go(procG3)()

sg1 = exponentialDistribution(3)
def subproc1():
    yield pause(next(sg1))
    print(f"   サブ工程1 時間 {now()}")
    yield go(subproc2)()

sg2 = exponentialDistribution(3)
def subproc2():
    yield pause(next(sg1))
    print(f"   サブ工程2 時間 {now()}")

g3 = exponentialDistribution(3)
def procG3():
    yield pause(next(g3))
    print(f"工程 G3 時間 {now()}")
    yield go(procG1)()

activate(procG1)()

start(until = 50)

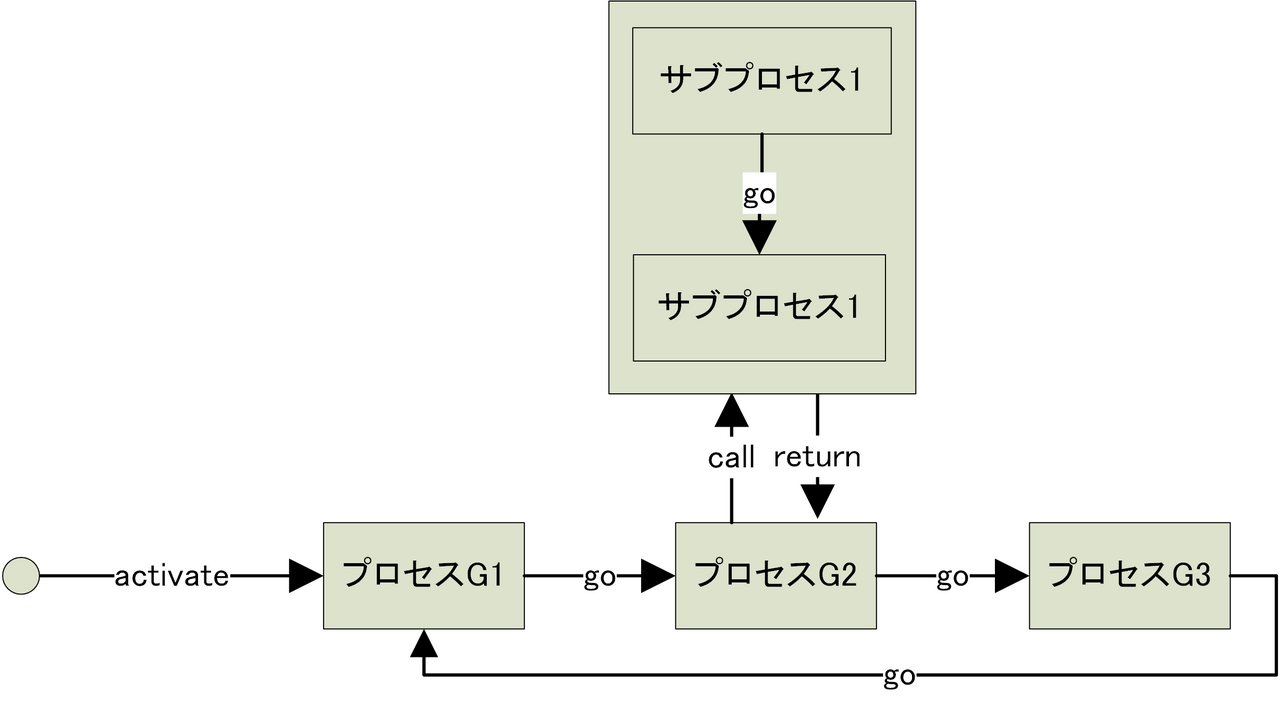
yield call(プロセス名)(引数1, 引数2, ...)

は、現在のプロセスを一時停止して、指定されたプロセス名を実行します。指定したプロセスが終了した、一時停止していたプロセスを再開します。

このシミュレーション実行結果は以下のようになります。

工程 G1 時間 7.844480699845842
工程 G2 時間 13.11319946660196
   サブ工程1 時間 15.631498006818429
   サブ工程2 時間 23.42626046859475
工程 G3 時間 23.647316533333296
工程 G1 時間 24.103121678928296
工程 G2 時間 24.24610078571787
   サブ工程1 時間 29.608563824562538
   サブ工程2 時間 34.125916520158185
工程 G3 時間 40.24685936299484
工程 H1 時間 3.9793725408155503

非同期型のサブプロセス

プロセスの入れ子構造は、同期的であるとは限りません。

例えば、生産ラインでは、複数の製品を搭載したパレットが流れてきたら、それらを分離して、別々のラインに流す事があります。

プロセスH1 は 3つの製品を搭載したパレットが流れてきたら、それらを分離して、別々のラインに流します。各ライン i は、H2工程と H3 工程を順番に通過します。

以下のコードは、上記のようなプロセスH1 を表現しています。

initialize()
setGlobalSeed(0)

g1 = exponentialDistribution(5)
def procH1():
    yield pause(next(g1))
    print(f"工程 H1 時間 {now()}")
    for i in range(3):
        yield subactivate(procH2)(i)
    yield alwaysFalse()

g2 = exponentialDistribution(7)
def procH2(i):
    yield pause(next(g2))
    print(f"ライン {i} 工程 H2 時間 {now()}")
    yield go(procH3)(i)

g3 = exponentialDistribution(3)
def procH3(i):
    yield pause(next(g3))
    print(f"ライン {i} 工程 H3 時間 {now()}")

activate(procH1)()

start()

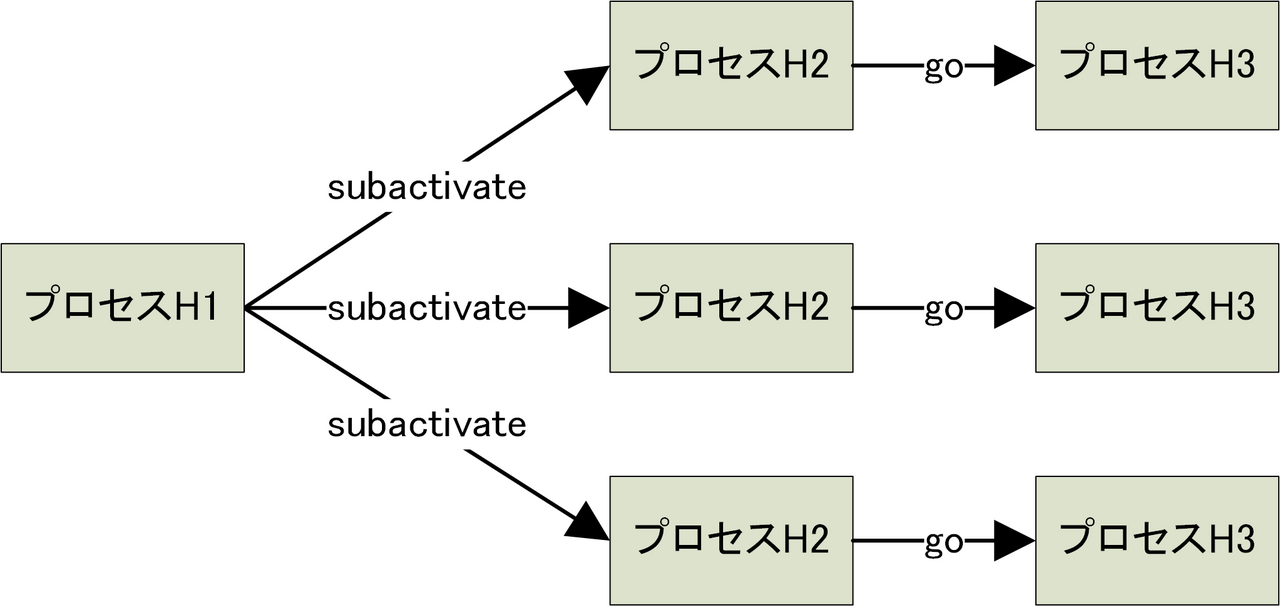
yield subactivate(プロセス名)(引数1, 引数2, ...)

は、指定されたプロセス名を非同期で実行します。

ただし、subactivate を呼出したプロセスが終了した場合、非同期で起動したサブプロセスも終了します。

今回の例では、非同期で起動したサブプロセスが親と連動して終了してしまうと困っていまうので、yield alwaysFalse() を呼出し、親プロセスの終了を抑制しています。

この例の場合は、yield subactivate ではなく、activate を呼出す方が適切です。activateで起動したサブプロセスは、生存時間に親子関係の依存は無くなります。

このシミュレーション実行結果は以下のようになります。

工程 H1 時間 3.9793725408155503
ライン 2 工程 H2 時間 9.489780607036446
ライン 1 工程 H2 時間 10.441934561444032
ライン 2 工程 H3 時間 11.142926080322944
ライン 0 工程 H2 時間 12.770887881576416
ライン 1 工程 H3 時間 13.55641244627486
ライン 0 工程 H3 時間 14.497445479082335