はじめに
前回の記事 で、Physics-informed Neural Network (PINN) を用いた逆問題 (=あらかじめ解についての情報が手元にある状況で、PDE や種々の条件を求める問題) の解法についてご紹介しました。今回の記事では、産業応用に近い逆問題の例として、光学メタマテリアルの設計を取り上げ、そこに物理法則を組み込んだ機械学習技術 (PIML) を応用する手法についてご紹介します。今回紹介する PIML は、PINN のように PDE を Neural Network の損失関数として解く方法ではなく、より広い、Physics と Machine Learning の融合した方法となります。
メタマテリアルとは[1]、自然界には存在しない人工的に構成された構造体で、そのマクロな性質が構成要素の材質そのものではなく、ミクロな構造配置に依存する材料です。特にナノフォトニクスの分野では、光の波長より小さなスケールで構造を設計することで、波動の伝播・反射・屈折などを精密に制御できるようになります[2]。これにより、たとえば、負の屈折率を持つレンズや、物体を不可視にする「メタサーフェス型のステルス構造」[3]など、従来の材料では不可能だった物理的振る舞いを実現できる点が特徴です。このように、メタマテリアルはその非直感的な物理的特性により、光学、電磁気学、音響工学などの分野で革新的な応用が期待されています。
メタマテリアルの設計では、材料のミクロな構造を設計する=所望の性能を満たすようなミクロな構造を求める必要があります。ミクロな構造であるために、設計空間は高次元になります。また、目的関数が非線形で、かつ制約条件が多いこともあり、従来の有限要素法(FEM)などの数値解析手法では得られる設計の性能や計算時間に限界が生じます。
こうした課題に対して、物理法則を組み込んだ機械学習技術 (PIML) は優れた能力を発揮します。例えば計算時間について、従来の手法では、設計空間が広いために何度も数値解析を行う必要があり、非常に計算コストが高くなります。しかし、PIMLでは、物理法則を組み込みながら効率的に逆問題を解くことができ、従来のアプローチに比べて計算資源を節約しつつ有用な解を得ることが可能です。また、設計問題に応じて、ニューラルネットワークのアーキテクチャや目的関数を適切に選択することで、様々な設計問題に対応できる柔軟性も備えています。
本記事ではまず、メタマテリアル設計への PIML の応用 の節で、PIML を用いてメタマテリアルの設計問題を解く方法について解説します。次に、最適設計を PIML で行う方法 の節で、生成モデルを用いた方法を紹介します。最後に、実験:メタサーフェスの設計 の節で、メタマテリアルの設計を行った実験結果をご紹介します。
- はじめに
- メタマテリアル設計への PIML の応用
- 数値シミュレーションを PIML で行う方法
- 最適設計を PIML で行う方法
- 数値シミュレーションと最適設計を両方 PIML で行う方法
- 最適設計を PIML で行う方法
- 実験:メタサーフェスの設計
- おわりに
メタマテリアル設計への PIML の応用
本節では、メタマテリアルデザイン、特にナノフォトニクス分野での光学メタマテリアルの設計に PIML を用いる手法について解説します。メタマテリアルの設計は一般的に、以下の手続き 1, 2 を交互に繰り返すことで行われます [4]。
- (数値シミュレーション) 現状の設計に対して、シミュレーターを用いて光学応答をシミュレートし、現状の設計の性能指標 (Figure of Merit, FoM) を算出する。
- (最適設計) FoM が増加するように、現状の設計を修正して新たな設計を生成する。
数値シミュレーションのコストは高く、また、設計空間が高次元で非線形かつ制約条件が多い場合、既存の数値シミュレーションの手法を用いた従来手法では限界が生じます。
そこで、上記の設計プロセスに PIML を取り入れるアプローチとして、以下の 3 つの方法が盛んに研究されています。
- 数値シミュレーションの部分を PIML で行う方法 [5]
- 最適設計の部分を PIML で行う方法 [6]
- 数値シミュレーションと最適設計を両方 PIML で行う方法 [7]
以下では、それぞれの方法のアイデアについてご紹介します。
前回ご紹介した PINN で逆問題を解く方法 [8] は、1,2, を交互に繰り返す方法ではなく、ニューラルネットワークの学習を用いて 1, 2 を同時に実行する方法でした。しかし、最適化すべきパラメータが高次元になると、それも難しくなります。
数値シミュレーションを PIML で行う方法
通常、光学応答の数値シミュレーションには、メタマテリアルの構造と入射光のパラメータ(波長や偏光など)から、有限要素法などに基づくマクスウェル方程式のソルバーを用い、光学応答をシミュレートします。本節の方法では、この数値シミュレーションの部分をニューラルネットワークによる代理モデル (surrogate model) で代用し、計算を簡略化します。具体的には、以下の 2 段階のプロセス (Fig.1) で設計を行うことになります。
代理モデルの事前学習:代理モデルとは、メタマテリアルの構造と入射光のパラメータを入力とし、光学応答を出力とするニューラルネットワークのことです。最適設計を行う前に、様々な構造や入射光のパラメータに対する光学応答を学習させることで、代理モデルの作成を予め行っておきます。
代理モデルを用いた最適設計:通常のマクスウェル方程式のソルバーの代わりに、代理モデルによる推論を用いて、光学応答の予測を行います。光学応答から算出した性能指標が増加するように、現状の設計を修正して新たな設計を生成します。
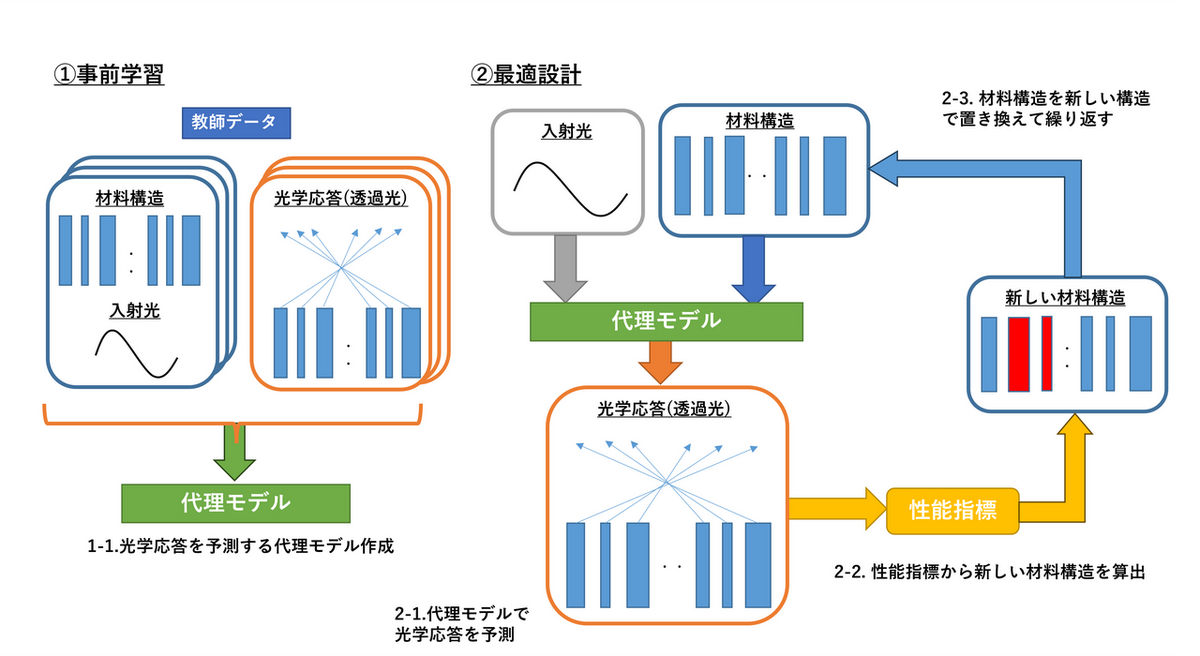 Fig.1 数値シミュレーションを PIML で行う方法
Fig.1 数値シミュレーションを PIML で行う方法
このアプローチには以下のメリットがあります。
- いったん代理モデルの学習が済んでいれば、ニューラルネットワークによる光学応答の予測=数値シミュレーション、は極めて高速に行えるため、数値シミュレーション部分にかかる計算時間を大幅に短縮できる。
- ニューラルネットワークでは、入力に対する出力の微分が自動微分で計算できるため、性能指標を増加させるような設計の変化方向 (勾配ベクトル) が容易に計算でき、最適設計の際に利用することができる。
一方、以下のようなデメリットがあります。
- ニューラルネットワークの事前学習に必要な教師データの生成や、学習自体に多くの時間がかかり、上記の計算時間短縮のメリットを打ち消してしまう可能性がある
- ニューラルネットワークの予測精度がある程度高くないと、最終的な設計も的外れとなる
文献 [8] では、上記のデメリットに対処する (少ない教師データまたは教師データなしでも高性能なモデルを作成する) ために、損失関数として、マクスウェル方程式を満たさないことに対する罰則 (physics-informed loss) を用いて代理モデルの学習を行っています。
最適設計を PIML で行う方法
このアプローチでは、設計変数の生成に GAN などの生成ニューラルネットワークを活用します。メタマテリアルの設計において、設計の自由度のベクトルを $x$ とすると、性能指標 (FoM) による設計の条件づき分布 $p(x|FoM)$ を求められれば、所望の性質を持つ設計が求められます。メタマテリアルは光の波長より小さい微細な構造の集積のため、$x$ は極めて高次元のベクトルとなります。このアプローチでは、高次元の空間の条件付き分布 $p(x|FoM)$ を、生成ニューラルネットワークで学習します (Fig.2)。
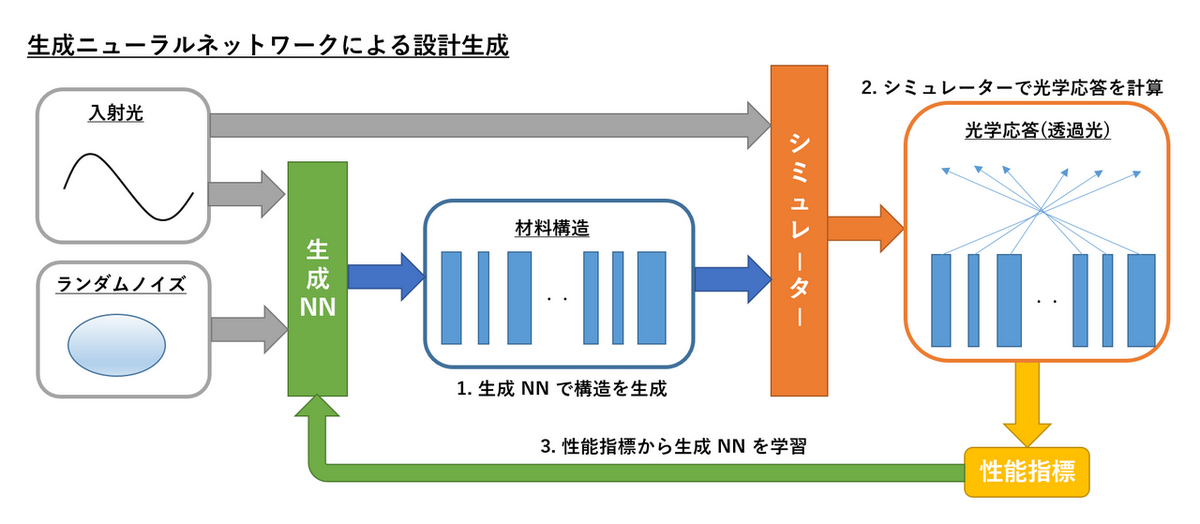 Fig.2 最適設計を PIML で行う方法
Fig.2 最適設計を PIML で行う方法
このアプローチには以下のメリットがあります。
- 通常のメタマテリアルの設計手法では、設計の自由度が大きい場合に、初期設計の近傍しか探索できず、性能指標が大きい設計が得られるか否かが、初期設計に依存するという問題がありました。生成ニューラルネットワークを使うことで、高次元の空間の条件付き分布 $p(x|FoM)$ を効率的に学習し、上記の初期設計依存性を回避することができます [6]。
一方、以下のようなデメリットがあります。
- 設計変数の評価のためには数値シミュレーションが必要になります。そのため、評価回数が多いと計算時間がかかります。
- ニューラルネットワークを用いた生成モデルの学習は、ハイパーパラメータの慎重な調整が必要で難易度が高いことが知られています。
数値シミュレーションと最適生成を両方 PIML で行う方法
数値シミュレーションと設計生成の両方に PIML を用いるアプローチも検討されています。文献 [7] では、マクスウェル方程式の代理モデルを数値シミュレーション部分に用いて、設計生成を行う生成モデルを学習 (最適化) します。数値シミュレーションに代理モデルを用いることで、前節の計算時間のデメリットを緩和するとともに、生成モデルを用いることで複雑な設計空間の分布を学習しています。
最適設計を PIML で行う方法
本節では、2. の最適設計モデルについて、文献 [6] で提案された内容を参考にしてご紹介します。
モデル
乱数ベクトル $z$ を入力とし、 ${n_i}_{i=1}^{N} \in [-1, 1]^N$ を出力とする生成ニューラルネットワークを用意します。$n_i$ は $i$ 番目の位置に材料があるか (1)、ないか (-1) を表すベクトル (設計ベクトル) です。 ただし、ニューラルネットワークで扱えるように、値を $[-1, 1]$ に連続化しています。
損失関数
上記のニューラルネットワークが性能指標の高い設計ベクトルのみを出力するように学習を行います。学習の損失関数としては以下の式を用います。
[[
\mathcal L = - \frac1M \sum_{m=1}^M FoM^{(m)} + \frac{\beta}M \sum_{m=1}^M |n^{(m)}|\cdot|2-n^{(m)}| .
]]
ただし、$M$ はバッチサイズ、$n^{(m)}$、$FoM^{(m)}$ はバッチの $m$ 番目の設計の設計ベクトルおよび FoM の値です。第一項によって、学習が進むとモデルが FoM の大きい設計のみを生成するようになります。第二項は、$n^{(m)}_i \in [-1, 1]$ を -1 または 1 へと誘導する正則化項です。
学習方法
上記の $\mathcal L$ を用いてニューラルネットワークの学習を行うためには、損失 $\mathcal L$ のニューラルネットワークのパラメータ $\theta$ に対する勾配を計算する必要があります。チェインルールを用いると勾配は以下のように分解できます。
[[
\frac{\partial \mathcal L}{\partial \theta} = \frac{\partial \mathcal L}{\partial n}\frac{\partial n}{\partial \theta}
]]
ここで、第一項の $\frac{\partial \mathcal L}{\partial n}$ は設計を変えると性能指標がどの程度変わるかを表す勾配です。この勾配は、論文 [6] のように adjoint 法により求めることもできますし、FoM を求める数値シミュレーションの際のソルバーとして、微分可能なソルバー [9] を用いれば、自動微分によって end-to-end に算出することも可能です。第二項の勾配 $\frac{\partial n}{\partial \theta}$ は、ニューラルネットワークの出力のパラメータ $\theta$ に対する勾配です。
実験:メタサーフェスの設計
メタサーフェスとは、入射光を所望の角度に回折させる平面状の構造物です。本節では、メタサーフェスの設計において、文献 [6] と同じ問題設定で実験を行った結果を紹介します。
設計対象
今回の実験では、z=0 の xy 平面に置かれたメタサーフェスの構造の設計を行います。メタサーフェスは、二酸化ケイ素の基盤の上に、x 軸方向に周期的な構造を繰り返して出来ています。各周期構造は x 軸方向に $N=256$ 個のセグメントから出来ており、各セグメントの上には、厚さ 325 nm のシリコンが載っているか、何も載っていないかのどちらかです (Fig.3 参照)。
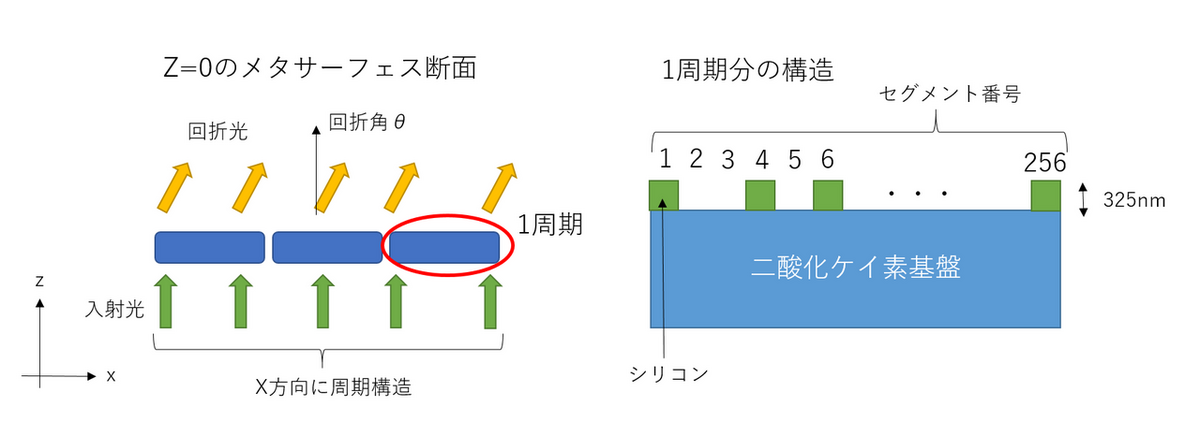 Fig.3 メタサーフェス
Fig.3 メタサーフェス
学習設定
学習の際の設定は以下の通りです。
| 変数 |
値 |
| 設計変数 |
各セグメント上のシリコンの有無を表す2値変数 $\{n_i\}_{i=1}^{N} \in \{-1, 1\}^N$ |
| 入射光の波長、偏光 |
900nm, TM 偏光 |
| 目標回折角 |
60° |
| オプティマイザ |
Adam |
| 学習率 |
$0.001$ |
| バッチサイズ |
50 |
| iter数 |
3000 |
| アーキテクチャ |
1d DCGAN (深さ4) |
| $\beta$ |
1.25 if iter > 400 else 0 |
結果
学習済みのモデルを用いて、100 個の設計を生成した場合の性能指標の分布は Fig.5 の通りとなり、平均 FoM は 86% となりました。比較のために、100 個のランダムな初期設計から adjoint 法で最適化を行ったそれぞれの FoM の分布もプロットしています。
今回の実験設定では、 本手法は良い初期値を使わない adjoint 法よりも高い性能指標の設計を見つけられています。
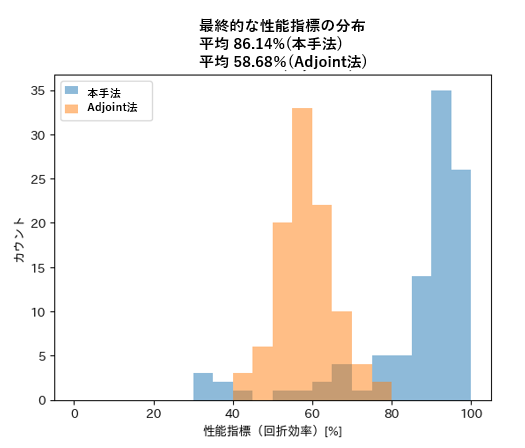 Fig.4 FoM 分布
Fig.4 FoM 分布
本手法で設計の最適化の様子を可視化したものが以下のグラフです。
表の一行目では、学習とともに生成される設計がどのように変化するかを調べました。グラフの横軸と縦軸は、設計ベクトルの第一主成分と第荷主成分を表し、各点がニューラルネットワークの出力した一つ一つの設計ベクトルに対応しており、性能指標の値によって色づけています。学習していない段階では、設計ベクトルが散らばっていますが、学習が進むにつれて、設計ベクトルが性能指標の高い幾つかの設計に集中していくことがわかります。
表の二行目では、学習とともに生成される設計の性能指標の分布がどのように変化するかを調べました。学習が進むにつれて、性能指標が高い設計が出力されてゆく様子がわかります。
|
0 iter |
1000 iter |
2000 iter |
| 設計ベクトルの分布 |
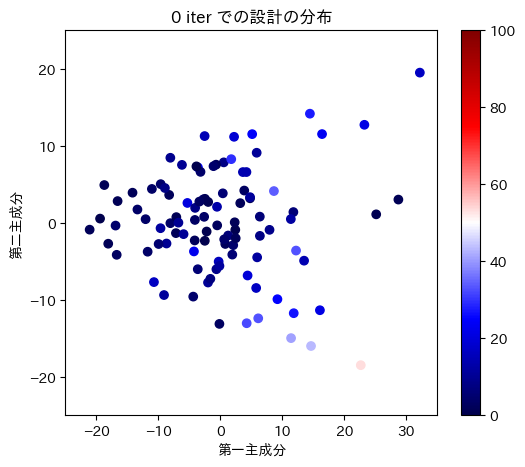 |
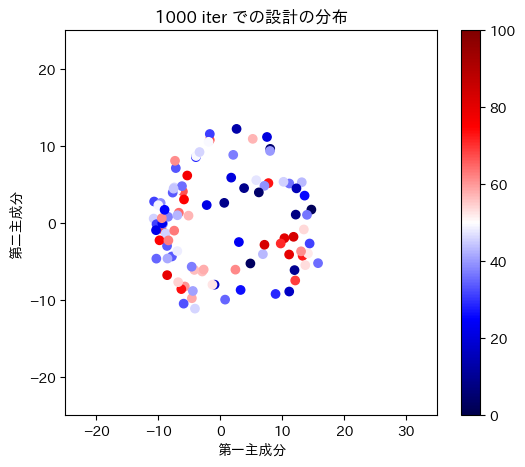 |
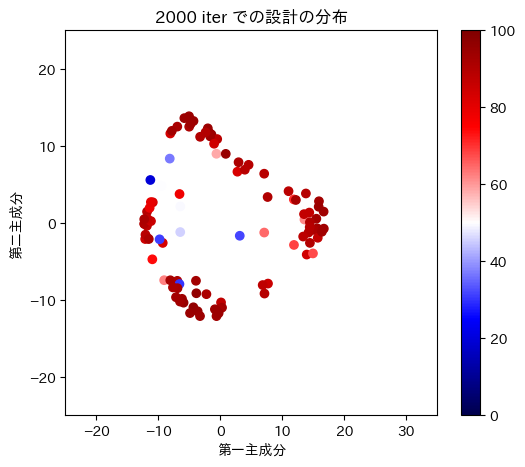 |
| 性能指標の分布 |
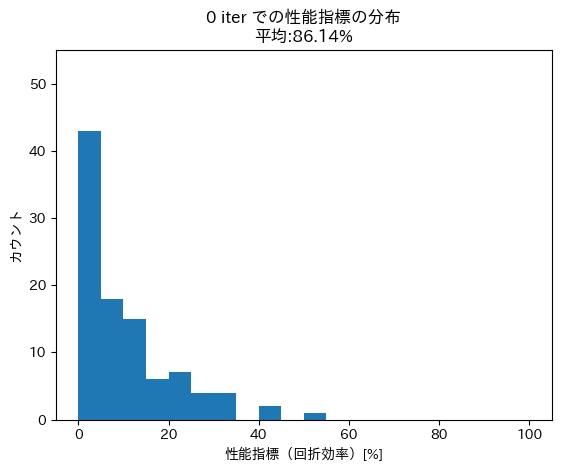 |
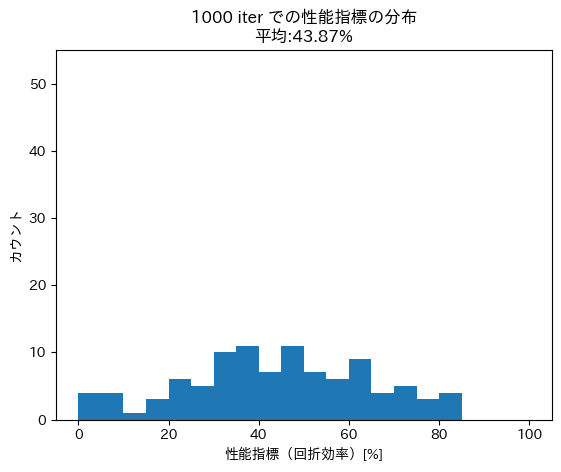 |
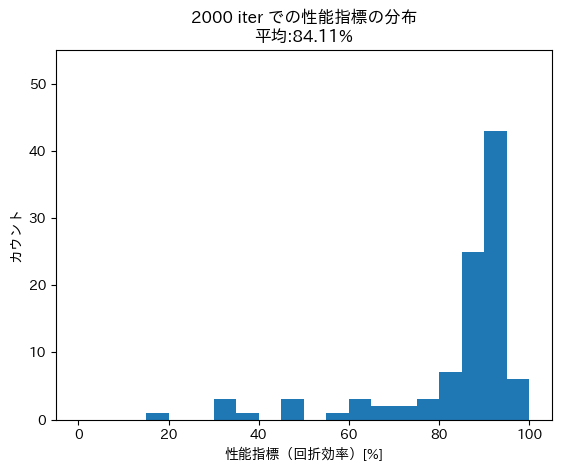 |
Fig.5 最適化の可視化の様子
おわりに
本記事では、光学メタマテリアルの設計に PIML を応用する手法として、文献 [6] を参考に、最適設計を生成ニューラルネットワークで行う方法をご紹介しました。実際にメタサーフェスの設計を行い、その結果をご紹介しました。生成ニューラルネットワークによる方法は、設計空間の再パラメータ化、もしくは Hypernetwork [10] と見なすことが出来ます。設計空間は膨大な可能性(今回の場合は $2^{256}$)がありますが、所望の結果を得るパターンはそのうちの一部です。実際の設計は、可能なパターンに比べると非常に少数であることから、低次元多様体仮説が成立していると考えることが出来、Hypernetwork はそれを学習していると考えることが出来ます。実際、Fig.4 を見ると、設計空間内の一部の領域を学習できていることがわかります。
PIML を用いたメタマテリアルの設計は、まだ研究段階の技術です。生成ニューラルネットワークによる設計の多様性を担保するためには、生成されるデータが設計空間全体をカバーする必要があり、以下のような方向性が示されています。
今後も研究がさらに進展し、将来的には、実用的な新しいメタマテリアルがこれらの手法を用いて発見されることが期待されています。
次回の記事では、PIML の PINN に並んで重要な例である Neural Operator (NO) についてご紹介します。
参考文献
雪島 正敏
株式会社NTTデータ数理システム
シミュレーション&マイニング部 部長
機械学習・シミュレーションなどの技術を活用したAI活用/データ分析の案件を年間70件以上こなすシミュレーション&マイニング部を牽引する。
常に最新技術を調査し、お客様からの様々な要件に対して最適な技術提案を行う。
清水 浩之
株式会社NTTデータ数理システム シミュレーション&マイニング部所属。
博士号(理学)取得後、当社に入社。現在は機械学習、統計解析を活用した企業や社会における課題解決に取り組んでいる。
技術調査、データ分析、モデル開発、システムへの実装といった業務を手掛ける。
趣味:旅行、歴史、美術鑑賞

























