S4 で始める強化学習（第3回）離散イベントシミュレーションで理解を深める

本記事は当社が発行しているシミュレーションメールマガジンVol. 8の記事です。 シミュレーションメールマガジンの詳細・購読申込はこちら のサポートページから

はじめに

S⁴ で強化学習を使ったシミュレーションモデルを作成してみようという講座の3回目の記事になります。

1回目、2回目の記事で、離散イベントシミュレーションで強化学習を使うミニマルなモデルとして「窓口の割り当て問題」を紹介し、S⁴ で作成・実行する様子をお見せしました。

シミュレーションの醍醐味に、一度作成したモデルのパラメータを様々に変更して結果を比較できるという点があります。今回は強化学習モデルの主なパラメータを紹介し、それらを変更して実験することで強化学習について理解を深めたいと思います。

Q学習について

これまでに作成した強化学習モデルは、デフォルトの「Q学習」を学習手法として用いていました。Q学習には主なパラメータとして、割引率 $\gamma$、学習率 $\alpha$、そして $\varepsilon$ があり、それぞれ0以上1以下の値を取ります。ちょうど良いタイミングなので、Q学習の解説も兼ねながらそれぞれの意味を簡単に解説します。

まず割引率と学習率は、2回目の記事で紹介した行動価値関数の更新に関係するパラメータです（2回目の記事の図を参照していただくと以下わかりやすいかもしれません）。時刻 $t$ における窓口1、2の行列の長さをそれぞれ $n_{1t}$、$n_{2t}$、どちらの窓口に案内するかの行動を $a_t$ 、即時報酬を $r_t$ （これは $-(n_{1t} + n_{2t})$ と設定したのでした）と書くことにします。ここで簡単のため $(n_{1t}, n_{2t})$ の組を状態 $s_t$ と書き表すことにすると、行動価値関数は $Q(s, a)$ と書くことができます[1]。エージェントは時刻 $t$ に $s_t$ を観測したとき、行動価値関数をもとに、基本的に $Q(s_t, a)$ の値が最大になるような行動 $a$ を $a_t$ として選択します。

状態、行動、即時報酬が $s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1}, r_{t+2}, ...$ という順番で決定されるとしたとき[2]、状態 $s_{t+1}$ が判明する度に、Q学習では行動価値関数は次の式にしたがって更新されます:

[[ Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha(r_{t+1} + \gamma \max_{a} Q(s_{t+1}, a) - Q(s_t, a_t)) . ]]

簡単に言えば $Q(s_t, a_t)$ を $\displaystyle r_{t+1} + \gamma \max_{a} Q(s_{t+1}, a)$ の方向に更新していくということです。例えば $\alpha = 1$、$\gamma = 0$ の場合は意味がわかりやすく、上の更新式は $Q(s_t, a_t) \leftarrow r_{t+1}$ つまり即時報酬そのものを行動価値関数の値にするという意味になります。それ以外のとき、それぞれのパラメータの意味は以下の通りになります。

• 割引率 $\gamma$ が正のとき、行動価値関数はより長期的な報酬を表すようになります。$\displaystyle\max_{a} Q(s_{t+1}, a)$ は次の時刻において最適な行動をとったときの行動価値関数の値なので、$\displaystyle r_{t+1} + \gamma \max_{a} Q(s_{t+1}, a)$ は短期的な即時報酬 $r_{t+1}$ だけではなく、より報酬の見込める状態 $s_{t+1}$ に移れるかも加味しているからです。実際、行動価値関数は更新を繰り返すと、即時報酬の割引付きの総和 $G_t := r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + ...$ の期待値を見積もった値になります。
• 学習率 $\alpha$ が1以下のとき、行動価値関数を徐々に更新します。更新式は重み付きの現在の値 $(1-\alpha) Q(s_t, a_t)$ と新しい値 $\displaystyle\alpha(r_{t+1} + \gamma \max_{a} Q(s_{t+1}, a))$ の和に書き換えられるので、$\alpha$ は新しい値をどれくらいの割合で取り入れるかという意味になります。

最後に $\varepsilon$ は行動の選択に関するパラメータです。先ほど基本的に $Q(s_t, a)$ の値が最大になるような行動 $a$ を選択すると言いましたが、実際には $\varepsilon$ の確率で行動 $a$ を一様ランダムに選択し、残りの $1-\varepsilon$ の確率で $Q(s_t, a)$ の値が最大になるような行動 $a$ を選択します。正の $\varepsilon$ を設定することで、行動価値関数の更新が特定の状態、行動ペアに偏らないようにする狙いがあります。このような選択方法を$\varepsilon$-greedy法と言います。正確には$\varepsilon$-greedy法はQ学習の一部というわけではなく、他の方法をQ学習と組み合わせることもできます。

以上が、Q学習の概要です。かなり駆け足の説明ではありましたが、Q学習とそのパラメータについて雰囲気だけでも伝われば幸いです。

• $Q(s, a)$という表記は、第一引数を状態、第二引数を行動とする関数という意味です。一方、$Q(s_t, a_t)$と書いた場合はそれぞれの引数に$s_t$, $a_t$を代入したときの関数の値を表します。
• $r_t$, $s_t$, $a_t$ は一般的には確率変数として定式化されます。またこれら確率変数の遷移についてマルコフ決定過程という性質を仮定することが多いです。詳しくは他の文献を参照ください。

パラメータを変えて実験

それでは強化学習パラメータの値を変更して実験してみましょう。強化学習パラメータは、S⁴ のエディタ上「離散イベント用強化学習モデル」の編集画面から設定できます。

ここでは例として、学習率 $\alpha$ と $\varepsilon$ についてパラメータの値を少しずつ変更し平均通過時間（シミュレーション開始から終了までの積算）を比較します。各パラメータ値につき10回シミュレーションを行い、平均と標準偏差を求めた結果を次に示します[3]。

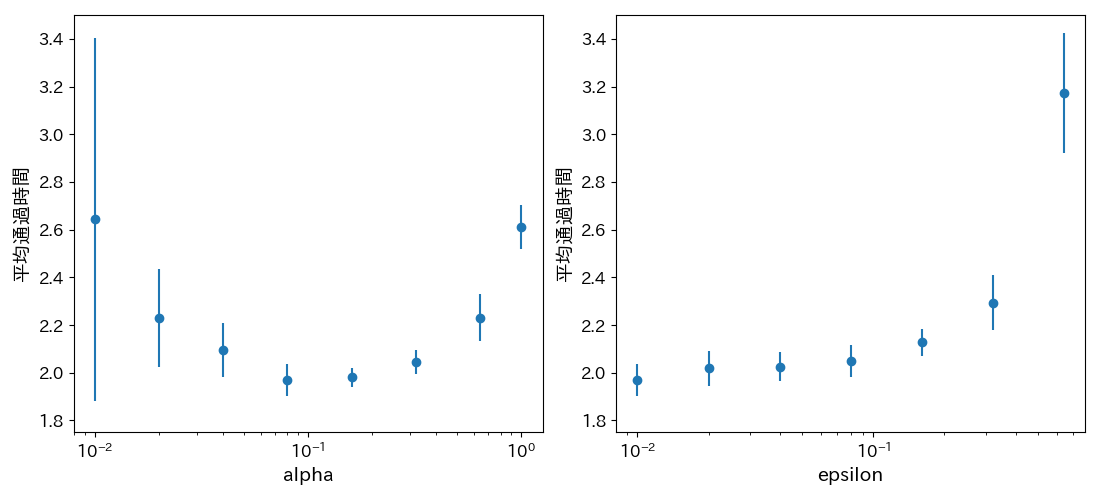
左の図は、他のパラメータはデフォルト値[4]のまま固定して学習率 $\alpha$ を0.01から1まで振った結果です。右の図は、$\alpha = 0.08$ としその他のパラメータはデフォルト値のまま固定して $\varepsilon$ を0.01から0.64まで振った結果です。

左の図を見ると、学習率が0と1の中間的な値のとき平均通過時間が最も短くなることがわかります。これは次のように理解することができます。学習率が小さいとき、行動価値関数の収束値の精度は高くなりますが、エージェントが適切な割り当てを行うような行動価値関数を得るまでに時間がかかり、それまで行列が発生してしまいます。一方で学習率が大きいとき、エージェントは早く適切な割り当てを行うようになりますが、行動価値関数の収束値の精度は低くなり判断の難しいケースで最適でない行動を取ってしまいます。つまり、早く適切な行動価値関数を得ることと、最終的に精度の高い行動価値関数を得ることの間にトレードオフの関係があり、その結果として $\alpha$ は中間的な値で最適になるということです。

一方で $\varepsilon$ については、小さければ小さいほど良いという結果になりました[5]。$\varepsilon$ の役割としては行動価値関数の更新が特定の状態、行動ペアに偏らないようにすることだと説明しましたが、今回の簡単な問題ではその必要はなかったようです。$\varepsilon$ の値が大きいとき、ランダムな割り当てを行う確率が大きくなるのでその分行列が長くなります。

割引率 $\gamma$ については解釈が難しかったため、今回は割愛することにしました。今回の簡単な問題では $\gamma$ の値によって獲得できる行動に差はないと考えられますが、手元で調べたところ学習の収束の早さや安定性に関係しているようでした。興味を持たれた方はぜひ実験していただけたらと思います。

• S⁴ で複数回シミュレーションを実行して統計量を調べるには、一括実行機能を使います。メニューから「パラメータを編集する」を開いて実行種類を一括実行にし、一括実行タブから出力としてself.getTimeMonitor(u"平均通過時間の記録-記録")[u"ave_time"][-1]を追加します。
• S⁴ におけるデフォルト値は $\alpha = 0.01$、$\gamma = 0.7$、$\varepsilon = 0.01$ です。
• 手元で $\varepsilon = 0$ の場合も確かめましたが、$1.98 \pm 0.07$ という結果が得られたので、$\varepsilon < 0.01$ ではほとんど値が変わらないと考えられます。

終わりに

今回までで離散イベントシミュレーションで強化学習を使う例について一通り解説しました。 次回は話題を変えて、エージェントシミュレーションで強化学習を使う例を扱いたいと思います。