S⁴ で始める強化学習（第7回）エージェントシミュレーションで理解を深める

本記事は当社が発行しているシミュレーションメールマガジンVol. 13の記事です。 シミュレーションメールマガジンの詳細・購読申込はこちらのサポートページから

はじめに

S⁴ で強化学習を使ったシミュレーションモデルを作成してみようという講座の7回目の記事になります。

4回目から6回目の記事で、エージェントシミュレーションで強化学習を使うモデルとして「崖歩き問題」を紹介し、S⁴ で作成・実行する方法を解説しました。

今回は、強化学習の理解を深めるための話題として、Actor-Criticという新しい学習方法を紹介し、Q学習との違いについて見ていきます。

Actor-Criticを使ってみる

Actor-Criticの詳細を解説する前に、まずはこれを使ったエージェントの学習を試してみましょう。これまでにお配りしているこちらのプロジェクトをもとに設定・実行する様子をお見せします。

エディタ上の「エージェント用強化学習モデル」をダブルクリックして開き、属性設定タブの下の方にある学習モデルという欄で「ActorCriticモデル」を選択します。Actor-Criticでは行動選択に$\varepsilon$-greedy法よりもソフトマックス法を使うことが多いので、方策という欄でSoftmaxを選択し、温度を10に設定します（これらの意味については後述します）。さらに下方にある即時報酬値の割引率を1に、学習率を0.1に、トレースの $\lambda$ を0に、Actorの学習率を0.1に設定します。そしたらOKボタンを押してモデルを開始してみてください。

モデルを開始すると、エージェントの行動がアニメーションとして確認できます。 行動の様子が確認できたらアニメーションを閉じて、最後までシミュレーションを実行してください。 シミュレーションの実行後、エピソードあたり報酬のプロットを確認してみましょう。

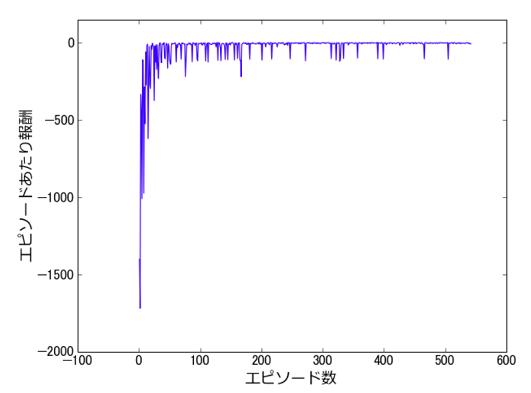
今回は $\varepsilon$-greedy法を用いていないので単純な比較は難しいですが、Q学習のときの結果（4回目の記事を参照）と比べて、0付近の報酬を獲得できるようになった後の報酬が安定し、下向きのスパイクの数が減っているように見えます。

次に、学習によって得られた行動ルールを確認してみましょう。Actor-Criticでは行動価値関数は登場しません。その代わりに状態価値関数と方策（policy）の2種類が登場します。ここではエージェントの行動ルールを意味する方策について確認してみましょう。

左のブラウザのワークスペースから、「崖歩き（強化学習）」プロジェクトの出力以下にある「エージェント用強化学習モデル - 学習モデル」を右クリックし「学習モデルを閲覧する」を選択します。設定タブから閲覧対象を「方策」として下の方の計算ボタンを押すと、方策を表すテーブルが表示されます。方策は状態（x, y座標）と行動に対して、その行動を取る確率を返す関数です。

今回もこれを可視化したいと思います。 結果タブ下の方の「モニタとして出力」ボタンを押して、モニタの名前を「方策」と設定します。 そしたら強化学習モデルビューアは閉じて、メインのエディタ上で右クリックを押し、分析スクリプトを開始するからvisPolicyを選択します。すると以下のようなプロットが表示されるかと思います。

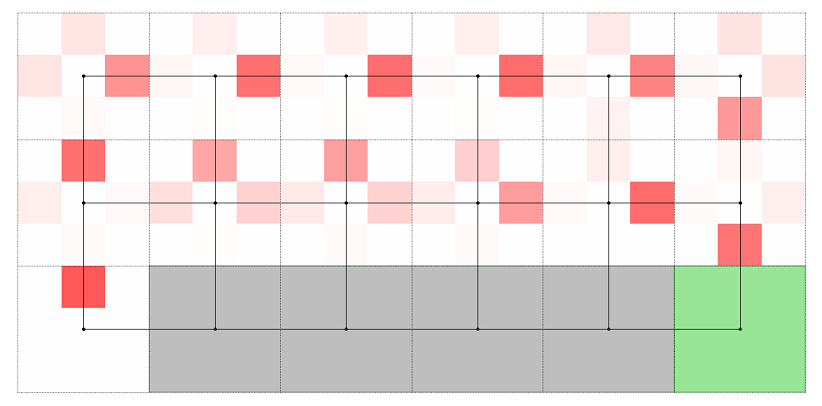
これは各マスにおける上下左右の行動の確率を色の濃淡で表したものです。Q学習のときと違い、崖から少し離れたマスを通ってゴールまで移動する行動を学習できていることが読み取れます。行動のバラつきを考慮すれば、Actor-Criticにより獲得される行動の方がより安全にゴールまで進むことができそうです。先ほどエピソードあたり報酬のプロットで、後半の下向きのスパイクの数が減っていると書きましたが、これは崖から距離を置いた方策のためと理解できます。

獲得される方策について、Q学習の場合との違いをどう理解すれば良いでしょうか。次の節で、Actor-Criticの学習方法と合わせて解説します。

Actor-Criticについて

Actor-Criticは、これまで利用していたQ学習から考え方を2段階変えたような学習手法です。ここではQ学習から始めて、段階を追ってActor-Criticを導く形で、Actor-Criticについて簡単に解説したいと思います。

時刻 $t$ における状態、行動、即時報酬を $s_t$, $a_t$, $r_t$ と書くとき、これらが $s_t, a_t, r_{t+1}, s_{t+1}, a_{t+1}, r_{t+2}, ...$ という順番で決定されるとします。このときQ学習は、行動価値関数 $Q(s, a)$ という状態と行動のペアに対して報酬の期待値の見積もりを返す関数を、状態 $s_{t+1}$ が判明する度に以下の更新式を用いることで求める手法でした:

[[ Q(s_t, a_t)\leftarrow Q(s_t, a_t) + \alpha(r_{t+1} + \gamma\max_a Q(s_{t+1}, a) - Q(s_t, a_t)). ]]

$Q(s_t, a_t)$ は更新を繰り返すと初期値に依らず「最適な行動を取り続けたとき」の報酬 $G_t := r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots$ の期待値（価値とも言います）を見積もった値になります。

Q学習からActor-Criticの方へ一歩進んだ手法にSARSAがあります。SARSAとQ学習は行動価値関数の更新式のみが異なり、SARSAでは行動 $a_{t+1}$ を決定する度に以下の更新式を用います:

[[ Q(s_t, a_t)\leftarrow Q(s_t, a_t) + \alpha(r_{t+1} + \gamma Q(s_{t+1}, a_{t+1}) - Q(s_t, a_t)). ]]

Q学習の更新式とよく似ていますが、$\max_a Q(s_{t+1}, a)$ が $Q(s_{t+1}, a_{t+1})$ に置き換わっている点が異なります。$\max_a Q(s_{t+1}, a)$ も $Q(s_{t+1}, a_{t+1})$ も状態 $s_{t+1}$ の価値を見積もった式ではありますが、状態 $s_{t+1}$ でどのような行動を取るかの想定が異なります。Q学習では実際に取った行動 $a_{t+1}$ とは関係なく、仮に $Q(s_{t+1}, a)$ を最大化する行動を取ったとして $s_{t+1}$ の価値を見積もるのに対して、SARSAでは実際に取った行動 $a_{t+1}$ をもとに $s_{t+1}$ の価値を見積もります。この違いを反映して、SARSAでは $Q(s_t, a_t)$ は更新を繰り返すと初期値に依らず「方策にしたがって行動を取り続けたとき」の報酬 $G_t$ の期待値を見積もった値になります。

実は、前節でみた獲得される方策の違いは、この差を反映したものです。SARSAのように実際の方策に基づいて状態や行動の価値関数を更新する手法を方策オン手法（On-policy）と言い、Q学習のようにそうでない手法を方策オフ手法（Off-policy）と言います。次に紹介するActor-Criticも方策オン手法です。方策オン手法では、$\varepsilon$-greedy法やソフトマックス法による行動のバラつきを考慮して状態や行動の価値を見積もるため、崖に隣接するマスの価値およびそのようなマスに移動しようとする行動の価値を低く見積もります。その結果、崖から少し距離を置いてゴールまで進む行動を獲得するようになるというわけです。

それではActor-Criticを紹介します。Actor-Criticは方策を定めるアクターと、方策評価を行うクリティックという2つのモジュールから構成されます[1]。アクターは内部に効用関数 $q(s, a)$ を持ち[2]、これとソフトマックス法にもとづいて行動を確率的に決定します。具体的には温度パラメータを $T$、指数関数 $e^x$ を $\exp(x)$ と書くとき、ソフトマックス法では状態 $s$ において行動 $a$ を取る確率 $\pi(a | s)$ を以下で定めます:

[[ \pi(a | s) = \frac{\exp(q(s, a)/T)}{\sum_b \exp(q(s, b)/T)}. ]]

この関数は $q(s, a)$ が最大となる $a$ に最も高い確率を割り当てる一方で、その他の $a$ にも一定の確率を割り当てるような式になっています（$\sum_a \pi(a | s) = 1$ なので確率になっています）。温度 $T$ は両者でどれくらい差をつけるかを定めるパラメータです。$T$ が $0$ のとき $q(s, a)$ が最大となる $a$ に確率 1 を割り当てるようになり、逆に $T$ が $\infty$ に近づくと一様分布に近づきます。

一方でクリティックは内部に状態価値関数 $V(s)$ を持ち、アクターの方策にしたがったときの状態の価値を評価します。状態 $s_{t+1}$ が判明する度に、$q(s, a)$ と $V(s)$ を以下のように更新します:

[[ \delta\leftarrow r_{t+1} + \gamma V(s_{t+1}) - V(s_t), ]] [[ V(s_t)\leftarrow V(s_t) + \alpha^{(\rm critic)}\delta, ]] [[ q(s_t, a_t)\leftarrow q(s_t, a_t) + \alpha^{(\rm actor)}\delta. ]]

SARSAとの違いは、状態 $s_{t+1}$ の価値を $Q(s_{t+1}, a_{t+1})$ により評価していたところをそれ専用の関数による値 $V(s_{t+1})$ に置き換えて、$V(s)$ と $q(s, a)$ をそれぞれ別に学習しているところです。そのため学習率のパラメータは $\alpha^{(\rm critic)}$ と $\alpha^{(\rm actor)}$ の2つに増えています。$V(s_t)$ は更新を繰り返すと初期値に依らず「方策にしたがって行動を取り続けたとき」の報酬 $G_t$ の期待値を見積もった値になります。

Actor-Criticの長所として、アクターとクリティックが分かれているために方策を自由に設計できるという点が挙げられます。Q学習やSARSAは行動価値関数 $Q(s, a)$ を使うことが前提とされており、$\varepsilon$-greedy法やソフトマックス法などと組み合わせることを考えると、特に行動は離散変数でないと上手く実装できません。一方Actor-Criticでは、例えば行動確率を直接出力するパラメトリックな関数 $\pi(a | s; {\bm \theta})$ を使うことで、行動が連続変数の場合にも方策を適切にモデル化することが可能です[3]。状態も行動も離散的な崖歩き問題にはあまり関係のない発展的な話題ですが、ついでに知っておくと良いでしょう。

• Actor-Criticは方法の総称で実装方法はさまざまにあり、ここではその一例を紹介しているという点にご注意ください。また前節でトレースの $\lambda$ というパラメータを設定しましたが、ここでは初めから $\lambda = 0$ のケースを解説しているため、そのようなパラメータは登場していません。
• Actor-Criticで得られる $q(s, a)$ は行動価値関数 $Q(s, a)$ とは全く別物です。S⁴ ではPreferenceと呼んでいます。
• この場合、パラメータ $\bm\theta$ を更新することで方策を最適化します。そのような手法を方策勾配法と言います。

終わりに

今回まででエージェントシミュレーションで強化学習を使う例について一通り解説しました。 次回から担当者が変わり、強化学習に関する新しい話題をお届けする予定です。ご期待ください！