S4 で始める強化学習（第5回）エージェントシミュレーションで作ってみる（1/2）

HOME
S4 で始める強化学習（第5回）エージェントシミュレーションで作ってみる（1/2）

2023年4月24日 10:22

本記事は当社が発行しているシミュレーションメールマガジンVol. 10の記事です。シミュレーションメールマガジンの詳細・購読申込はこちらのサポートページから

はじめに

S⁴ で強化学習を使ったシミュレーションモデルを作成してみようという講座の5回目の記事になります。

前回、エージェントシミュレーションで強化学習を使う例として崖歩き問題を紹介し、S⁴ で実行する様子をお見せしました。今回は、モデルの実装方法について詳しく解説します。

実装の方針

エージェントシミュレーションでは、離散イベントシミュレーションに比べてより多くのコードを書く必要があります。そのため、最短手順でモデルを完成させようとすると、途中で躓く可能性が高くなります。このようなときは、まず動くものを作り、それを徐々に拡張するような形でモデルを作成するのがお勧めです。

崖歩き問題について、私は次の3ステップに分けてモデルの作成を行いました。

ステップ1：エージェントが格子グラフ上でランダムウォークするシミュレーションモデルの作成
ステップ2：強化学習モデルの追加
ステップ3：格子グラフのサイズのパラメータ化など細かい機能の追加

ステップ1で、ひとまず動くシミュレーションモデルを作成してしまうことがポイントです。そうすることでステップ2以降で、意図しないコードを書いたときにすぐに気付けるようになります。またこれらのステップの中で躓きやすいのは、ステップ2の強化学習モデルを追加するところだと思います。そのため試行錯誤しやすいように、ステップ2までは必要最小限の機能のみ実装するようにします。強化学習モデルを組み込んだモデルが動くようになれば、ステップ3で安心してモデルを拡張していくことができます。

分量が多いため、今回の記事ではステップ1までを解説します。ステップ1の完成形のプロジェクトは、こちらからダウンロードいただけます。 S⁴ をお持ちの方は、プロジェクトをインポートして適宜参照してください。

※ S⁴ のversion 6.3をご利用の方は修正パッチが出ていますので、こちらから修正パッチをダウンロードして実行した後、プロジェクトを動かしてください。

ステップ1：ランダムウォークモデルの作成

S⁴ で新規プロジェクトを作成したら、左のブラウザから「エージェント / 同期エージェント」と「環境 / 格子グラフ」、「グラフ / グラフ（Graph）」部品を右のエディタへドラッグ&ドロップします。グラフについては名前を「エピソードあたり報酬」に変更しておきます。

環境の設定

まずは格子グラフの設定から行います。「格子グラフ」をダブルクリックして開き、属性設定タブの「格子グラフの幅」と「格子グラフの高さ」をそれぞれ6、3と設定し、「格子グラフの接続方式」を4方格子とします。

次に「環境のカスタムコード」を開き、あとで利用するメソッド（クラスの持つ関数のこと）を定義していきます。実際にモデルを作成するときには、はじめからメソッドを揃えておくのではなく必要に応じて適宜追加していくのが普通ですが、説明の便宜上はじめにまとめて紹介します。次のような編集画面でコードを書いていきます。

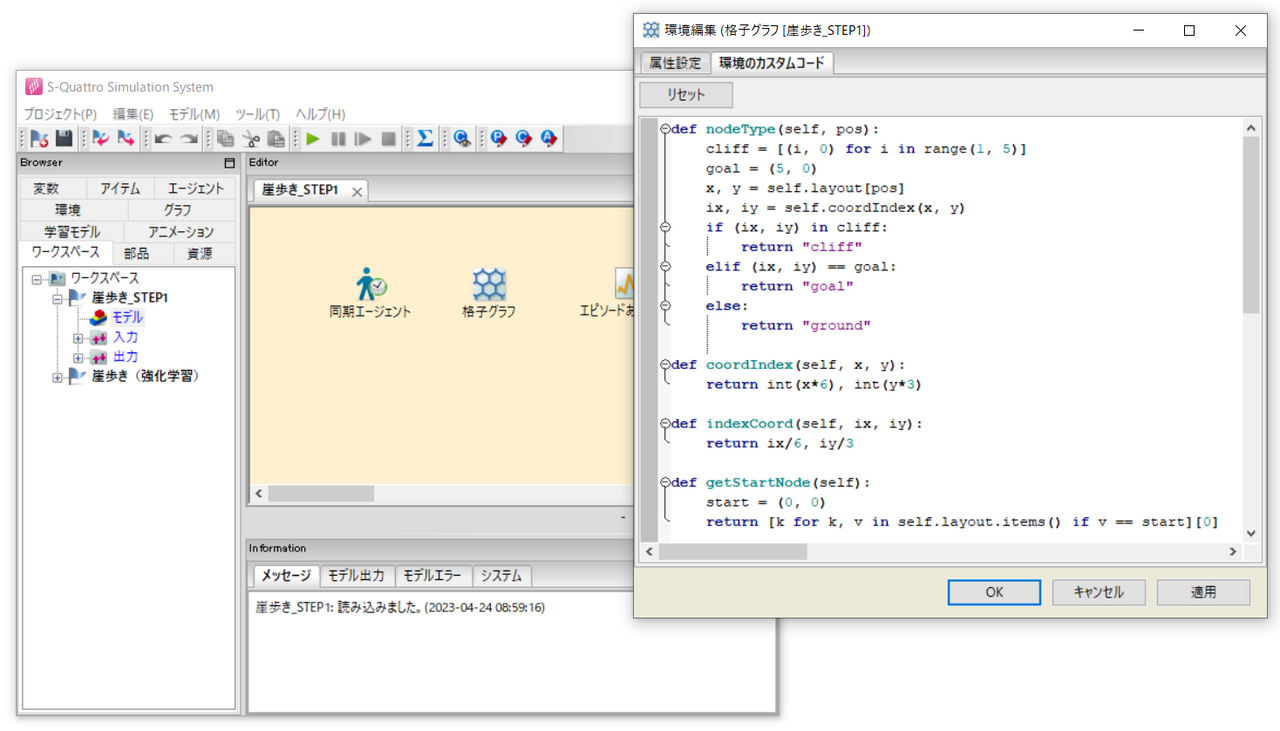
コード編集

メソッドを定義するにあたって、格子グラフの持つlayout変数が何度も登場します。 layout変数は、格子グラフのノード番号をキー、ノード座標 $(x, y)$ を値とする辞書型のデータです。 S⁴ では、エージェントの位置を基本的にノード番号で管理しているので、それをノード座標に置き換える処理を書くことが多々あります。そのような時にlayout変数が参照されます。

それでは、定義したメソッドの概要を紹介します。コードの詳細はサンプルプロジェクトを参照ください。

nodeType(self, pos)
ノード番号を引数として受け取り、ノードの種類を返します。判定するノードの種類は、"cliff"（崖）、"goal"（ゴール地点）、"ground"（平地）の3種類です（スタート地点の場合も"ground"と返します）。この処理を実現するために、layout変数を用いてノード番号をノード座標に変換しています。さらにノード座標は $0$ 以上 $1$ 以下の実数値なので、これを整数インデックスに変換しています。格子グラフの座標系は左下を原点 $(0, 0)$ とし、$x$ 軸は右方向に、$y$ 軸は上方向に伸びています。したがって、前回の記事の図と位置関係が合うように、インデックスが $(1, 0)$、$(2, 0)$、$(3, 0)$、$(4, 0)$ のとき崖、$(5, 0)$ のときゴール地点、それ以外のとき平地と判定しています。

coordIndex(self, x, y)
座標を引数として受け取り、インデックスを返します。

indexCoord(self, ix, iy)
インデックスを引数として受け取り、座標を返します。

getStartNode(self)
スタート地点のノード番号を返します。 layout変数の中身を一通り調べ、値がスタート地点の座標である $(0, 0)$ に一致するキーを返しています。リスト内法表記により簡潔なコードになっています。

getNextNode(self, node, dir)
ノード番号と方向を表す整数（0~3）を引数として受け取り、指定したノードから指定した方向へ移動した先のノード番号を返します。移動先のノードが存在しない場合（例えばスタート地点から左に行こうとしたときなど）、Noneを返します。

getValidDs(self, node)
ノード番号を引数として受け取り、指定したノードから移動可能な方向をリストで返します。

格子グラフの設定は以上です。

エージェントの設定

次に同期エージェントを設定します。「同期エージェント」をダブルクリックして開き、属性設定タブの「環境オブジェクト」としてeLatticeGraph(格子グラフ)を選びます。

属性設定タブの「エージェントの初期化処理」「エージェントのステップ処理」「エージェント集合の初期化処理」を設定していきます。エージェントシミュレーションでは、大体これらの項目を編集することが多いです。場合によっては「エージェント集合のステップ処理」を編集することもあります。

以降の内容を理解する上で、エージェント、エージェント集合、環境（格子グラフ）の関係を抑えておくことが重要です。S⁴ では、これら3つのオブジェクトを組み合わせることでエージェントシミュレーションを実現しますが、エージェントはエージェント集合に属し、エージェント集合は環境に属します。

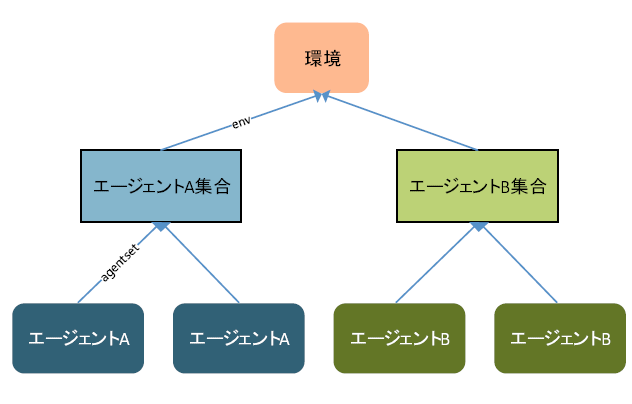
クラスの階層関係

したがって、例えばエージェントから先ほど定義したnodeTypeメソッドにアクセスするには、「エージェント.agentset.env.nodeType」などと記述します。またこれらの他にシミュレーターというオブジェクトが存在し、シミュレーターには例えば「エージェント.simulator」などと、どのオブジェクトからも直接アクセスできます。なお今回の実装では、エージェント集合は1つのみですが、例えば人の他に車が登場するなど、行動ルールの異なる複数のエージェントを扱う場合には、エージェント集合を複数用意します。

それでは、「エージェントの初期化処理」から設定していきます。ここにはエージェントが作成されるタイミングで行う処理を記述します。属性設定タブから編集画面を開き、以下のコードを入力します。

self.setPosition(self.agentset.env.getStartNode())
self.screenSize = 40
self.rewardSum = 0

上2行は S⁴ 独自の書き方で、1行目で初期化の際にエージェントをスタート地点に出現させること、2行目で描画の際のエージェントのサイズを40ピクセルとすることを指定しています。 3行目でゴール地点に到達するまでの報酬の総和を記録しておくための変数を準備しています。

次に「エージェント集合の初期化処理」を設定します。ここにはエージェント集合が作成されるタイミングで行う処理を記述します。属性設定タブから編集画面を開き、以下のコードを入力します。

self.agentFreezeVars = [""] # エージェントの凍結する変数リスト

self.monitor = TimeMonitor(["エピソード番号", "報酬"], ["i", "f"], name="報酬の記録")
self.simulator.addMonitor(self.monitor)

# エージェントの生成
n = 1 # エージェントの生成数
self.keys = keys
self.episode = 0
self.generateAgents(n, **keys)

1行目はデフォルトで記述されているコードで、今回は気にしなくて良いです。 3行目、4行目でTimeMonitorというエピソードごとの報酬を記録するための部品を定義しています。これの使い方は後ほど説明します。 10行目でエージェントを1人生成しています。その引数であるkeysを8行目でkeys変数に記録し、9行目でエピソード数を記録するための変数を準備しています。

最後に「エージェントのステップ処理」を設定します。ここには毎時刻にエージェントが行う処理を記述します。属性設定タブから編集画面を開き、以下のコードを入力します。

v = self.getPosition()
env = self.agentset.env
if env.nodeType(v) == "goal": # ゴールした場合はエピソードの終了処理を行う
    self.rewardSum += 10
    self.agentset.episode += 1
    self.agentset.monitor.observe(now(), self.agentset.episode, self.rewardSum)
    self.agentset.remove(self)
    # 次のエージェント（=エピソード）作成
    self.agentset.generateAgents(1, **self.agentset.keys)
elif env.nodeType(v) == "cliff": # 崖に落ちた場合はスタート地点に戻る
    self.rewardSum -= 100
    self.setPosition(env.getStartNode())
else:
    self.rewardSum -= 1
    ds = env.getValidDs(v)
    d = next(sample(ds))
    v_next = env.getNextNode(v, d)
    self.setPosition(v_next)

1行目でgetPositionメソッドにより、現在位置のノード番号を取得します。そしてnodeTypeメソッドにより、ノードの種類を判定し、それに基づいて処理内容を切り替えます。

ゴール地点の場合は次の処理を行います。報酬の10をrewardSumに追加します。 episode変数の値を1増やし、現在時刻now()、報酬の総和rewardSumとともにTimeMonitorのobserveメソッドに渡します。 observeメソッドがこれらの値を記録することで、これらの値をシミュレーション後に参照できるようになります。そしてremoveメソッドによりエージェント集合からエージェントを削除し、generateAgentsメソッドにより次のエージェントを生成します。同じエージェントを使い回さずに、新しくエージェントを生成するのは、後で導入する強化学習モデルが１エージェントを１エピソードと捉えて学習を行うためです。

崖の場合は次の処理を行います。まず報酬の-100をrewardSumに追加します。次にsetPositionメソッドによりスタート地点にエージェントを移動させます。

平地の場合は通常の移動処理を行います。まず報酬の-1をrewardSumに追加します。次に先ほど定義したgetValidDsメソッドにより、移動先の候補をリストで取得し、next(sample(ds))によりランダムに1つ選択します（これもS⁴ 独自の書き方です）。そして、setPositionメソッドにより選択したノードにエージェントを移動させます。

同期エージェントの設定は以上です。ここまででモデルは動かせるようになります。

グラフの設定

最後に、TimeMonitorで記録したエピソードあたり報酬をグラフで可視化してみましょう。これについては必要最小限の機能なのか疑問に思われる方もいらっしゃるかもしれません。しかし、エピソードあたり報酬の可視化は、強化学習モデルを導入する前に是非とも実装しておきたい機能です。なぜなら、獲得報酬の移り変わりを見ることで、エージェントの学習が順調かを簡単に判断することができ、コードの不備などにより学習が上手くいかなかったときにすぐに気付けるようになるからです。そういう意味で、動くシミュレーションモデルを手に入れるのと同じくらい、エピソードあたり報酬の可視化の実装には価値があります。

グラフを作成するにあたって、一度シミュレーションを実行しておきましょう。メニューバーから「パラメータを編集する」をクリックし、シミュレーション終了時間を10000秒にしておきます。その後、シミュレーションを実行します。アニメーションを閉じると、すぐに最後まで実行されるかと思います。

シミュレーション実行後、「エピソードあたり報酬」をダブルクリックして開き、折れ線グラフを追加します。その際、グラフデータという欄の1行目に、xとして「default/報酬の記録(出力)/エピソード番号(整数)」を選択し、yとして「default/報酬の記録(出力)/報酬(実数)」を選択します。すると横軸をエピソード番号、縦軸を報酬とする折れ線グラフが表示されるはずです。今の段階では、エージェントはランダムに動くだけなので、基本的に負の方向に大きい値を取っていることが確認できるかと思います。

今回は、崖歩き問題の実装について、3ステップに分けたうちのステップ1までを丁寧に解説しました。次回、残りの実装について解説する予定です。