ここでは、社会システムシミュレーションの理解を深めて頂く上で、よく使われる例題の紹介と、各例題のモデルプログラム(S4 Simulation System Ver4.2以降で動作します)を公開しています。 社会システムシミュレーションの理解や業務への応用にもご活用ください。 こちら からも一括でダウンロード頂けます。
S4 Simulation System のテスト利用のお申し込みはこちら よりお問い合わせください。
例題のラインナップやモデル設計は、高橋 真吾 先生(早稲田大学 創造理工学部 教授/社会シミュレーション研究所 所長)に監修頂いております。
目次
シェリングの分居モデル
シェリングの分居モデルは、社会科学におけるエージェントベースモデリングの先駆けとも言われているモデルで、1971年にアメリカの経済学者であるトーマス・シェリングによって発表されました。
周囲の 2/3 (=類似度) 近くが異人種でも満足する「寛容な」人を想定してみると、直観的には棲み分けは生じにくいと思われますが、実はそうではありません。 個々の人間は寛容でも、社会全体を眺めると分居が進むとされています。また、類似度の閾値は高すぎても低すぎても棲み分けが進まないとされていますが、シミュレーションでもこれを確認する事が出来ます。
モデル概要
セル空間上にランダムに配置された2種類のエージェントを考える
以下の処理を繰り返し行う
セル空間上の全てのエージェントに対し、類似度を計算する
a: 近傍にいる同類 (自分自身を含めない) エージェントの数
エージェントは、類似度が閾値以下の時、移動可能なセルにランダムに移動する
幸福度を計算する
幸福度 = (類似度の閾値を超えているエージェント数 / エージェントの総数) × 100
全てのエージェントが移動しなくなると (幸福なとき) 終了
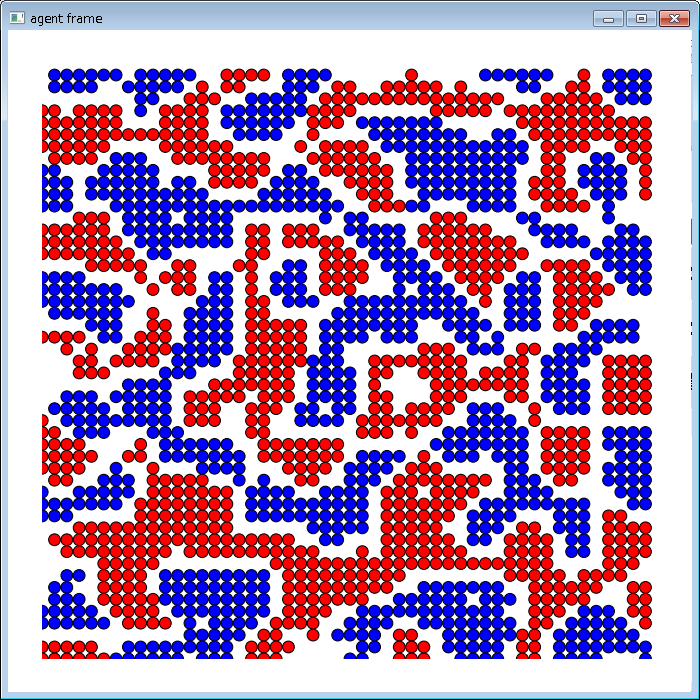
棲み分けの様子
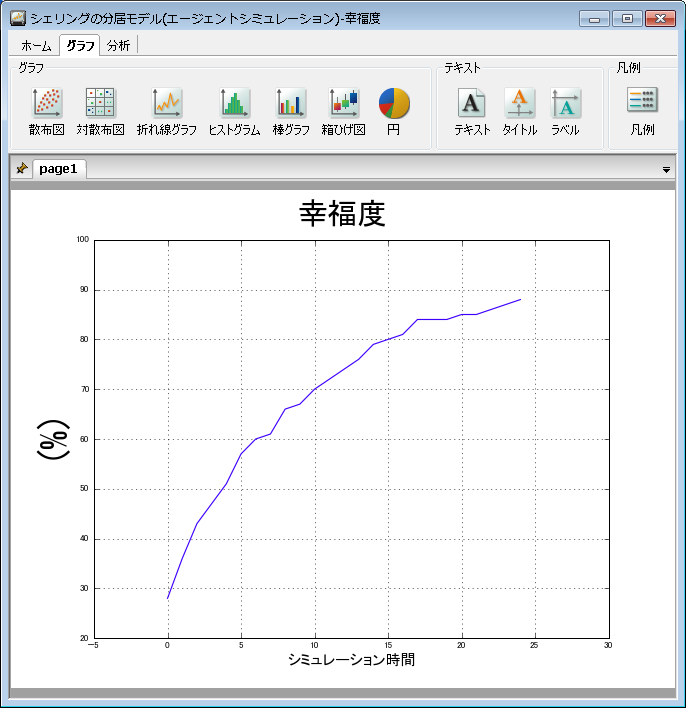
エージェントの幸福度
モデルのダウンロード S4 Simulation System Ver4以前をご利用の方 ( Segregation.sss ) S4 Simulation System Ver5以降をご利用の方 ( Segregation.s4 )
ライフゲーム
ライフゲームは、生命の誕生、進化、淘汰などのプロセスをモデル化したものです。1970年にイギリスの数学者ジョン・ホートン・コンウェイによって作られました。
このモデルは、生物集団においては、過疎でも過密でも個体の生存に適さないとしたモデルです。
ライフゲームではシミュレーションを進めると、生き延びる場合の変化は 4 パターンに分類されます。
・固定物体 例. 振動子の様子
モデル概要
セル空間上に「生」の状態と「死」の状態のエージェントを設定する
「生」の状態のエージェントは、周囲 ( 1 近傍) のエージェントの状態によって、下記のどれかの状態に変化する
セル空間上の全てのエージェントに対し、類似度を計算する
死の状態のエージェントは、周囲 ( 1 近傍) のエージェントの状態によって、下記のどれかの状態に変化する
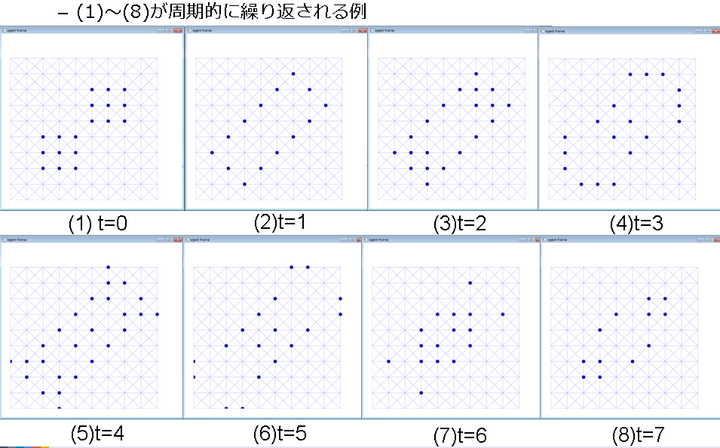
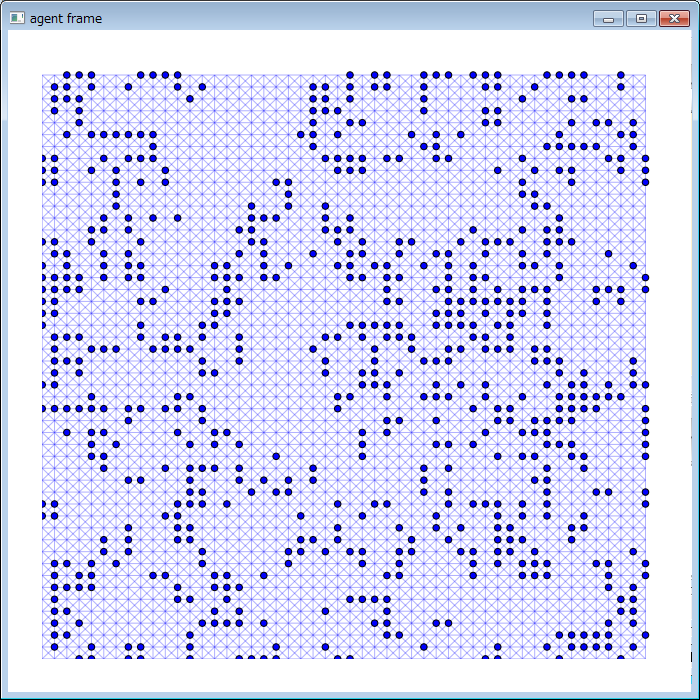
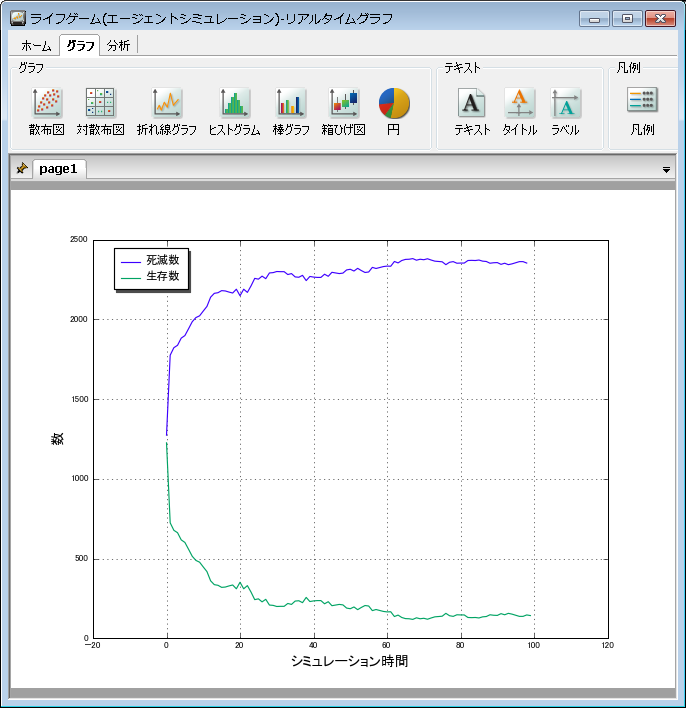
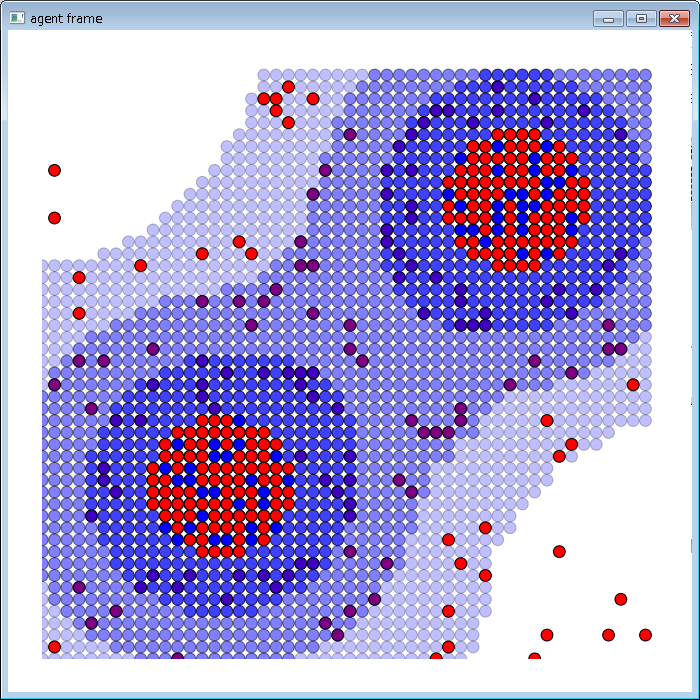
ライフゲームの様子
各細胞数の状態変化
モデルのダウンロード S4 Simulation System Ver4以前をご利用の方 ( LifeGame.sss ) S4 Simulation System Ver5以降をご利用の方 ( LifeGame.s4 )
SugarScape
SugarScape モデルは、Joshua M. Epstein と Robert Axtell によって提唱された社会シミュレーションモデルです。 このモデルは人工社会のモデルとして、広く用いられています。
モデル概要
セル空間上の各セルの最大 Sugar 量と、エージェントを配置する
各エージェントの Sugar 初期量、視野 ( 移動可能なセル数 )、1 ステップ辺りの Sugar 消費量をランダムに設定する
セル空間上のエージェントは順番に以下を繰り返す
a.視野内のセルの内、他のエージェントがいない、Sugar 量最大のセルを選択し、移動する。候補が複数ある場合には、最も近いセルに移動する。
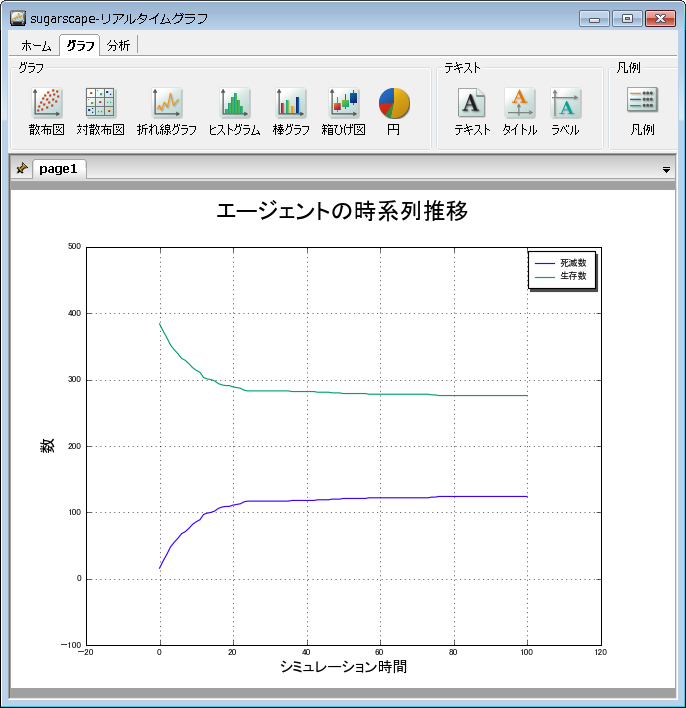
エージェントの様子
エージェントの生存数と死滅数の推移
モデルのダウンロード S4 Simulation System Ver4以前をご利用の方 ( SugarScape.sss ) S4 Simulation System Ver5以降をご利用の方 ( SugarScape.s4 )
このモデルには様々な拡張があります。例えば、エージェントが保持するものが、Sugar だけでなく、Spice という2つ目の量を持たせるとどうでしょうか。 エージェントは Sugar と Spice の両方を考慮した行動をするはずです。また、「Sugar は 0 に近いが、Spice を十分に持っているエージェント」と、「Spice は 0 に近いが、Sugar は十分に持っているエージェント」が出会ったら、どうなるでしょうか。
このモデルには様々な拡張があります。例えば、エージェントが保持するものが、Sugar だけでなく、Spice という2つ目の量を持たせるとどうでしょうか。 エージェントは Sugar と Spice の両方を考慮した行動をするはずです。また、「Sugar は 0 に近いが、Spice を十分に持っているエージェント」と、 「Spice は 0 に近いが、Sugar は十分に持っているエージェント」が出会ったら、どうなるでしょうか。
モデルのダウンロード S4 Simulation System Ver4以前をご利用の方 ( SugarScape_spice.sss ) S4 Simulation System Ver5以降をご利用の方 ( SugarScape_spice.s4 )
ゴミ箱モデル
組織における意思決定のメカニズムを記述した代表例として、ゴミ箱モデル ( March and Olsen (1976)) があります。
実際にゴミ箱モデルでは、組織における意思決定は合理的には行われておらず、むしろ合理性を欠く形で行われているとしてモデル化されています。 この場合の合理性とは秩序のない意思決定 (一貫性のない問題選択、不明確な技術、流動的な参加) です。
モデル概要
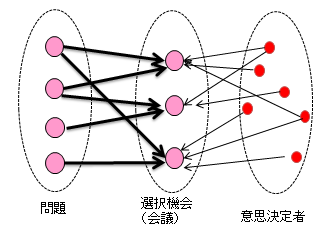
問題、選択機会、意思決定者からなる集合を組織とし、意思決定はこれらの相互作用でなされるものと考える
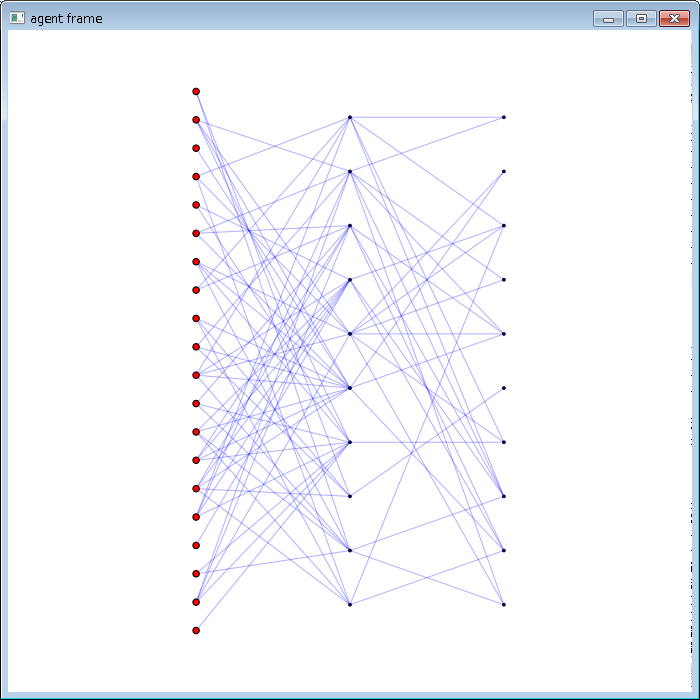
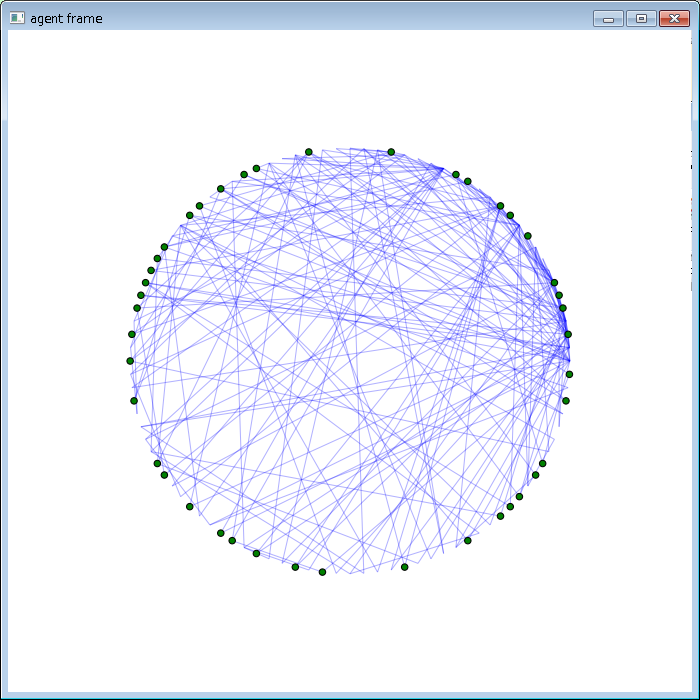
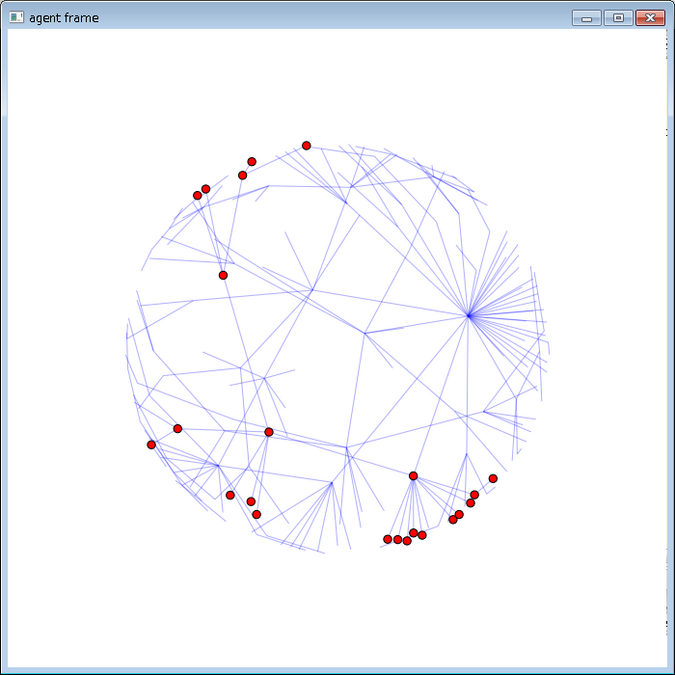
問題、選択機会、意思決定者の構造をグラフ構造に表現する
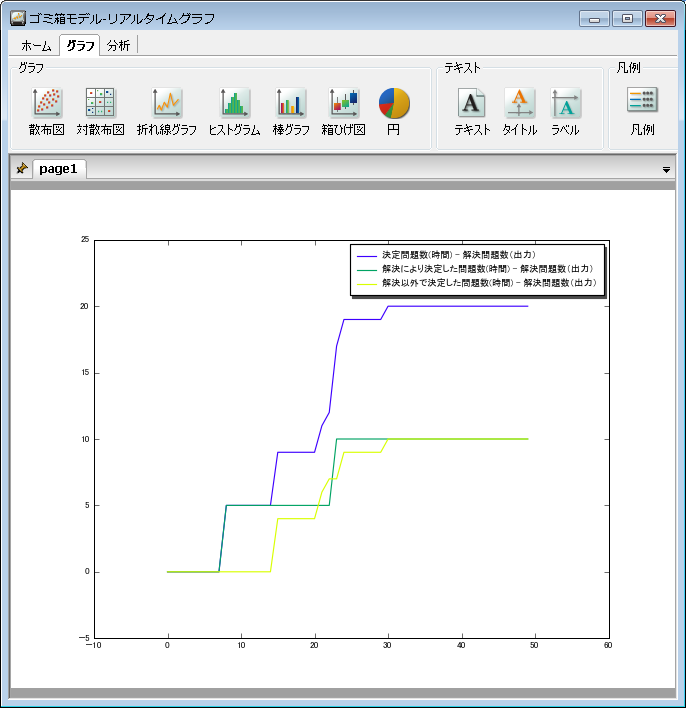
未解決の問題は、選択機会で取り上げられ、意思決定者は選択機会へエネルギーを注入する。選択機会で得られたエネルギーの累積量によって、問題は解決される
組織 (グラフ構造) ゴミ箱モデルシミュレーション 決定問題数の変化
モデルのダウンロード S4 Simulation System Ver4以前をご利用の方 ( GarbageCan.sss ) S4 Simulation System Ver5以降をご利用の方 ( GarbageCan.s4 )
繰り返し囚人のジレンマ
「繰り返し囚人のジレンマ」を紹介する前に、まずは、「囚人のジレンマ」がどのような問題かをご紹介します。
囚人のジレンマ問題
共同で犯罪を行ったと思われる囚人 A、B が取り調べを受けています。取調官は、自白させるため以下を持ちかけました。
2 人とも黙秘したら、2 人とも懲役 2 年だ
1 人だけが自白したら自白した者は釈放 (懲役 0 年) してやる。自白しなかった方は懲役 10 年だ
2 人とも自白したら、2 人とも懲役 5 年だ
さて、2 人の囚人は共犯者と協調して黙秘すべきか、それとも共犯者を裏切って自白すべきでしょうか。 それぞれのケースを表にまとめると次のようになります。
囚人 B
協調
裏切り (自白)
囚人 A
協調
( 2 年、2 年)
( 10 年、0 年)
裏切り (自白)
( 0 年、10 年)
( 5 年、5 年)
利得表
2 人の囚人にとっては、互いに裏切り合って 5 年の刑を受けるよりは、互いに協調し合って 2 年の刑を受ける方が得です。 しかし、囚人達が自分の利益のみを追求している限りにおいては、互いに裏切り合うという結末を迎えてしまう、という問題が囚人のジレンマ問題です。
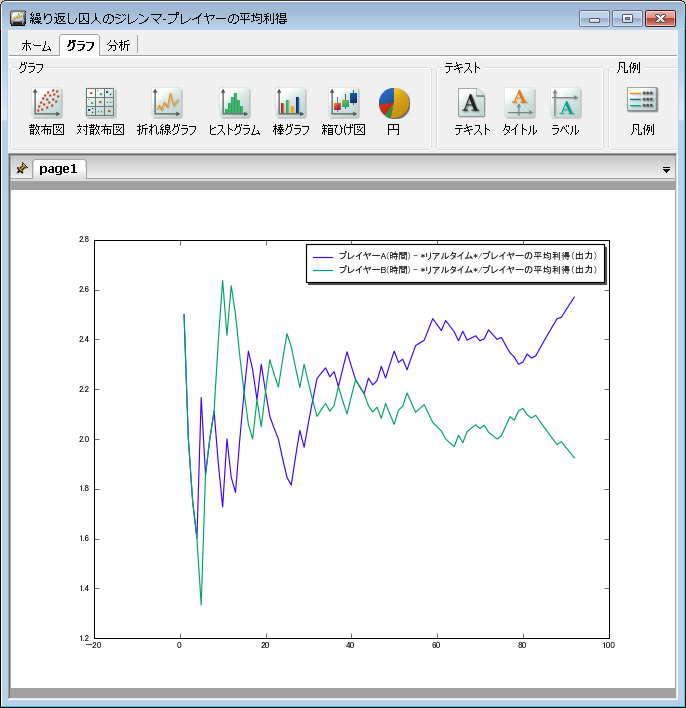
繰り返し囚人のジレンマは、このような囚人のジレンマ問題を 2 人で繰り返し行うゲームです。1 回の囚人のジレンマでは戦略的には裏切るべきです。 ただし、これを繰り返すと、必ずしも裏切るという戦略が有利になるとは限りません。
random:
各プレイヤーの利得の推移
モデルのダウンロード S4 Simulation System Ver4以前をご利用の方 ( PrisonerIterated.sss ) S4 Simulation System Ver5以降をご利用の方 ( PrisonerIterated.s4 )
繰り返し N 人の囚人のジレンマ
繰り返し囚人のジレンマではプレイヤーは 2 人でした。これをさらに N 人で繰り返し行うのが、繰り返し N 人の囚人のジレンマです。
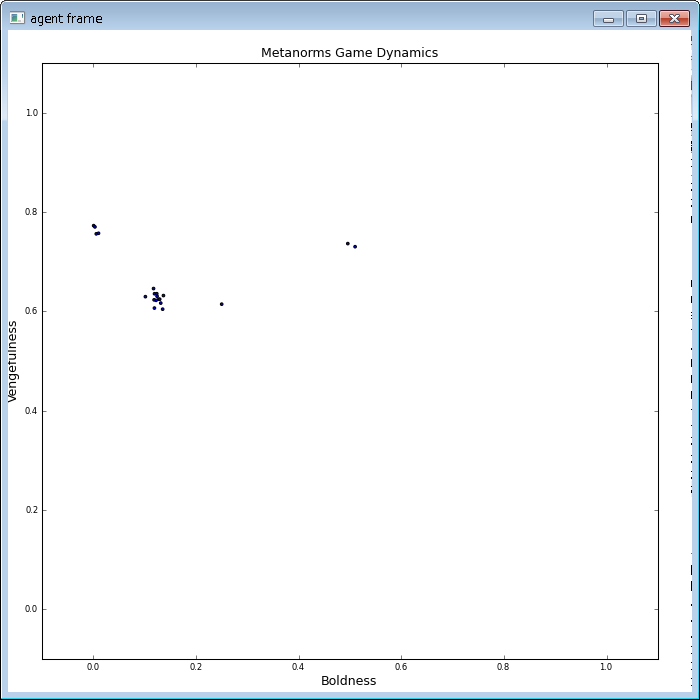
メタ規範ゲームは Axelrod (アクセルロッド) が集団における秩序 (協調的な社会) をモデル化したものです。モデルは N 人の囚人のジレンマを拡張したものであり、 非協調者 (裏切者) を罰するという行動原理 (規範) をモデルに導入しています。ただし、シミュレーションしてみると、規範だけでは秩序は達成されず、非協調者が支配的な社会となってしまいます。
学級問題
あるクラスではいじめ(裏切り)が問題になっています。ある日、ある生徒がいじめをしているところを別の生徒に発見されました。発見された生徒は、もちろん注意を受けます
(規範)。 ただし、これだけではクラスからいじめはなくなりませんでした。陰でいじめを見ているだけの生徒が数多くいた為です。
路上喫煙問題
ある行政区では、路上喫煙が条例で禁止されています。条例では、路上喫煙者を発見した者は、それを監視員に通報すると、違反者は罰金が科せられるように決められています (規範)。違反者を減らすさらなる対策を考えた場合、メタ規範ゲームに従うと、違反者を発見した者が、通報しなかった事が判明した場合、その者も罰金を払うようにするとさらに効果が得られそうです。
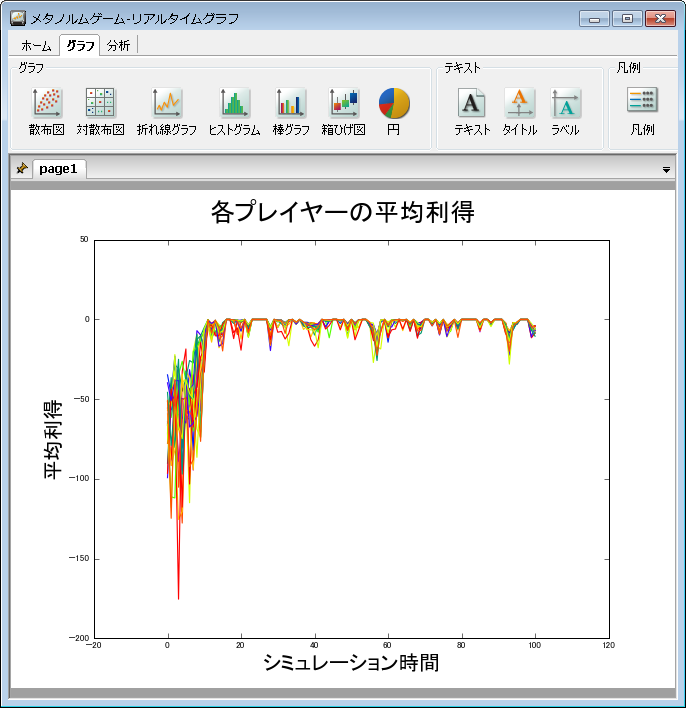
メタ規範ゲームによる各プレイヤーの推移
各プレイヤーの平均利得の推移
モデルのダウンロード S4 Simulation System Ver4以前をご利用の方 ( MetaNormGame.sss ) S4 Simulation System Ver5以降をご利用の方 ( MetaNormGame.s4 )
オークション
オークション理論とは Vickrey (1961) の分析が契機となって発展したミクロ経済学の一部で、売り手と買い手が公平になる為に考えられた市場のメカニズムを設計する為の理論となります。
種類
特徴
例
備考
公開オークション
英国式オークション (競り上げ式オークション)
開始時に売り手が最低金額を提示し、買い手が徐々に値段を釣り上げていく方式。最高額を提示した買い手が購入。
絵画の競り
売り手が不利。
公開オークション
オランダ式オークション (競り下げ式オークション)
開始時に売り手が最高金額を提示し、売り手が徐々に値段を下げていく方式。買い手の一人が買う意思を示すと、その買い手に販売される。
バーゲンセール
最適な戦略は存在しない。
封印オークション
第 1 価格オークション
他者に価格が分からないようにして行う方式。希望額を紙に書いて売り手に渡す (入札)。最高額を入札した者が自分の入札額で購入。
公共事業の入札。
購入できた際にもっと低い金額で購入できたかもしれない。最適な戦略は存在しない。
封印オークション
第 2 価格オークション
他者に価格が分からないようにして行う方式。希望額を紙に書いて売り手に渡す (入札)。最高額を入札した者が 2 番目に高い額で購入。
(RTB) Real-Time Bidding
自分の入札額を下げても、2 番目の価格で購入するので購入価格は変わらない。誰にとっても、他人を気にすることなく自分の買いたい価格を入札することが最適な戦略となる。
ネットオークション
自動入札方式
イングリッシュオークションとセカンドプライスオークションの中間。
yahooオークション等
その他にも以下のオークションがあります。
フラワーオークション
オランダ式オークションで、花 1 本 (単位) の価格を入札し、落札者が購入数量を決める方式です。余剰の財が発生した場合には、余剰分は再度オークションされます。
一律価格封印オークション
「 p 以下の任意の価格で q の量を購入する」(需要量と受け入れ価格の双方) 注文を入札する方式です。国債等の入札で利用されています。
同時上昇オークション (SAA) 及び時計オークション
オークション対象財の複数に同時に入札を行うことが出来ます。電波帯域の利用免許のオークションで利用されています。
パッケージオークション
入札者が複数の財を組み合わせて、パッケージとする事ができます。パッケージごとに値段が異なる為、財の数が増加すればするほど複雑なメカニズムになります。 近年では、空港の発着枠や発電ポートフォリオの売却で利用される。
ここでは、インターネットオークションのモデル例についてご紹介します。インターネットオークションの形態には低い価格から始まり、その価格から高い金額を提示して競っていく方式があります。 この時入札者の行動は以下に分類することが出来ます※。
EarlyBidder
CheepEarlyBidder
Sniper
SniperByContinuation
行動特性
オークション序盤から入札行動を開始し、各エージェントの上限金額の範囲内で終了時まで入札を行う。
安い価格に反応し、特にオークション序盤の価格が低いときに頻繁に上限金額以内で入札を行う
オークション終了間際にのみ入札行動を行い、上限金額範囲内で 1 回のみ高めの価格を入札する
オークション終了間際にのみ入札行動を開始し、上限金額以内で小刻みに入札を行う。
入札開始
序盤
序盤
終盤
終盤
知覚確率
10~20%
10~30%
70~80%
50~70%
入札確率
10~20%
10~30%
70~80%
30~70%
入札上限金額分布
[1/4p,3/4p]
[1/5p,1/2p]
[1/2p,5/6p]
[1/2p,4/5p]
入札上乗せ金額特性値
25%以下
20%以下
100%以下
50%以下
※[菅原梢, 松田聖] 出品者サイドの落札価格最適化を図るネットオークションモデルの提案・検証 情報処理学会研究報告 2005-03-19 より引用
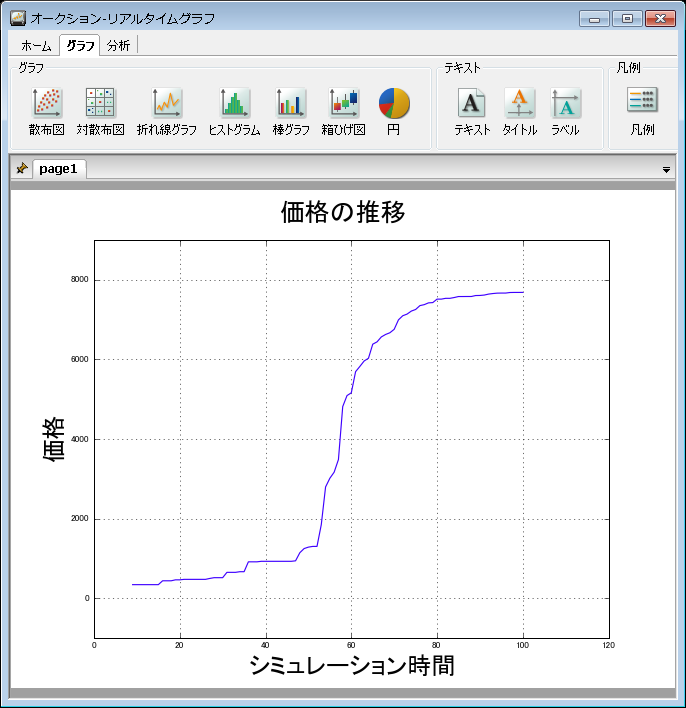
出品される品物は 1 つであり、参加者は品物の出品情報を知ります。出品情報を知ったエージェントは入札可能な金額であれば、入札し現在価格が更新されます。 これを繰り返して、品物が落札されます。シミュレーションモデルでは、価格の更新や落札価格をシミュレーションによって算出します。
価格の推移
モデルのダウンロード S4 Simulation System Ver4以前をご利用の方 ( Auction.sss ) S4 Simulation System Ver5以降をご利用の方 ( Auction.s4 )
商品の普及モデル
新商品は情報発信や、商品を実際に購入したお客の口コミ等によって普及していきます。新商品を全ての顧客層に購入されるようなヒット商品とする為には、商品普及のキーとなるような顧客層に受け入れられるような効果的なマーケティング戦略を立てる必要があります。ここでいう顧客層とは、イノベーター理論 ( 1962年エベレット・M・ロジャース教授) に基づいた、商品の採用者を新商品購入の早い順に以下の五つに分類したものを指します。
Innovators
EarlyAdopters
Early Majority
Late Majority
Laggards
行動特性
冒険心にあふれ、新しいものを進んで採用する人
流行に敏感で、情報収集を自ら行い、判断する人。
較的慎重派な人。平均より早くに新しいものを取り入れる。
比較的懐疑的な人。周囲の大多数が試している場面を見てから同じ選択をする。
最も保守的な人。流行や世の中の動きに関心が薄い。イノベーションが伝統になるまで採用しない。
市場割合
2.50%
13.50%
34.00%
34.00%
16.00%
新商品が発売されるとまずイノベーターによって購入されます。次に広告のような情報発信が行われるとその情報を収集したアーリーアダプターによって購入されます。 その後、アーリーアダプターの口コミによって新商品はアーリーマジョリティにまで伝搬され、周囲の大部分によって購入された時にレイトマジョリティによって購入されはじめます。
もしも効果的な情報発信が行われ、その効果が大きい場合には、一定期間後に全ての顧客層にまで商品が普及します。
モデル概要
消費者同士のつながりをネットワーク構造 ( BarabasiAlbert グラフ) として考える
行動特性別市場割合に基づいて、消費者をネットワーク上の各ノードに配置する
シミュレーションが開始されてからある時刻までは、Innovators によって購入される
その後、ある一定期間は、EarlyAdopters が購入する
EaryAdopters と接触した (ノードが隣り合っている) EarlyMajority が購入する
市場全体の 8 割が購入すると、LateMajority が購入を開始する
商品の普及の様子
モデルのダウンロード S4 Simulation System Ver4以前をご利用の方 ( ProductDiffusion.sss ) S4 Simulation System Ver5以降をご利用の方 ( ProductDiffusion.s4 )
現在多くの企業では消費者とのコミュニケーションを図る為に SNS を積極的に活用し始めています。企業が SNS 上に広告等の情報を発信し、
その情報が伝搬していく様子をシミュレーションする事で、情報が伝わる速さやその広がりの程度が把握できます。
モデル概要
SNS でつながっているユーザの構造はネットワーク構造になっている
情報発信者は、SNS 上に情報を発信し、情報発信者と直接つながっているユーザに情報を拡散する
情報発信者からの情報を見たユーザは、その情報を別のユーザへ情報を拡散する
情報を受け取ったユーザは、つながっている別のユーザへ情報を拡散する (繰り返される)
情報伝播の様子
モデルのダウンロードS4 Simulation System Ver4以前をご利用の方 ( InformationDiffusion.sss ) S4 Simulation System Ver5以降をご利用の方 ( InformationDiffusion.s4 )
SIR モデル
伝染病のモデルとしては、古典的な Kermack-McKendrick (1927) の SIR モデルがよく用いられます。非感染者 ( S ) が感染者に接触すると接触時間に比例した確率で感染 ( I ) します。 また、感染者 ( I ) は、感染後の経過時間に比例した確率で治癒 ( R ) します。また、一度感染すると、抗体ができるため再感染はしません。 このモデルは、システムダイナミクスという方法で以下のようにモデル化出来ます。感染症の伝播を S (非感染)、I (感染)、R (回復) の3つの状態量の変化 ( SIR モデル) でモデル化する方法です。
[[
\beta: 感染率, \gamma: 治癒率 \\
\begin{aligned}
\frac{\mathrm{d}S}{\mathrm{d}t} &= -\beta SI \\
\frac{\mathrm{d}I}{\mathrm{d}t} &= \beta SI - \gamma I \\
\frac{\mathrm{d}R}{\mathrm{d}t} &= \gamma I \\
S + I + R &= \mathrm{Const.}
\end{aligned}
]]
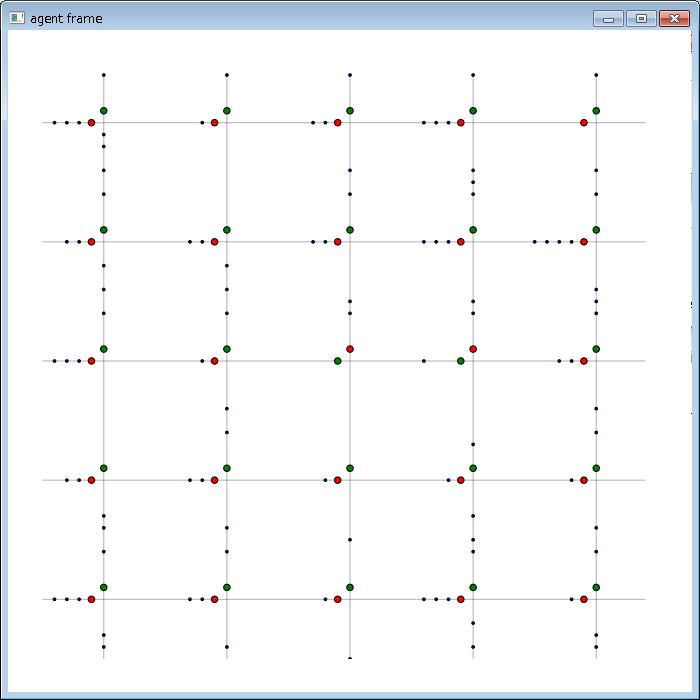
このモデルを使って感染者数、非感染者数の変化をシミュレーションする事もできますが、ここでは、各個人の学校 (職場)、自宅の往復を加味した上で、感染の広がりを考えてみます。
モデル概要
シミュレーションの粒度は、昼、夜の 2 つ
各個人はスケジュールに基づいて、自宅、職場、学校間を移動する
各場所で接触した者同士は、感染率 β で感染する
感染した者は治癒率 γ で治癒する
一度感染した者は再度感染する事はない
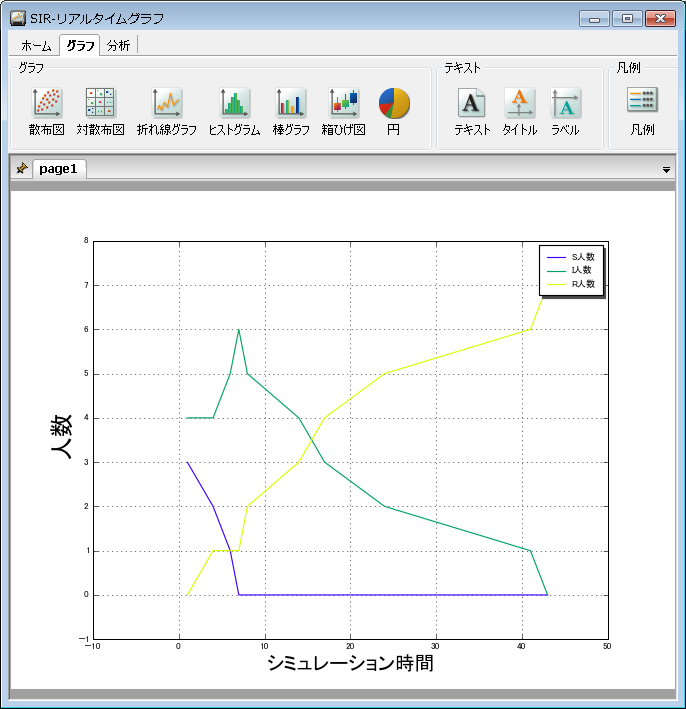
状態別 ( S, I, R ) の人数の推移
モデルのダウンロード S4 Simulation System Ver4以前をご利用の方 ( SIR.sss ) S4 Simulation System Ver5以降をご利用の方 ( SIR.s4 )
渋滞モデル
渋滞をモデル化した数理モデルには、待ち行列理論、流体モデル、追従モデル、セルオートマトンモデルがありますが、ここではセルオートマトンに基づいたシミュレーションモデルをご紹介します。
モデル概要
セル空間上の道路に自動車をランダムに配置
一方通行の道路を自動車が走行する
交差点での右折、左折は考えず、直進のみとする
自動車はシミュレーション 1 ステップあたり、1 セル移動する
交差点が赤になった場合には、車は停止する
前方の車が停止している場合には、車は停止する
交通流シミュレーションの様子
モデルのダウンロード S4 Simulation System Ver4以前をご利用の方 ( Traffic.sss ) S4 Simulation System Ver5以降をご利用の方 ( Traffic.s4 )
おわりに
シミュレーションについて
他にもシミュレーションで解決できる課題の例をシミュレーション適用事例 としてご紹介しています。 1から分かるシミュレーション読本 】を無料公開しています。 よろしければ併せてご覧ください。
S4 Simulation System について
▼複雑なモデルをGUI上で表現し、シミュレーションを行なえる4 Simulation Systemについてはこちらhttps://www.msi.co.jp/solution/s4/top.html
30日間の無償トライアルでシミュレーションモデルをご自身で動かしていただくことも可能です。ご興味をお持ちの方は下記のフォームからお問い合わせください。
お問い合わせはこちら