- HOME
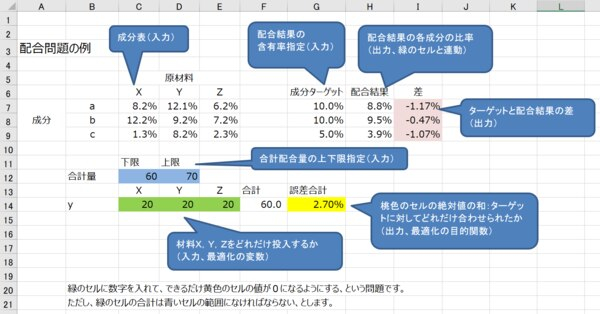
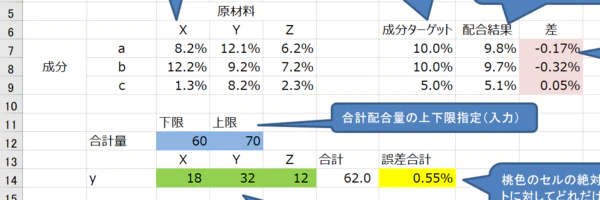
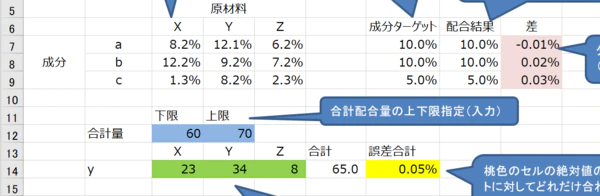
- 最適化楽屋話#14 Excelを使った数理最適化

更新日:2025年2月12日 18:19
公開日:2019年12月24日 09:00
※当記事は2019年7月に執筆・公開されたものです。
※「Numerical Optimizer」は2022年3月28日より「Nuorium Optimizer」に名称変更しております。
記事一覧
- 最適化楽屋話#1 数理最適化のテクニカルTips連載
- 最適化楽屋話#2 メタヒューリスティクスの登場
- 最適化楽屋話#3 杓子定規でない数理最適化の実現
- 最適化楽屋話#4 数理最適化でできること・できないこと
- 最適化楽屋話#5 実務家が数理最適化を行うセンス
- 最適化楽屋話#6 ポートフォリオ最適化問題
- 最適化楽屋話#7 Excelアドインによるレイバースケジューリング
- 最適化楽屋話#8 Excelアドインによるシフトスケジューリング
- 最適化楽屋話#9 Excelによる数理最適化サンプル
- 最適化楽屋話#10 数理最適化による生産スケジューリング
- 最適化楽屋話#11 Excelアドインによる配送計画サンプル
- 最適化楽屋話#12 ラインのディスパッチ問題の数理最適化モデル
- 最適化楽屋話#13 Excelアドインによる倉庫の在庫引き当て問題
- 最適化楽屋話#14 Excelを使った数理最適化
- 最適化楽屋話#15 数理科学手法の分類
- 最適化楽屋話#16 ウイルス感染拡大における数理最適化の貢献
- 最適化楽屋話#17 パンデミック時の数理的方法論による提案・論文
- 最適化楽屋話#18 Benders分解の概要
- 最適化楽屋話#19 電力施設・ネットワークの設備計画最適化
- 最適化楽屋話#20 ビジネスとして数理最適化を実践するために
- 最適化楽屋話#21 数理最適化のユースケース(イベントの質疑応答)